Reihe (Mathematik)

Eine Reihe, selten Summenfolge oder unendliche Summe und vor allem in älteren Darstellungen auch unendliche Reihe genannt, ist ein Objekt aus dem mathematischen Teilgebiet der Analysis. Anschaulich ist eine Reihe eine Summe mit unendlich vielen Summanden, wie etwa
Man kann Reihen als rein formale Objekte studieren, jedoch sind Mathematiker in vielen Fällen an der Frage interessiert, ob eine Reihe konvergiert, ob also die Summe endlich vieler Summanden durch Hinzunahme hinreichend vieler weiterer Summanden einem festen Wert beliebig nahe kommt. So konvergiert etwa die obige Beispielreihe gegen den Wert (siehe Bild), allerdings existieren auch divergente (also nicht konvergente) Reihen, wie zum Beispiel
Allgemein wird eine Reihe mit bezeichnet, und dies ist, falls existent, gleichzeitig die Bezeichnung für den Grenzwert.
Präzise wird eine Reihe als eine Folge definiert, deren Glieder die Partialsummen einer anderen Folge sind. Wenn man die Zahl 0 zur Indexmenge zählt, ist die -te Partialsumme die Summe der ersten (von den unendlich vielen) Summanden. Falls die Folge dieser Partialsummen einen Grenzwert besitzt, so wird dieser der Wert oder die Summe der Reihe genannt.
Eine systematische Theorie der Reihen findet ihren Ursprung im 17. Jahrhundert, wo sie besonders durch Gottfried Wilhelm Leibniz und Isaac Newton vorangetrieben wurde. Dabei stand sie in enger Verbindung zu anschaulichen Problemen aus der Geometrie, wie der Integration von Kurven. Als formale Objekte wurden Reihen im 18. Jahrhundert von Mathematikern wie Leonhard Euler studiert, der ihnen drei Bände seines Gesamtwerkes, der Opera Omnia, widmete. Erst im 19. Jahrhundert stieß dieser Umgang, der Fragen nach Konvergenz oder Divergenz außen vor ließ, auf Kritik. In einer wegweisenden Schrift aus dem Jahr 1821 schuf Augustin-Louis Cauchy die Grundlagen der bis heute gebräuchlichen „quantitativen“ Theorie unendlicher Reihen und bereitete der mathematisch strengen Aufarbeitung der Analysis, etwa durch Karl Weierstraß, den Weg. Von zentraler Bedeutung in diesem Zusammenhang war das Cauchy-Kriterium für die Charakterisierung des Konvergenzbegriffs. Bis in die heutige Zeit sind Reihen, etwa im Kontext der Zahlentheorie, ein Objekt intensiver mathematischer Forschung.
Für die Untersuchung einer unendlichen Reihe sind vor allen Dingen die Fragen nach ihrer Konvergenz und, wenn diese gegeben ist, nach dem Grenzwert von Bedeutung. Für beides existieren keine brauchbaren allgemeinen Methoden. Allerdings wurden Kriterien entwickelt, die in einigen Spezialfällen Antworten liefern.
Besonders bedeutende Anwendungen haben Reihen in der Analysis (zum Beispiel über Taylorreihen zu analytischen Funktionen), den Ingenieurwissenschaften (etwa in der Elektrotechnik und Signalverarbeitung über Fourierreihen), aber auch in der Wirtschaftswissenschaft und Finanzmathematik. Einige bedeutende mathematische Konstanten, etwa die Kreiszahl oder die Eulersche Zahl , konnten mit Hilfe von Algorithmen, die auf unendlichen Reihen fußen, auf viele Billionen Nachkommastellen angenähert werden.
Einführung
BearbeitenUnendliche Summierbarkeit und erste Beispiele
Bearbeiten
Unter einer Reihe versteht man, veranschaulicht, eine niemals endende Summe von Zahlen. Die Dezimalschreibweise einer reellen Zahl kann zum Beispiel als Reihe aufgefasst werden, etwa
oder auch mit der Kreiszahl :
- .
Die durch die Punkte angedeuteten Summen enden niemals, da die Dezimalentwicklung von periodisch und die Kreiszahl irrational ist. Es gibt Reihen, denen kein Wert zugeordnet werden kann, etwa
aber auch solche, die gegen einen Grenzwert konvergieren (wie die obigen Beispiele mit Grenzwerten bzw. ).
Darüber hinaus treten Reihen in vielen Bereichen der Mathematik auf und besitzen zahlreiche Anwendungsmöglichkeiten. Klassischerweise treten sie dann in Erscheinung, wenn mathematische Terme beliebig gut angenähert werden sollen oder die Entwicklung (theoretisch) nicht endender Prozesse analysiert wird. Auch in der Physik spielen Reihen eine wichtige Rolle. Eine einfache „Anwendung“ kann über das klassische Paradoxon von Achilles und der Schildkröte gegeben werden:[1]

Der für seine Schnelligkeit bekannte Heros Achilles liefert sich einen Wettkampf mit einer Schildkröte. Beide starten von der gleichen Position aus. Jedoch gewährt Achilles, der einhundert Mal schneller als die Schildkröte ist, dieser 100 Meter Vorsprung. Das Paradoxon besagt nun, dass Achilles die Schildkröte niemals einholen wird: Hat nämlich Achilles 100 Meter zurückgelegt, so hat sich die Schildkröte in der Zwischenzeit einen Meter von ihrer bisherigen Position weiter bewegt. Und läuft Achilles nun auch diesen weiteren Meter, so ist ihm die Schildkröte einen weiteren Zentimeter voraus. Und bewegt sich Achilles diesen Zentimeter, so hat die Schildkröte einen Zehntel Millimeter Vorsprung usw.
Das scheinbare Paradoxon entsteht dadurch, dass die Zeit nicht berücksichtigt wurde.[2] Genau genommen ist die Aussage, dass Achilles die Schildkröte niemals aufholen wird, nicht korrekt. Die in dem Paradoxon aufgeführten Zwischenschritte, in denen die Schildkröte stets einen rasch abnehmenden Vorsprung vor Achilles hat, sind allesamt mit Zeitabschnitten verbunden, die jedoch ebenso rasant abnehmen (zum Beispiel dann, wenn Achilles nur noch einen Zentimeter läuft). Brauchte Achilles für die ersten 100 Meter noch „eine Zeiteinheit“, so wird er für einen Meter nur noch „ Zeiteinheiten“ brauchen.[Anm. 1] Im nächsten Schritt braucht er für einen Zentimeter nur noch „ Zeiteinheiten“. Der Zeitpunkt, an dem Achilles und Schildkröte schließlich die gleiche Position haben werden, ist also, da deren Abstände immer weiter abnehmen, gegeben durch die unendliche Reihe
Obwohl also unendlich viele Terme addiert bzw. Zeitabschnitte betrachtet wurden, entsteht im Grenzwert eine endliche Zahl bzw. wird Achilles nach endlicher Zeit, nämlich nach Zeiteinheiten, die Schildkröte einholen.
Elementare Anwendungsbeispiele
BearbeitenDas Konzept der Reihe spielt disziplinübergreifend eine zentrale Rolle in der Mathematik. Hauptanwendungsgebiet ist zunächst die Analysis, jedoch auch alle durch diese Sparte beeinflussten Bereiche, nicht zuletzt angewandte Gebiete wie die Ingenieurwissenschaften.
Annäherung von Funktionen
BearbeitenReihen entfalten ihre Nützlichkeit zum Beispiel dann, wenn es darum geht, bestimmte Funktionen annähernd auszurechnen, die für Anwendungen zwar nützlich, aber dennoch kompliziert sind. Ein besonders berühmtes und zugleich wichtiges Beispiel ist die Darstellung der natürlichen Exponentialfunktion durch ihre Taylorreihe im Punkt :
wobei die Fakultät von bezeichnet. Bemerkenswert ist, dass sich jeder Term auf der rechten Seite durch die vier Grundrechenarten berechnen lässt, was auf nicht mehr zutrifft. Die Konstruktion dieser Reihe ist dadurch motiviert, dass die (termweise) Ableitung der rechten Seite die Reihe unverändert lässt und diese in den Wert 1 annimmt (was beides auch auf zutreffen „soll“). Für kleine Werte nähert sich diese Reihe relativ schnell dem Grenzwert an und ist dort für eine Berechnung durchaus geeignet. Neben der (punktweisen) Berechnungsmöglichkeit liefert diese Reihendarstellung auch erste Analysemöglichkeiten: Da für alle Terme positiv sind, ist erkennbar, dass die Exponentialfunktion für jede Art polynomiellen Wachstums übersteigen wird, da beliebig hohe Potenzen in der Summation auftreten.
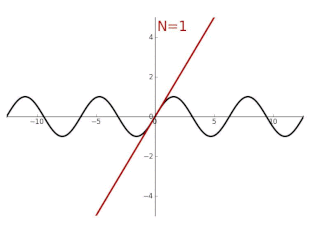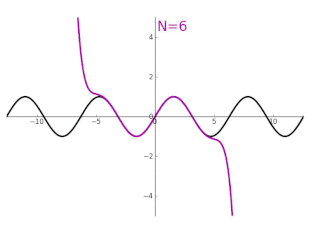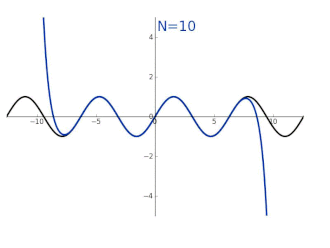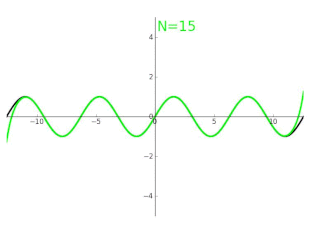
Ein weiteres Beispiel sind die Winkelfunktionen, etwa der Sinus. Es gibt auch hier kein einfaches, „geschlossenes“ Verfahren, für Eingabewerte den Ausgabewert zu berechnen, aber mittels Reihen können gute Näherungswerte relativ schnell berechnet werden, die in der Praxis ausreichen. Es gilt die Reihenentwicklung[3]
kurz:
Etwa ist und, wegen für alle , als Näherung bis zum -Term
Wahrscheinlichkeitstheorie
Bearbeiten
Bei der Untersuchung bestimmter Zufallsexperimente in der Wahrscheinlichkeitstheorie spielen Reihen eine wichtige Rolle. Ein einfaches Beispiel betrifft den „potenziell unendlichen Münzwurf“: Eine faire Münze wird dabei so oft geworfen, bis sie das erste Mal „“ (= Kopf) zeigt. Mit der anderen Möglichkeit „“ (= Zahl) gibt es damit folgende Möglichkeiten, wie das Experiment endet:
- usw.
Da sowohl als auch mit gleicher Wahrscheinlichkeit auftreten, und die Würfe unabhängig ablaufen, haben die zugehörigen Wahrscheinlichkeiten die Werte usw. Da aber gleichzeitig fast sicher irgendeines dieser Ereignisse eintreten muss, folgt
wobei die als die zum fast sicheren Ereignis gehörige Wahrscheinlichkeit („100 %“) zu interpretieren ist.[4] Die besondere Bedeutung der Theorie der Reihen in der Praxis wird in diesem Zusammenhang jedoch beim Übergang zu Erwartungswerten ersichtlich. Um dies zu sehen, hilft es, das obige Experiment als ein Glücksspiel zu deuten, bei dem zum Beispiel stets die Zahl an Euro ausgezahlt wird, die angibt, wie oft „Zahl“ geworfen wurde (also zum Beispiel 3 Euro bei ZZZK) – zu Beginn aber eine Gebühr von 2 Euro verlangt wird. Es muss der Gewinn stets mit der zugehörigen Wahrscheinlichkeit gewichtet werden, und somit beträgt der zu erwartende Gewinn
pro Runde.[5] Die Teilnahme an diesem Glücksspiel ist demnach nicht zu empfehlen, da der Spieler pro Runde durchschnittlich 1 Euro verlieren wird. Für die Grenzwertermittlung der Reihe, die nicht ganz einfach ist, werden Methoden aus der Analysis herangezogen.
Definition und Grundlagen
BearbeitenBegriff
BearbeitenEine Reihe wird selten Summenfolge[6] oder unendliche Summe[7][8] und vor allem in älteren Darstellungen auch unendliche Reihe genannt.[9]
Für reelle und komplexe Folgen
BearbeitenIst eine beliebige reelle (oder komplexe) Folge gegeben ( ist die Menge der nichtnegativen ganzen Zahlen und bezeichnet die „ist-Element-von“-Relation), kann man aus ihr eine neue Folge der Partialsummen bilden. Die -te Partialsumme ist die Summe der ersten Glieder von , ihre Definition lautet:
Die Folge der -ten Partialsummen heißt Reihe.
Zu bemerken ist, dass aus der Definition folgt, dass andersherum jede Zahlenfolge zu einer Reihe wird, wenn man diese als Partialsummen der Folge auffasst. Eine Reihe ist also nichts anderes als eine Folge spezieller „Bauart“, deren Glieder rekursiv durch und definiert sind. Allerdings führt die einfache rekursive Struktur der Reihen zu vergleichsweise sehr handlichen Konvergenzkriterien, siehe unten.[10]
Konvergenz und Divergenz
BearbeitenObwohl Reihen auch als formale Objekte studiert werden können, also „ohne Wert“, sind in der Mathematik die Fälle von besonderem Interesse, in denen sich die Reihe langfristig einem ganz bestimmten Wert annähert. Falls die Reihe , also die Folge der Partialsummen
- ( ist das Summenzeichen)
konvergiert, so nennt man ihren Grenzwert
den Wert der Reihe[11] oder die Summe der Reihe.[12] Dieser ist eindeutig bestimmt und wird meistens als notiert.[10][Anm. 2] Reihen, die nicht konvergieren, nennt man divergent.

Anschaulich bedeutet Konvergenz, dass sich eine Folge auf Dauer einer reellen oder komplexen Zahl beliebig nah annähert. Da der Umgang mit „dem Unendlichen“ zunächst nicht sinnvoll ist, umgeht man diese Schwierigkeit, indem man den Konvergenzbegriff mit endlichen Mitteln erklärt. Die Reihe nennt man dann konvergent gegen den Grenzwert , wenn es zu jeder noch so kleinen Zahl einen Index gibt, sodass für alle noch größeren Indizes
erfüllt ist. Hat eine Reihe etwa den Grenzwert , so besagt die Wahl , dass alle bis auf endlich viele Partialsummen
zwischen und liegen. Ebenso lässt sich mit – ab einem gewissen Index liegen also alle Partialsummen zwischen und – usw. verfahren. In manchen Fällen ist dieses Kriterium für Konvergenz jedoch nicht brauchbar, da bereits ein Grenzwert bekannt sein muss, um es überhaupt anwenden zu können. Es ist im Allgemeinen jedoch überaus schwierig, den Grenzwert einer konvergenten Reihe anzugeben. Dies kann aber leicht umgangen werden, denn eine Reihe konvergiert genau dann, wenn es für jede Zahl einen Index gibt, sodass für alle größeren Indizes bereits
gilt.[13] Man bezeichnet dies als das Cauchy-Kriterium, und es kommt ohne Verwendung eines expliziten Grenzwertes aus. Allerdings eignet sich das Cauchy-Kriterium im Rahmen praktischer Konvergenztests von Reihen eher selten. Hierfür sind speziellere, aber dafür leichter handzuhabende Kriterien entwickelt worden, die jedoch nicht allgemeingültig sind (siehe unten). Häufigere Anwendung findet das Cauchy-Kriterium aber innerhalb mathematischer Beweise, etwa wenn aus der Konvergenz einer Reihe eine Schlussfolgerung gezogen werden soll. Ein erstes Beispiel ist die Aussage, dass aus der Konvergenz einer Reihe bereits für folgt, also dass die Folge der Summanden eine Nullfolge bildet. In der Tat, ist beliebig gewählt, folgt mit dem Cauchy-Kriterium, angewandt auf den „Ein-Summand“-Spezialfall schon
- für alle .
Damit muss gegen 0 konvergieren. Zu beachten ist, dass die Rückrichtung dieser Aussage nicht richtig ist, da die Betrachtung einzelner Summanden im Allgemeinen keine wirkungsvollen Rückschlüsse auf ganze Summen zulässt. Dies ist einer der Gründe schlechthin, weshalb die Theorie der unendlichen Reihen so schwierig ist.
In manchen Fällen müssen auch Reihen der Form untersucht werden. Diese heißen konvergent genau dann, wenn die beiden Reihen
konvergieren.[14]
Hinsichtlich divergenter Reihen ist zu beachten, dass das Phänomen der Divergenz keinesfalls mit der Unbeschränktheit der Partialsummen gleichzusetzen ist. So existieren divergente Reihen, deren Partialsummen beschränkt sind, zum Beispiel
Das Themenfeld der Reihenkonvergenz ist bis heute ein schwieriges Gebiet, und es gibt kein allgemeingültiges und zugleich brauchbares Kriterium, um schnell zu entscheiden, ob eine vorgelegte Reihe konvergiert oder divergiert. Ein Grund hierfür ist, dass es keinen „klaren Übergang“ zwischen Konvergenz und Divergenz gibt. So existiert etwa keine „am langsamsten konvergierende Reihe“, und ebenso keine „am langsamsten divergierende Reihe“.[15] Ist etwa mit einer Nullfolge konvergent, so auch , und letztere Reihe konvergiert langsamer als die vorherige. Darüber hinaus zeigte Alfred Pringsheim, dass die Glieder einer konvergenten Reihe keinesfalls mit einer „Mindestgeschwindigkeit“ gegen streben müssen. Es kann sogar jede konvergente Reihe für einen Beweis dieser Behauptung herangezogen werden.[16]
Bedingte und absolute Konvergenz
Bearbeiten
Es gibt unterschiedliche Arten der Konvergenz. Dies betrifft nicht die Konvergenzdefinition, die stets dieselbe ist, sondern die „Güte“ der Konvergenz. So kann man zwei Typen konvergenter Reihen angeben: jene, die gewissermaßen „stabil“ konvergieren, und solche, bei denen größere Vorsicht zum Nachweis einer Konvergenz geboten ist, etwa bei der Umordnung von Summanden innerhalb der Reihe.
Eine Reihe heißt absolut konvergent, wenn auch die zugehörige Reihe der Absolutbeträge konvergiert. Darin ist die Betragsfunktion.
Durch das Summieren der Beträge werden alle möglichen Vorzeichen bzw. Ausrichtungen der quasi „ignoriert“, was den Nachweis einer Konvergenz erschwert, da dann kein „Wegkürzen“ mehr möglich ist. Etwa ist die alternierende Reihe
konvergent, nicht aber die harmonische Reihe
Es ist ein erstes Beispiel einer bedingt konvergenten Reihe, also einer, die nicht absolut konvergiert.[17] Zudem zeigt das Beispiel der harmonischen Reihe, dass die Eigenschaft der Glieder, eine Nullfolge zu sein, nicht ausreicht, um Konvergenz zu erreichen. Es lässt sich das Nullfolgenkriterium also nicht umkehren.
Aus mathematischer Sicht ist absolute Konvergenz ein Vorteil, da diese das Rechnen mit Reihen vereinfacht. Hintergrund dessen ist, dass sich bei absolut konvergenten Reihen kanonisch die Dreiecksungleichung verwenden lässt, was in vielen Fällen verhältnismäßig einfache Schlussfolgerungen ermöglicht. Etwa ist es im Falle bedingter Konvergenz nicht ohne Weiteres erlaubt, die Reihenfolge der Summanden zu ändern, ohne dabei möglicherweise den Grenzwert zu verändern. Damit entfällt bei bedingt konvergenten Reihen das noch für endliche Summen gültige Kommutativgesetz. Im Gegensatz dazu ist es bei absolut konvergenten Reihen unerheblich, in welcher Reihenfolge summiert wird, da der Grenzwert stets derselbe bleibt.[18] Dies kann wie folgt gesehen werden:[19] Ist absolut konvergent und eine Bijektion, so findet man zu ein mit
- für alle .
Ist nun groß genug, beinhaltet die Menge . Dann gilt für alle mit der Dreiecksungleichung
Mit folgt insgesamt, wieder mit der Dreiecksungleichung,
- für alle
Zusätzlich besagt der Riemannsche Umordnungssatz, dass bei einer bedingt konvergenten Reihe mit reellen Gliedern durch Umordnungen jede reelle Zahl als Grenzwert und auch die Divergenz der neu entstehenden Reihe erzwungen werden kann.
Die absolute Konvergenz kann auch auf Multireihen ausgedehnt werden.[20] Konvergiert für jedes , und konvergiert , dann konvergieren die Reihen
- für jedes ,
- für jedes ,
und es gilt
- .
Geschichte
BearbeitenAnfänge im 17. Jahrhundert
Bearbeiten
Reihen wurden in der Mathematik hauptsächlich eingeführt, um geometrische Probleme zu lösen. Ihre zunächst eher sporadische Verwendung gewann um 1650 an Bedeutung und war zum Beispiel entscheidend für die Entstehung der Infinitesimalrechnung. Besonders zu Zeiten von Isaac Newton und Gottfried Wilhelm Leibniz wurden viele Ergebnisse erzielt, und ein großer Teil des frühen Wissens um die Reihen geht auf sie zurück.[21]
Obwohl Reihen schon früher gelegentlich vorkamen, wurden sie in der Mathematik erst ab dem 17. Jahrhundert wirklich bedeutsam. Ihre Verwendung erfolgte vor allem im Zusammenhang mit dem Problem der Quadratur und der Abmessung von Kurven durch Einteilung in lineare Segmente (siehe auch Rektifizierbarkeit). Im 17. Jahrhundert versuchten die Mathematiker, neue Methoden für die Quadratur gekrümmter Linien zu finden, die die Schwierigkeiten der sogenannten Exhaustionsmethode vermeiden.[22]
Der Geistliche und Mathematiker Pietro Mengoli veröffentlichte 1650 in seinem Werk Novae quadraturae arithmeticae, seu de additione fractionum Resultate bezüglich unendlicher Reihen und baute seine Argumente auf zwei Axiome auf.[23] Unter anderem fand er die Grenzwerte:[24]
Ferner fragte er nach dem Grenzwert der Reihe
blieb bei dessen Suche aber erfolglos. Dieses Problem wurde später von Jakob Bernoulli aufgegriffen, und schließlich als Basler Problem bekannt. Erst Leonhard Euler fand den korrekten Grenzwert mit der Kreiszahl im Jahr 1735 und veröffentlichte ihn in seinem Werk De Summis Serierum Reciprocarum.[25]

Im Jahr 1666 verfasste Newton eine Schrift De Analysi per Aequationes Numero Terminorum Infinitas, die zwar erst 1711 publiziert wurde, aber zuvor in Manuskriptform Wellen schlug. In dieser entwickelte er das heute als Newtonverfahren bekannte Prinzip, Nullstellen einer Funktion numerisch anzunähern. Er betrachtete den Spezialfall analytischer Funktionen, und es gibt nirgends einen Hinweis darauf, dass er das Verfahren auf geometrische Weise erhalten hat. Er wandte diese Technik auf die Umkehrung von Reihen an und gewann unter anderem dadurch die Reihenentwicklungen für Sinus und Kosinus.[26] Inspiriert durch das von John Wallis verfasste Werk Arithmetica infinitorum entdeckte er zudem die allgemeine Binomialreihe, in heutiger Notation
die sich zur numerischen Annäherung von Wurzeln eignet. Dies geht aus einem Brief von Newton an Leibniz aus dem Jahre 1676 hervor.[27] Newton hat für sein Theorem jedoch nie einen Beweis geliefert, denn für ihn gab es genug numerische und experimentelle Evidenz.[28]
Fast zur gleichen Zeit, ab 1672, befasste sich Gottfried Wilhelm Leibniz mit der Theorie der unendlichen Reihen. Diese spielte eine wichtige Rolle bei seinen späteren Beiträgen zum Aufbau der Infinitesimalrechnung.[29] Leibniz untersuchte Reihen oft mit einer geometrischen Fragestellung oder Anschauung; Beispiele hierfür sind seine Behandlung der geometrischen Reihe[30] und der berühmten Leibniz-Reihe
die er über die Geometrie des Kreises erklärte.[31]
18. Jahrhundert
Bearbeiten
Im Laufe des 18. Jahrhunderts wurde die hauptsächlich von den gegenseitigen Widersachern Newton und Leibniz initiierte Theorie der unendlichen Reihen systematisch ausgebaut. Einen ersten Höhepunkt erlebte sie durch das Werk Methodus incrementorum von Brook Taylor, das 1715 veröffentlicht wurde. Darin entwickelte Taylor die heute nach ihm benannte Taylorreihe
systematisch, also die Möglichkeit, eine hinreichend gutartige Funktion anhand all ihrer Ableitungen in einem Punkt in Umgebung dieses Punktes zu rekonstruieren. Dabei bezeichnet die -te Ableitung der Funktion im Punkt und die Fakultät von . Dieser Ansatz war bereits Newton bekannt gewesen, jedoch hatte er diesbezüglich nur kurze Ausführungen geliefert und es bleibt unklar, ob er die Wichtigkeit der Potenzreihen richtig einschätzte.[32] Diese wurde in den folgenden Jahren jedoch zunehmend erfasst. Abraham de Moivre bewies einen Satz über Potenzreihen zu rekursiven Folgen und erkannte, wie andere Mathematiker dieser Zeit, dass diese eng mit sogenannten charakteristischen Polynomen der entsprechenden Rekursion zusammenhingen. Etwa gab Daniel Bernoulli 1728 mit deren Hilfe eine geschlossene Formel für die sonst nur über eine Rekursion definierte Fibonacci-Folge an.[33]
James Stirling argumentierte in seiner 1730 publizierten Methodus differentialis, dass langsam konvergente Reihen „ebenso unnütz“ wie divergente Reihen seien, und stellte Verfahren vor, um die Konvergenz gewisser Reihen zu beschleunigen.[34] Diese sollten auch dazu dienen, die Werte gewisser endlicher Summen schnell ausrechnen oder zumindest approximieren zu können. Unter seinen Entdeckungen fand sich auch die nach ihm benannte Stirlingformel, welche die Fakultät einer natürlichen Zahl über einen asymptotischen Reihenausdruck sehr schnell für große annähert.[35] Die 1742 von Colin Maclaurin veröffentlichte und zeitgleich auch von Leonhard Euler entdeckte und genutzte Euler-Maclaurin-Formel, die die Arbeiten von Newton zur geometry of fluxions aufgriff,[36] ging in eine ähnliche Richtung.[37] Mit ihrer Hilfe konnte Maclaurin neue Beweise zu Aussagen von Newton und Stirling über Taylorreihen anfertigen und die Reihenkonvergenz durch seinen neuartigen Zugang in einigen Fällen beschleunigen.[38]

Besonders wichtige Beiträge zur Theorie der Reihen lieferte jedoch Leonhard Euler. Sie galten als eines seiner Lieblingsthemenfelder, und alleine drei Bände seiner Opera Omnia sind ihnen gewidmet.[39] Zahlreiche bedeutende Entdeckungen Eulers fußen letztlich auf seiner Intuition. Darunter fallen seine Verallgemeinerung der Fakultät über die Gammafunktion,[40] die Lösung des Basler Problems und zahlreiche weitere gefundene Grenzwerte bestimmter Reihen, wie etwa[41]
- (die Nenner sind „perfekte Quadrate minus 1, die selbst auch andere Potenzen sind“, etwa usw.)[42]
sowie seine Entdeckung der Euler-Maclaurin-Formel im Jahr 1732 (Beweis 1736).[43] Euler zog praktischen Nutzen aus dieser Formel, um unendliche Reihen, die langsam konvergieren, schnell numerisch anzunähern. So gab er gute Näherungen für die Werte und , wobei die Riemannsche Zeta-Funktion bezeichnet, und fand auf 20 Stellen genau:
Erwiesenermaßen etablierte Eulers ursprüngliche Methode der Berechnung von für höhere Werte von die numerische Mathematik als ein neues Forschungsgebiet.[44] Neuartig war auch sein Zugang zur Zahlentheorie über unendliche Reihen. Mit dem sog. Satz von Euler zeigte er, dass
gilt und deutete sein Resultat dahingehend, dass Primzahlen dichter in den natürlichen Zahlen liegen müssten als Quadratzahlen. Es war zudem Euler, der als erster divergente Reihen systematisch untersuchte.[45] Dabei entging Euler jedoch keinesfalls die Problematik, welche die Zuweisung eines Summenwertes zu einer divergenten Reihe mit sich bringen konnte. So hatte schon Guido Grandi aus
- „“
die Gleichheit abgeleitet, und damit die Möglichkeit der Erschaffung der Welt aus dem Nichts „bewiesen“. Später bemerkte man weitere Widersprüche, die durch das unbedarfte Rechnen mit divergenten Reihen entstehen können.[46] Obwohl Euler für seinen Umgang mit divergenten Reihen kritisiert wurde, wird sein intuitiver Zugang bis heute anerkannt. So konnte er einige korrekte Resultate mit dessen Hilfe entdecken, und seine Intuition nahm Ideen aus der Theorie der Limitierungsverfahren, die den Umgang mit divergenten Reihen ab dem 19. Jahrhundert systematisch formalisierte, vorweg.[47]
Nach 1760 entwickelte sich die Theorie der unendlichen Reihen schließlich maßgeblich in die Richtung, die Euler vorgegeben hatte. Der formale Zugang (es wurden etwa Fragen der Konvergenz oft ignoriert, und Terme wurden abstrakt umgeformt) bereitete vielen bemerkenswerten Resultaten den Boden, etwa der Lagrangeschen Inversionsformel, 1768 gezeigt von Joseph-Louis Lagrange in seiner Nouvelle méthode pour résoudre les équations littérales par le moyen des séries,[48] und der Theorie erzeugender Funktionen von Pierre-Simon Laplace.[49] Im Jahr 1797 konnte Lagrange schließlich die Theorie der analytischen Funktionen konstruieren mit dem Ziel, die Differentialrechnung rein durch formale Betrachtungen aufzubauen.[50]
19. Jahrhundert
Bearbeiten
Zu Beginn des 19. Jahrhunderts stieß die formale Herangehensweise an die Theorie der unendlichen Reihen, also etwa jenseits von Fragen der Konvergenz, zunehmend auf Ablehnung. Ziel war es, zu einem „quantitativen Verständnis“ von Reihen zu gelangen. Die erste Arbeit in diese Richtung stammt von Carl Friedrich Gauß aus dem Jahr 1813. Zuvor hatte Joseph Fourier bereits Reihen trigonometrischer Funktionen untersucht, dabei aber einen anderen Ansatz gewählt als vorher Euler und Lagrange. Schließlich gab Augustin-Louis Cauchy die erste systematische Abhandlung eines rein quantitativen Zugangs zur Theorie der Reihen im Jahr 1821. Ein wesentlicher Grund, weshalb die formale Herangehensweise nicht mehr breite Akzeptanz fand, war, dass sie an einen Punkt gelangt war, an der die Analysis nicht weiter wachsen konnte.[51] Cauchy erklärte dazu:
„Was die Methoden anbelangt, so habe ich mich bemüht, ihnen die ganze Strenge zu geben, die man in der Geometrie braucht, um niemals auf die Argumente zurückgreifen zu müssen, die aus der Allgemeinheit der Algebra stammen. Derartige Begründungen, die zwar allgemein anerkannt sind, insbesondere beim Übergang von konvergenten zu divergenten Reihen und von reellen Größen zu imaginären Ausdrücken, können, wie mir scheint, nur manchmal als Induktionen betrachtet werden, die geeignet sind, die Wahrheit darzustellen, die aber wenig geeignet sind, die in den mathematischen Wissenschaften so gepriesene Exaktheit zu erreichen. Gleichzeitig muss man feststellen, dass sie dazu neigen, den algebraischen Formeln eine unbestimmte Ausdehnung zuzuschreiben, während in Wirklichkeit der größte Teil dieser Formeln nur unter bestimmten Bedingungen und für bestimmte Werte der in ihnen enthaltenen Mengen existiert. Indem ich diese Bedingungen und Werte bestimme und den Sinn der von mir verwendeten Bezeichnungen genau festlege, lasse ich jede Ungewissheit verschwinden; und dann handelt es sich bei den verschiedenen Formeln um nichts anderes als um Beziehungen zwischen reellen Größen, Beziehungen, die immer leicht zu überprüfen sind, wenn man die Größen selbst durch Zahlen ersetzt. Um diesen Prinzipien treu zu bleiben, war ich zugegebenermaßen gezwungen, mehrere Vorschläge zu akzeptieren, die auf den ersten Blick etwas hart erscheinen. Zum Beispiel: Eine divergente Reihe hat keine Summe.“
Im weiteren Verlauf verlagerte sich der Forschungsschwerpunkt entsprechend auf den „quantitativen Umgang“ mit Reihen, der sich in vielerlei Hinsicht als schwieriger und gleichzeitig fruchtbarer erwies. So kam die Frage nach Kriterien auf, wie man entscheiden könnte, ob eine unendliche Reihe überhaupt konvergiert. Beiträge in diese Richtung stammen unter anderem von Niels Henrik Abel, Augustin-Louis Cauchy, Peter Gustav Lejeune Dirichlet und Carl Friedrich Gauß. In dieser Zeit machten sich auch Cauchy und Karl Weierstraß um den Aufbau der modernen Funktionentheorie verdient. Besonders Weierstraß verwendete dafür systematisch eine moderne, bis heute gebräuchliche Theorie der Potenzreihen.[53] In seinem 1859 verfassten Artikel Über die Anzahl der Primzahlen unter einer gegebenen Grösse.[54] nutzte Bernhard Riemann diese „strenge“ Funktionentheorie, um Primzahlen zu untersuchen. Die Schwierigkeit lag darin, der Reihe
auch außerhalb ihres Konvergenzbereichs einen „quantitativen Sinn“ zu geben.[55] Zuvor hatte Euler ebenfalls diese sogenannte Zeta-Funktion studiert, jedoch nur als formales Objekt und nicht über den komplexen Zahlen, weshalb ihm strenge Beweise, etwa für ihre Funktionalgleichung, verwehrt geblieben waren. Auch wurden die Unterschiede zwischen bedingter und absoluter Konvergenz herausgearbeitet. So zeigte Riemann im Jahr 1866 den Riemannschen Umordnungssatz.[56] Auch konnten mit Hilfe der Reihen pathologische Beispiele in der Analysis konstruiert werden. Karl Weierstraß zeigte 1872, dass die Weierstraß-Funktion
- , mit und mit
in zwar überall stetig, aber nirgends differenzierbar ist.[57]
Die Theorie der divergenten Reihen wurde jedoch nicht gänzlich verworfen. War sie von Cauchy und Abel noch als „Erfindung des Teufels“ gebrandmarkt worden, lieferte ironischerweise der Abelsche Grenzwertsatz einen Grundstein für eine moderne und widerspruchsfreie Theorie der Limitierungsverfahren divergenter Reihen, die ab der zweiten Hälfte des 19. Jahrhunderts von Émile Borel und Ferdinand Georg Frobenius vorangetrieben wurde.[58]
20. Jahrhundert bis heute
BearbeitenIm Laufe des 20. Jahrhunderts wurde unter anderem eine „strenge“ Theorie der divergenten Reihen, unter Vorbehalt gewisser Voraussetzungen, aufgebaut. Bei diesen Limitierungsverfahren wird, unter Berücksichtigung des quantitativen Verständnisses von Reihen, durch Limesbildung der Konvergenzbegriff verallgemeinert, sodass die Klasse „konvergenter Reihen“ ausgedehnt wird.[59] Der Autodidakt Srinivasa Ramanujan hatte 1910 unter anderem durch die Behauptung

- „“
für Aufmerksamkeit gesorgt, wobei neben weitestgehender Ablehnung (wegen der offensichtlichen Divergenz der Reihe zur linken Seite) der Brite Godfrey Harold Hardy darin eine korrekte „Auswertung“ des Funktionswertes mit der Riemannschen Zeta-Funktion wiedererkannte (siehe auch Summe aller natürlichen Zahlen). Ramanujan hatte, ähnlich wie Leonhard Euler, eine gute Intuition für Limitierungsverfahren gehabt, und damit einige tiefgreifende Resultate vorhergesagt, ohne dafür strenge Beweise anzugeben.[60] Zu seinen zahlreichen Entdeckungen gehörten Reihenformeln wie[61]
und auch[62]
Dabei bezeichnen und den Sinus hyperbolicus, Cosinus hyperbolicus, Kotangens und den Kotangens hyperbolicus, bezeichnet die Eulersche Zahl.
Der Ramanujanexperte Bruce Berndt wies darauf hin, dass unter den Veröffentlichungen im 20. Jahrhundert, die durch Ramanujan vorhergesagte Formeln im Nachhinein bewiesen, ein Großteil zum Thema der unendlichen Reihen gehörte.[63]
Konvergenzklassen in der Theorie der Limitierungsverfahren wurden als unterschiedlich groß erkannt. Zum Beispiel zeigte bereits Abel, dass, falls konvergiert, auch der Grenzwert
existieren muss. Die Umkehrung dieses Resultats ist jedoch nicht richtig: Es existieren Reihen, die sich im obigen Sinne limitieren lassen mit divergenter Reihe . Das Resultat Abels, das also eine Konvergenzklasse, nämlich die „klassische Konvergenz“, in eine größere Klasse einbettet, ist Spezialfall eines Abelschen Theorems. Sätze, die hinreichende Bedingungen für Umkehrungen von Abelschen Sätzen herausarbeiten, wurden durch Arbeiten von Alfred Tauber initiiert.[64] Tauber zeigte, dass, falls existiert und , die Reihe konvergieren muss. Die sogenannten Tauber-Theoreme spielen bis heute in der Zahlentheorie, etwa beim Beweis des Primzahlsatzes, eine bedeutende Rolle.[65] Besonders Godfrey Harold Hardy und John Edensor Littlewood griffen die Ideen Taubers auf und verallgemeinerten sie. Im Jahr 1949 erschien Hardys Buch mit dem Titel Divergent Series.[66]
Auch in der Theorie der Fourierreihen wurden weitere Erfolge erzielt. 1923 konstruierte Andrei Nikolajewitsch Kolmogorow eine -integrable Funktion, deren Fourierreihe fast überall divergiert.[67] Dies widersprach Vermutungen seines Lehrers Nikolai Nikolajewitsch Lusin, der die punktweise Konvergenz solcher Fourierreihen vermutete. Für quadratintegrable Funktionen (Klasse ) vermutete man ebenfalls lange, dass sich Gegenbeispiele finden lassen würden, bis Lennart Carleson 1966 Lusins Vermutung für diese Klasse bewies.[68]
Im weiteren Verlauf des 20. Jahrhunderts wurden Reihen verstärkt auch in formalen algebraischen Rahmen, also jenseits von Konvergenzfragen, als abstrakte Strukturen untersucht. So formen etwa die formalen Potenzreihen mit Koeffizienten in einem Ring zusammen mit komponentenweiser Addition und dem Cauchyprodukt einen Ring .[69] Häufig wird die Wahl getroffen. In diesem Fall ist sogar faktoriell.[70] Im Jahr 1959 konnten E. D. Cashwell und C. J. Everett zeigen, dass der Ring der formalen Dirichletreihen isomorph zu einem Potenzreihenring mit abzählbar vielen Veränderlichen, und damit insbesondere faktoriell, ist.[71] Ferner erwies sich der „algebraische“ Umgang mit Reihen auch für die Kombinatorik von großem Nutzen. Diese Initiative wurde unter anderem von George Andrews seit den 1970er Jahren vorangetrieben, der zahlreiche kombinatorische Fragen, etwa zu den Partitionen, durch Reihenumformungen beantworten konnte, und an einem systematischen Ausbau der Theorie sogenannter „-Reihen“ maßgeblich beteiligt war.[72][73] Allerdings waren derartige Ansätze bereits zu den Zeiten Leonhard Eulers bekannt, der unter anderem den Pentagonalzahlensatz bewies.[74]
Bis zum heutigen Tage sind Konvergenzfragen von Reihen von höchster Bedeutung und keinesfalls gelöst. So wird etwa die Riemannsche Vermutung, eines der sieben Millennium-Probleme, auf dessen Lösung der Preis von 1 Million US-Dollar ausgesetzt ist, von der Konvergenz der Reihe
für alle Werte impliziert.[75] Dabei hängt die Möbiusfunktion eng mit der Verteilung der Primzahlen zusammen. Bis dato ist lediglich Konvergenz für und die Tatsache
bekannt, was äquivalent zum Primzahlsatz ist.[76]
Rechnen mit Reihen
BearbeitenIm Gegensatz zu gewöhnlichen (endlichen) Summen gelten für Reihen einige übliche Regeln der Addition nur bedingt. Man kann also nicht bzw. nur unter bestimmten Voraussetzungen mit ihnen wie mit endlichen Summenausdrücken rechnen. Es stellen sich grundsätzlich die Fragen:
- Wie kann man Reihen addieren, und wie wirkt sich das auf Konvergenz und Grenzwerte aus?
- Wie kann man Reihen multiplizieren, und wie wirkt sich das auf Konvergenz und Grenzwerte aus?
Summen und Vielfache
BearbeitenMan kann konvergente Reihen gliedweise addieren, subtrahieren oder mit einem festen Faktor (aber nicht einer anderen Reihe) multiplizieren (vervielfachen). Die resultierenden Reihen sind ebenfalls konvergent, und ihr Grenzwert ist die Summe bzw. Differenz der Grenzwerte der Ausgangsreihen bzw. das Vielfache des Grenzwertes der Ausgangsreihe. D. h.:
- .[77]
Produkte
BearbeitenMan kann absolut konvergente Reihen gliedweise miteinander multiplizieren. Die Produktreihe ist ebenfalls absolut konvergent und ihr Grenzwert ist das Produkt der Grenzwerte der Ausgangsreihen. D. h.:[78]
Da die Schreibweise (auf der linken Seite der Gleichung) der Produktreihe mit zwei Indizes in bestimmten Zusammenhängen „unhandlich“ ist, wird die Produktreihe auch in Form des Cauchyprodukts geschrieben. Der Name ergibt sich daraus, dass die Glieder der Produktreihe mit Hilfe des Cauchyschen Diagonalverfahrens gebildet werden, dabei werden die Glieder der Ausgangsfolgen in einem quadratischen Schema paarweise angeordnet, und die (durchnummerierten) Diagonalen dieses Schemas bilden die Produktglieder. Für die Produktreihe braucht man dann nur noch einen einzelnen Index. Die Produktreihe hat dann die folgende Form:
Der Satz von Mertens besagt, dass das Produkt beider Reihen und auch noch dann gegen das Produkt der Grenzwerte konvergiert, wenn mindestens eine der beiden Reihen absolut konvergiert.[79] Es konvergiert die Reihe mit genau dann für alle konvergenten , falls absolut konvergiert.[80]
Anwendungen haben Reihenprodukte zum Beispiel beim Nachweis von Funktionalgleichungen. Setzt man etwa
so konvergiert die betroffene Reihe für alle absolut. Mit dem binomischen Lehrsatz erhält man für und :
Damit folgt mit dem Cauchyprodukt für alle
was die Funktionalgleichung der Exponentialfunktion ist.[81]
Rechnen innerhalb der Reihe
BearbeitenKlammerung (Assoziativität)
BearbeitenMan kann innerhalb einer konvergenten Reihe die Glieder beliebig durch Klammern zusammenfassen. Man kann also beliebig viele Klammern in den „unendlichen Summenausdruck“ einfügen, man darf sie nur nicht innerhalb eines (aus mehreren Termen zusammengesetzten) Gliedes setzen. Der Wert der Reihe ändert sich durch die zusätzlich eingefügte Klammerung dann nicht.
Dies gilt für divergente Reihen im Allgemeinen nicht, was man leicht am folgenden Beispiel erkennt: Die Reihe
divergiert, während die beklammerte Reihe
gegen Null konvergiert und die anders beklammerte Reihe
gegen noch eine andere Zahl konvergiert.[82]
Andererseits kann man aber keine Klammern ohne Weiteres weglassen. Man kann das aber immer dann, wenn die resultierende Reihe wieder konvergent ist. In diesem Falle bleibt auch der Reihenwert unverändert: Sind die Glieder einer konvergenten Reihe selbst in Summenform (mit und ), so „darf“ man die sie umschließenden Klammern genau dann weglassen, wenn die dadurch entstehende neue Reihe wieder konvergiert.[82]
Umordnung (Kommutativität)
BearbeitenEine Umordnung einer Reihe wird durch eine Permutation ihrer Indexmenge dargestellt. Ist die Indexmenge zum Beispiel die Menge der natürlichen Zahlen mit Null und eine bijektive Abbildung der natürlichen Zahlen auf sich, so heißt
eine Umordnung der Reihe[83]
Man kann konvergente Reihen unter Beibehaltung ihres Wertes dann und nur dann beliebig umordnen, wenn sie unbedingt bzw. absolut konvergent sind. Es gilt für unbedingt (oder absolut) konvergente Reihen:
- für alle bijektiven .
Bedingt konvergente Reihen dürfen zur Erhaltung des Grenzwerts nur endlich umgeordnet werden, d. h. ab einem gewissen Index muss für die Umordnung gelten. Der Riemannsche Umordnungssatz sagt aus, dass durch geeignete Umordnung einer fixierten, bedingt konvergenten Reihe reeller Zahlen jeder reelle Grenzwert erreicht werden kann.[84]
Reihen von Funktionen
BearbeitenAllgemeines
BearbeitenEin zentrales Problem der Analysis besteht darin, „komplizierte“ Funktionen zu studieren. Dabei bedeutet „kompliziert“ zum Beispiel, dass die Rechenvorschrift nicht aus einer endlichen Abfolge aus Anwendungen der vier Grundrechenarten besteht. Eine in diesem Sinne „einfache“ Vorschrift wäre: Nimm die Eingangszahl mal Zwei, dann das Ergebnis plus Eins, multipliziere dies mit sich selbst, teile dann alles durch die Drei. In Kurzform: . Jedoch lassen sich sehr viele Phänomene in der Natur nicht so einfach beschreiben. Die Mathematik ist demnach bestrebt, Analyseverfahren nichttrivialer Funktionen zu entwickeln. Solche Verfahren kommen in den unterschiedlichsten Bereichen innerhalb der Mathematik und auch ihrer Anwendungen zum Einsatz.

Eine naheliegende Möglichkeit, „komplizierte“ Funktionen zu konstruieren und untersuchen, ist, sie als Reihe von Funktionen zu schreiben, wobei jeder einzelne Summand in der Praxis „einfache Eigenschaften“ besitzt:[85]
Anstatt also Folgen von Zahlen kann man auch Folgen von Funktionen betrachten und entsprechend Reihen definieren. Zudem ist zu beachten, dass im Darstellungsbereich alle notwendigerweise an allen Stellen aus dem Definitionsbereich von definiert sein müssen. Ferner muss im Zielbereich der Funktionen die Addition von Termen definiert sein, da sonst keine sinnvolle Reihe gebildet werden kann.
Eigenschaften der Grenzfunktionen
BearbeitenIm Falle der Konvergenz einer Funktionenreihe kommt noch die Frage nach den Eigenschaften der Grenzfunktion auf. Meistens wird gefragt: „Falls die einzeln betrachtet alle stetig/differenzierbar/integrierbar sind, ist es auch die Funktion ?“ Antworten bzw. hinreichende Entscheidungskriterien auf diese Fragen liefern Sätze aus der Analysis. Häufig nützt es zum Beispiel, wenn die Funktionenreihe nicht nur in jedem Punkt gegen die Grenzfunktion konvergiert, sondern im Definitionsbereich sogar gleichmäßige Konvergenz vorliegt. In einem solchen Fall ist, falls die alle stetige Funktionen waren, auch die Grenzfunktion stetig.[86] Ähnliche Voraussetzungen gelten für Beschränktheit (falls alle Partialsummen beschränkt sind),[87] Differenzierbarkeit und Integrierbarkeit der Grenzfunktion, falls alle Summanden die entsprechenden Eigenschaften haben.
Vertauschen von Reihen mit Differentialoperator und Integral
BearbeitenIm Gebiet der gleichmäßigen Konvergenz darf eine Reihe gliedweise integriert werden:
Ebenso darf sie gliedweise differenziert werden, sofern die entstehende Reihe gleichmäßig konvergiert:[88]
Da Differenzierbarkeit eine lokale Eigenschaft ist, kann dies unter Ausschöpfen offener Bereiche durch kompakte Mengen gegebenenfalls auch auf allgemeinere Funktionen ausgeweitet werden.
In einigen Anwendungen stellen die oberen Kriterien beim Vertauschen von Summe und Integral jedoch zu große Hürden dar. Zum einen decken sie nicht Maßräume unendlichen Volumens ab (wie zum Beispiel Intervalle wie oder mit dem eindimensionalen Lebesgue-Maß), zum anderen kann die Forderung nach gleichmäßiger Konvergenz große Schwierigkeiten mit sich bringen. Mit Resultaten aus der Funktionalanalysis, wie dem Satz von Fischer-Riesz, können jedoch weit allgemeinere Aussagen erzielt werden, die allerdings auch deutlich schwerer zu beweisen sind. Einer davon ist der Satz über die gliedweise Integration von Reihen: Ist ein Banachraum (zum Beispiel ) und eine Folge in (wobei ein Maß auf und eine zugehörige -Algebra des Raumes ist), und gilt
- ,
so ist -fast überall absolut konvergent und -integrierbar. Es gilt zudem[89]
Dies ist eine Folgerung aus dem Satz von der majorisierten Konvergenz. Zu beachten ist, dass dieser sehr allgemeine Satz gänzlich auf Forderungen wie gleichmäßige Konvergenz verzichtet. Unter Benutzung der -Folgenräume sowie des Zählmaßes ist ein Spezialfall, dass unter Voraussetzung von bereits Konvergenz der Doppelreihe und zudem
folgt.[90]
Es existieren jedoch auch Anwendungen, in denen weder gleichmäßige Konvergenz von noch Integrierbarkeit der oben gewählten „Majorante“ vorliegt. In solchen Fällen kann der Satz von der majorisierten Konvergenz unter Umständen dennoch einen Ausweg darstellen, wobei jedoch die Einzelfälle genauer betrachtet werden müssen. Es ist lediglich notwendig, die Partialsummen der zu integrierenden punktweise konvergenten Funktionenreihe durch eine integrierbare und von unabhängige Majorante nach oben abzuschätzen, wobei aber manchmal auf die gegebenenfalls zu grobe Dreiecksungleichung verzichtet werden kann. Ein Beispiel ist der Beweis der Leibnizreihe
durch Integrale. Jeder der Terme erfüllt
Allerdings ist die Reihe im Intervall zwar punktweise konvergent, aber weder gleichmäßig konvergent, noch ist die absolute „Majorante“ auf integrierbar, weshalb die Dreiecksungleichung nicht verwendet werden kann. Mit der feineren Abschätzung alternierender Reihen werden jedoch die Vorzeichenwechsel berücksichtigt, und es ergibt sich mit der Monotonie der Folge
für alle und . Da offenbar über absolut integrierbar ist, darf Summation und Integration vertauscht werden:
Hierbei bezeichnet den Arkustangens.
Holomorphe Grenzfunktionen
BearbeitenEs gibt auch hinreichende Kriterien für die Holomorphie der Grenzfunktion. Genauer lässt sich der Weierstraßsche Konvergenzsatz auf unendliche Reihen anwenden:[91] Ist eine Folge holomorpher Funktionen, so konvergiert gegen eine holomorphe Funktion , falls sie in normal konvergiert, d. h. für jeden Punkt gibt es eine Umgebung , sodass
Typen von Funktionenreihen
BearbeitenMan kann fragen, ob und durch welche Reihe sich eine Funktion darstellen lässt. So eine Darstellung nennt sich Reihenentwicklung. Es existieren je nach Kontext verschiedene relevante Reihenentwicklungen für gewisse Klassen von Funktionen.
Potenzreihen, Taylorreihen und analytische Funktionen
BearbeitenBei analytischen Funktionen wird eine Funktion um einen „Definitionspunkt“ herum über Polynome angenähert. Eine Möglichkeit, dies zu realisieren und zu verstehen, besteht darin, die Funktion zunächst sehr stark einzuschränken, also nur Eingabewerte aus einem sehr „kleinen“ Vorrat einzusetzen. Klein bedeutet in diesem Zusammenhang, dass die betrachteten Eingabewerte sehr nahe beieinander liegen. Soll eine Funktion etwa um 0 herum studiert werden, würden Werte wie 0,000001 vielleicht noch in Betracht gezogen, möglicherweise aber nicht mehr 1, geschweige denn 100. In diesem Zusammenhang nennt man die 0 auch den Entwicklungspunkt. Hinter diesem Prinzip steckt eine gewisse Form der „Stetigkeit“: Wurde eine analytische Funktion im Punkt 0 gut verstanden, so lässt sich daraus schon auf ihr Verhalten in zum Beispiel 0,000001 schließen, und das nur anhand der vier Grundrechenarten. Präziser wird die Annäherung über Polynome realisiert, also Ausdrücke wie , und ganz allgemein
Eine analytische Funktion kann also um jeden Wert ihres Definitionsbereichs durch Anwendung der Grundrechenarten entwickelt werden. Dabei ist zu beachten, dass es sich bei hinreichend „komplizierten“ Funktionen nur um eine Näherung handelt. Eine zentrale Eigenschaft der Analytizität ist aber, dass für solche komplizierten Funktionen beliebig lange Polynomketten, also addierte -Terme, zur Annäherung gefunden werden können. Je länger diese Terme sind, desto besser. Lässt man diesen Prozess gegen Unendlich streben, ist die Annäherung in den umliegenden Punkten perfekt, es herrscht also Gleichheit. In diesem Sinne sind also analytische Funktionen, zumindest lokal, gerade „unendlich lange Polynome“. Diese werden auch als Potenzreihen bezeichnet. Obwohl dabei unendlich viele Terme addiert werden, kann Konvergenz vorliegen, wenn das Funktionsargument nahe genug am Entwicklungspunkt liegt. Wählt man zum Beispiel den Entwicklungspunkt 0 und für die Koeffizienten die Dezimalstellen der Kreiszahl , also
so gilt
Für Werte wird dann „erst recht“ endlich sein. Diesem Gedanken folgend kann man etwa über das Majorantenkriterium (siehe unten) zeigen, dass Potenzreihen entweder überall oder innerhalb von Intervallen (für komplexe Zahlen Kreisscheiben) mit dem Entwicklungspunkt als Zentrum konvergieren.

Beispiel: Eine in der Schule behandelte Funktion, die sich im Allgemeinen nicht durch nur endlichfache Anwendung der vier Grundrechenarten berechnen lässt, ist der Sinus, also die Vorschrift . Hier wird die Vorschrift zunächst nicht über eine Zahlenrechnung, sondern geometrisch erklärt. Zur Länge eines Kreisbogens soll die zugehörige gerade Strecke gefunden werden, die den Endpunkt des Bogens mit der Grundachse verbindet, analog beim Kosinus (siehe Bild). Alle betrachteten Strecken haben Längen, im Verhältnis zur Einheit dimensionslos, also entspricht dies einer Abbildung von Zahlen auf Zahlen. Krumme Kreislinien („komplizierte Strecken“) werden auf ungleich lange gerade Linien („einfache Strecken“) abgebildet, was vermuten lässt, dass sich diese Umrechnung nicht in einfacher Weise mit den vier Grundrechenarten darstellen lässt. Es zeigt sich jedoch, dass der Sinus eine analytische Funktion ist, weshalb eine Annäherung durch einfache Terme möglich ist. Es gilt zum Beispiel für sehr kleine Werte von
Dies entspricht einem „Studium“ der Sinusfunktion in oben erklärtem Sinne, da die „komplizierte Sinusfunktion“ durch eine einfache Abbildung angenähert wurde. Dabei war der Entwicklungspunkt 0, in der Tat ist wegen die Annäherung hier perfekt, doch auch für umliegende Werte ist sie brauchbar. Es gilt zum Beispiel
- und .
Zur exakten Berechnung erhält man für den Sinus[92]
wobei die Fakultät bezeichnet. Die Formel erweitert sich auch auf alle komplexen Zahlen und setzt den Sinus dort als holomorphe Funktion fort, wobei dort keine geometrische Interpretation über Dreiecke mehr zur Verfügung steht, aber im Gegenzug die enge Verbindung zur komplexen Exponentialfunktion deutlicher wird.
Über das Beispiel des Sinus erklärt sich auch das allgemeine Verfahren zum Aufstellen einer Taylorreihe zu einer analytischen Funktion . Wird als Entwicklungspunkt gewählt, so gilt die Formel
- mit -te Ableitung von an der Stelle ,
für alle , die nahe genug an liegen. Dabei bezeichnet die -te Ableitung von an der Stelle . Genau genommen muss gelten, wobei die Zahl den Konvergenzradius der Taylorreihe bezeichnet.[93] Ist der Entwicklungspunkt , spricht man gelegentlich auch von einer Maclaurinschen Reihe.[94] Sind auch negative ganzzahlige Exponenten von vorhanden, verallgemeinert sich das Konzept zu Laurent-Reihen.
| Beispiel: Approximation der Zahl |
|
Taylorentwicklungen lassen sich zum Beispiel an der Wurzelfunktion demonstrieren, etwa um den Punkt . Diese ist dort analytisch, man hat die Ableitungen und . Also gilt mit der Taylor-Formel die Approximation für Zahlen , die nahe an liegen. Der Ausdruck auf der rechten Seite kann, wie oben, durch Anwendung nur der vier Grundrechenarten schnell berechnet werden. Er stimmt nach Einsetzen von exakt mit dem Funktionswert überein, doch auch in der näheren Umgebung von ist die Annäherung noch sehr genau. Man hat etwa und es gilt für den exakten Wert . |
Die Theorie der analytischen Funktionen wird erst über den komplexen Zahlen vollständig erfassbar. Hier spricht man synonym von holomorphen Funktionen und es gilt der Cauchysche Entwicklungssatz: Ist mit offenem , die größte Kreisscheibe um in und holomorph, so ist um in eine Taylorreihe entwickelbar, die in auf kompakten Teilmengen absolut und gleichmäßig konvergiert. Die Koeffizienten sind gegeben durch[95]
- , wobei
Dabei wird der Integrationsweg in mathematisch positiver Richtung einfach durchlaufen. Bemerkenswert ist die Tatsache, dass für den Beweis des Entwicklungssatzes lediglich die Reihenentwicklungen der Funktionen benötigt werden (siehe auch geometrische Reihe) sowie Vertauschbarkeit von Summation und Integration. Für den Fall wurde dies bereits 1831 von Cauchy durchgeführt.[96]
Da jede holomorphe Funktion analytisch ist und umgekehrt, lassen sich Eigenschaften von Potenzreihen direkt auf holomorphe Funktionen übertragen. Dies stellt gleichzeitig den Weierstraßschen Zugang zur Funktionentheorie dar, der die Darstellbarkeit von Funktionen als Potenzreihen zum Ausgangspunkt hat.[53]
Potenzreihen können auch als sog. Lambertreihen geschrieben werden.
Fourierreihen
BearbeitenAls Fourierreihe einer Funktion bezeichnet man ihre Entwicklung nach trigonometrischen Funktionen. Dies betrifft vornehmlich periodische Funktionen, also Funktionen, die sich intervallweise immer wieder in ihrem Abbildungsverhalten wiederholen. Da eine Normierung der Periode durch entsprechende Skalierung im Funktionsargument erreicht werden kann, genügt es, sich -periodische Funktionen anzuschauen, also solche mit der Eigenschaft .
Fourierreihen spielen eine Rolle bei der Überlagerung von Wellen, zum Beispiel bei der Erzeugung von Klängen. Erklingen mehrere Töne gleichzeitig, etwa bei einem Musikstück, so entspricht dies physikalisch einer Überlagerung verschiedener Schallwellen. Um die Gesamtsituation zu erfassen, ist die Addition der entsprechenden (nach Phase und Amplitude skalierten) Sinuskurven erforderlich. Gewisse periodische Signale, zum Beispiel in der Elektrotechnik, haben jedoch ein derart komplexes Muster, dass eine unendliche Anzahl verschiedener Sinuswellen benötigt wird, um sie exakt darzustellen.

Ist eine -periodische Funktion, etwa ein Signal, gegeben, so ist eine Entwicklung in eine Fourierreihe (zumindest formal) dann möglich, wenn auf dem Interval integrierbar ist. In diesem Fall macht es Sinn, den -ten Fourierkoeffizienten über die Formel
zu definieren. Es ist dabei die Eulersche Identität zu beachten, die den entscheidenden Zusammenhang zwischen der komplexen Exponentialfunktion und den trigonometrischen Funktionen herstellt. Da -periodisch ist, sollten diese Integrale „alle Daten“ von beinhalten. Die Aussage ist nun, dass die Kollektion der Koeffizienten mit unter Umständen ausreicht, das gesamte Signal vollständig zu rekonstruieren. Dies wird über die Konvergenz der zunächst nur formalen Fourierreihe
realisiert.[97] Ist zum Beispiel stetig differenzierbar, so wird die zugehörige Fourierreihe gleichmäßig gegen konvergieren. Allgemein bezeichnet man Kriterien, die Konvergenz(arten) von Fourierreihen festlegen, auch als Dirichlet-Bedingungen. Zum Beispiel verrät das Verhalten der Funktion einiges über die Fourierkoeffizienten: Wenn eine 1-periodische Funktion mit ihren Ableitungen bis zur -ten Ordnung stetig ist, dann streben für die Terme gegen Null.[98] Ist umgekehrt stetig und konvergiert , so ist bereits stetig differenzierbar und es gilt .[99]
Es kann die Fourierreihe zu auch ausschließlich in Termen von Sinus und Kosinus ohne komplexe Zahlen statt der Exponentialfunktion ausgedrückt werden, wobei die Wellenüberlagerung ersichtlicher wird. Allerdings ist die Nutzung komplexer Zahlen in der Elektrotechnik, auch im Kontext von Wellen, durchaus üblich.[100]
Fourierreihen können auch im Komplexen betrachtet werden. Ist auf dem offenen Streifen
holomorph und -periodisch, gilt also stets , so besitzt eine Fourier-Entwicklung
Dies ist auf ganz absolut und lokal gleichmäßig konvergent. Eine Berechnung der Koeffizienten ist für jedes durch
möglich.[101] Entscheidend für die Herleitung der Existenz einer Fourierreihe auf horizontalen Streifen ist das Abbildungsverhalten der komplexen Exponentialfunktion sowie die Existenz der Laurent-Reihe.[102] Die Entwicklung holomorpher Funktionen in Fourierreihen spielt zum Beispiel eine große Rolle in der Theorie der Modulformen.[103]
Dirichletreihen
BearbeitenDirichletreihen kommen vor allen Dingen in der Zahlentheorie zum Einsatz. Damit ist die Teildisziplin der Mathematik gemeint, die sich mit den Eigenschaften ganzer und auch rationaler Zahlen befasst. Viele Fragestellungen, etwa aus der multiplikativen Zahlentheorie, hängen dabei mit Primfaktorzerlegungen zusammen. An diesem Punkt kommen Dirichletreihen ins Spiel. Diese ahmen in manchen Fällen Primfaktorzerlegungen nach und übertragen dieses zahlentheoretische Element damit direkt in die Funktionentheorie.
Als Dirichletreihe bezeichnet man eine Entwicklung
- mit
In gewisser Weise handelt es sich um eine „Potenzreihe unter Vertauschung der Rollen“: Bei Dirichletreihen wird über die Basis der Potenz summiert und nicht über den Exponenten, wie es bei in Potenzreihen noch der Fall war. Während Potenzreihen im Komplexen auf Kreisscheiben konvergieren, konvergieren Dirichletreihen im Komplexen auf rechten Halbebenen. Ist eine Dirichletreihe zudem in einem Punkt konvergent, so ist sie in jedem Punkt mit absolut konvergent. Der Bereich der absoluten Konvergenz ist wieder eine Halbebene, die von der Halbebene der Konvergenz umschlossen wird.
Die sich aus den Potenzgesetzen ergebende Rechenregel macht Dirichletreihen für die Zahlentheorie interessant. Sind nämlich die Koeffizienten ebenfalls (stark) multiplikativ, gilt also so existiert im Bereich der absoluten Konvergenz das Euler-Produkt
Kann die Funktion , ähnlich wie ein Polynom, auch über ihre Nullstellen in ein Produkt faktorisiert werden, können damit Verbindungen zwischen Primzahlen und Eigenschaften von Nullstellen spezieller Funktionen aufgebaut werden. Dies betrifft zum Beispiel die Riemannsche Zeta-Funktion
deren Nullstellen in Dualität zur Folge der Primzahlen steht.[104] Die Lage der Nullstellen in der komplexen Ebene ist Gegenstand der Riemannschen Vermutung. Eine ähnlich tiefe Vermutung, die Vermutung von Birch und Swinnerton-Dyer, befasst sich ebenfalls mit Nullstellen von Dirichletreihen, die ein Euler-Produkt besitzen. Eine sehr weitreichende Verallgemeinerung findet die Riemannsche Zeta-Funktion in den L-Funktionen.
Partialbruchzerlegungen und elliptische Funktionen
BearbeitenIn der komplexen Ebene können manche Funktionen durch „Interpolation ihrer Singularitäten“ generiert werden. Dies trifft auf rationale Funktionen zu, kann aber in einigen Fällen durch unendliche Reihen ausgedehnt werden. Ist eine ganze Funktion, die für Konstanten stets die Ungleichung
erfüllt, so gilt bereits[105]
Ist zusätzlich eine ungerade Funktion, ist also stets , gilt
Für führt dies, nach einem Shift im Argument, zur Partialbruchzerlegung des Kotangens:
Dieses Konzept lässt sich auf Gitter ausweiten. Seien zwei komplexe Zahlen, die über linear unabhängig sind und sei das Gitter, das von und erzeugt wird. Dann ist die Weierstraßsche -Funktion zum Gitter wie folgt definiert:[106]
Die Reihe konvergiert lokal gleichmäßig absolut in . Es handelt sich um eine doppelperiodische, also elliptische Funktion.[107] Eng verwandt zu den elliptischen Funktionen sind die sog. Eisensteinreihen.[108]
Konvergenzkriterien
BearbeitenZwar gibt es kein brauchbares, allgemeingültiges Kriterium, um zu entscheiden, ob eine Reihe konvergiert,[109] aber in manchen Spezialfällen lassen sich unter zusätzlichen Annahmen Kriterien angeben, die auf ganz unterschiedlichen mathematischen Techniken basieren.
Allgemeine Kriterien
BearbeitenNullfolgenkriterium
BearbeitenWenn die Reihe konvergiert, dann konvergiert die Folge der Summanden für gegen 0. Kontraponiert: Ist keine Nullfolge, so divergiert die entsprechende Reihe.[13]
Zudem gilt der Satz von Olivier: Ist monoton fallend und konvergent, so folgt bereits .[110]
| Beispiel |
|
Es kann die Reihe (trotz beschränkter Partialsummen) nicht konvergieren, da nicht gegen 0 konvergiert. |
Die Umkehrung ist nicht allgemeingültig (ein Gegenbeispiel ist die harmonische Reihe). Das Nullfolgenkriterium wird daher in erster Linie zum Nachweis der Divergenz einer Reihe verwendet.
Teleskopreihen
BearbeitenDie Teleskopreihe konvergiert genau dann, wenn die Folge gegen eine Zahl konvergiert. Der Wert der Reihe ist dann .
| Beispiel |
|
Es gilt , da gegen konvergiert, und . |
Majorantenkriterium
BearbeitenWenn alle Glieder der Reihe nichtnegative reelle Zahlen sind, konvergiert und für alle zudem gilt, dann konvergiert auch die Reihe absolut, und es ist[111]
- .
| Beispiel |
|
Es konvergiert für alle die Reihe . In der Tat, da , folgt über die Behauptung mit dem Majorantenkriterium. |
Minorantenkriterium
BearbeitenWenn alle Glieder der Reihe nichtnegative reelle Zahlen sind, divergiert und für alle zudem mit nichtnegativen reellen Zahlen gilt, dann divergiert auch die Reihe .
| Beispiel |
|
Es gilt für alle . Da nun folgt die Divergenz der Reihe mit dem Minorantenkriterium. |
Quotientenkriterium
BearbeitenEs wird die Reihe mit für alle bis auf endlich viele betrachtet (alternativ kann im Voraus die Folge auch unter Weglassen der Nullen auf eine Teilfolge verdichtet werden, die ohne Einschränkung wieder als bezeichnet werden kann). Dann gilt:[112]
- Falls , so ist die Reihe absolut konvergent (dabei steht für den Limes superior).
- Falls , so ist die Reihe divergent (dabei steht für den Limes inferior).
- In den verbleibenden Fällen kann keine Aussage getroffen werden, d. h., sowohl bedingte oder absolute Konvergenz, aber auch Divergenz sind möglich.
Die Berechnung der obigen Limites superior und inferior kann schwierig sein, weshalb in vielen Fällen lediglich eine Abschätzung gemacht wird. Ist zum Beispiel für alle bis auf endlich viele für eine feste Zahl , so gilt insbesondere , also ist die Reihe absolut konvergent.
Wurzelkriterium
BearbeitenZu einer Reihe wird die Größe betrachtet (dabei steht für den Limes superior). Dann gelten folgende Aussagen:[113]
- Ist , so konvergiert die Reihe absolut.
- Ist , so ist die Reihe divergent.
- Ist , so kann keine Aussage getroffen werden, d. h., sowohl bedingte oder absolute Konvergenz, aber auch Divergenz sind möglich.
Im Falle von Potenzreihen dient das Wurzelkriterium beim Beweis der Formel von Cauchy-Hadamard für deren Konvergenzradius.[114]
Die Berechnung der obigen Limites superior und inferior kann schwierig sein, weshalb in vielen Fällen lediglich eine Abschätzung gemacht wird. Ist zum Beispiel für alle bis auf endlich viele für eine feste Zahl , so gilt insbesondere , also ist die Reihe absolut konvergent.
Kriterium von du Bois-Reymond und Dedekind
BearbeitenDieses Kriterium kann in zwei Unterkriterien unterteilt werden.
- Es ist die Reihe konvergent, falls absolut und wenigstens bedingt konvergiert.
- Es ist die Reihe konvergent, falls außer der absoluten Konvergenz von lediglich die Beschränktheit der Partialsummen von und vorausgesetzt wird.[115]
Gaußsches und Weierstraßsches Kriterium
BearbeitenKann man den Quotienten in der Form mit einer beschränkten Folge und schreiben, so ist die Reihe im Falle konvergent, und im Falle divergent.[116]
Dieses Kriterium von Gauß kann für komplexe Folgen ausgeweitet werden, wo es als Kriterium von Weierstraß benannt ist. Erfüllen die komplexen Glieder
mit und beschränkten , so konvergiert die zugehörige Reihe genau dann absolut, wenn . Ist , so sind wenigstens die Reihen und konvergent.[117]
Kriterien unter Monotoniebedingungen
BearbeitenMonotoniekriterium
BearbeitenGilt für alle , so konvergiert genau dann, wenn die Folge beschränkt ist, und der Grenzwert ist .[118] Ist in diesem Szenario zusätzlich monoton fallend, impliziert die Konvergenz der Reihe auch .[119]
Es ist für beliebige positive die Reihe
konvergent.[120]
Integralkriterium
BearbeitenIst eine monoton fallende Funktion mit
- für alle ,
dann konvergiert genau dann, wenn das uneigentliche Integral
| Beispiel |
|
Die Dirichletreihe konvergiert für und divergiert für , was mit dem Integralkriterium gezeigt werden kann. Als Funktion von aufgefasst, ergibt diese Reihe die Riemannsche Zeta-Funktion. |
Leibniz-Kriterium
BearbeitenEine Reihe der Form
mit nichtnegativen wird alternierende Reihe genannt. Eine solche Reihe konvergiert, wenn die Folge monoton gegen 0 konvergiert.[122] Die Umkehrung ist nicht allgemeingültig.
Kriterium von Abel
BearbeitenEs ist die Reihe konvergent, falls die Reihe konvergiert, und die Folge monoton und beschränkt ist.[115]
Kriterium von Dirichlet
BearbeitenEs ist die Reihe konvergent, falls
also die Partialsummen der beschränkt sind, und wenn eine monoton fallende Nullfolge ist.[115] Dabei steht für das Supremum.
Cauchysches Verdichtungskriterium
BearbeitenIst eine monoton fallende Nullfolge, so konvergiert die Reihe genau dann, wenn die Reihe konvergiert.[123]
Multiplikative Funktionen
BearbeitenEs ist eine multiplikative Funktion, falls für alle teilerfremden und gilt.
Es konnte Peter D. T. A. Elliott Folgendes zeigen: Es sei multiplikativ, sodass
existiert, und ferner
Dann gilt bereits, dass die Reihen
sämtlich konvergieren.[124]
Funktionentheoretische Mittel
BearbeitenSätze von Tauber und Littlewood
BearbeitenDer Satz von Tauber, bewiesen von Alfred Tauber im Jahr 1897,[125] nutzt das Randverhalten einer Potenzreihe, um ein hinreichendes Kriterium für dortige Konvergenz zu geben. Ist
für alle konvergent, existiert und gilt für , so konvergiert gegen . John Edensor Littlewood konnte dieses Resultat verbessern, indem er zeigte, dass bereits die abgeschwächte Bedingung für alle mit einer Konstante für die Aussage des Satzes hinreichend ist.[126] Diese Bedingung kann im allgemeinen Fall nicht weiter verbessert werden: Zu jeder positiven, wachsenden Funktion mit existiert eine Abel-summierbare Folge mit , sodass divergiert.[127] Wird allerdings gefordert, dass die fast alle nichtnegativ sind, kann die Bedingung der Beschränktheit von gänzlich weggelassen werden.[128]
genau dann, wenn .[129]
Ist stets für eine reelle Zahl , dann folgt aus bereits .[130]
Kriterien von Fatou und Korevaar
BearbeitenWieder habe einen Konvergenzradius von mindestens 1. Gibt es sogar eine Konstante , sodass mit , so folgt bereits[131]
Ist um holomorph fortsetzbar und gibt es eine nicht-fallende Funktion , sodass für und für mit einer Konstanten ; gilt zudem für alle , dann konvergiert gegen und zudem gilt[132]
Eine ähnliche Aussage gilt für Dirichlet-Reihen: Ist eine Funktion, die für alle konvergiert und sich nach holomorph fortsetzen lässt; gilt ferner für ein wie oben, so gilt bereits[133]
Abel-Summierbarkeit
BearbeitenMan nennt eine formale Reihe Abel-summierbar gegen , falls[134]
wobei die Reihe zur Linken für alle konvergiere. Es ist eine Abel-summierbare Reihe genau dann konvergent, wenn[135]
Satz von Fatou
BearbeitenDer Satz Fatou besagt, dass, wenn die Potenzreihe
für alle konvergiert, und sich die Funktion in einer Umgebung des Randpunkts holomorph fortsetzen lässt, aus bereits folgt, dass konvergiert, und den Wert annimmt.[136]
Der Satz von Fatou kann, unter Umgehung der Bedingung der Holomorphie in , ausgeweitet werden. Dafür wird das Konzept des Hardy-Raums eines Gebietes benötigt. Erfüllt im Randpunkt die lokale -Bedingung, so existiert eine Zahl , sodass für in gegen eine (integrierbare) Funktion konvergiert (siehe auch Lp-Raum), also
Ist die Menge der Randpunkte , mit , an der singulär ist in dem Sinne, dass sie dort nicht die lokale -Bedingung erfüllt, eine Nullmenge, und gilt
dann konvergiert in jedem Punkt gegen , an dem der Differenzenquotient
die lokale -Bedingung in erfüllt.[137] Dabei steht für das Supremum.
Satz von Ingham
BearbeitenEin im Jahr 1935 gegebener Satz von Albert Ingham war Ausgangspunkt für weitere Untersuchungen von Donald Newman, der diesen mit einfachen funktionentheoretischen Mitteln beweisen konnte. Sei eine Dirichletreihe
für alle mit konvergent (d. h., sie stellt in dieser offenen Halbebene eine holomorphe Funktion dar). Lässt sich nun holomorph auf eine offene Menge fortsetzen, die vollständig enthält, und sind die beschränkt, so gilt bereits für alle [138]
Für unbeschränkte ist die obige Aussage bekanntlich falsch.
Methoden zur Grenzwertbestimmung
BearbeitenEs existiert kein allgemein brauchbares Verfahren, den Grenzwert einer konvergenten Reihe explizit auszurechnen. In einigen Fällen lassen sich Grenzwerte auch nicht auf „elementare“ mathematische Konstanten zurückführen, etwa im Fall der Apéry-Konstante
Allerdings gibt es einige Techniken, die in speziellen Situationen die geschlossene Berechnung eines konvergenten Reihenausdrucks ermöglichen.
Teleskopreihen
BearbeitenHat eine Reihe die Gestalt mit einer Folge , die gegen einen Grenzwert konvergiert, so konvergiert jene ebenfalls und hat den Grenzwert .[139] Dieses Resultat lässt sich weiter verallgemeinern. Sind die Glieder der Reihe gegeben durch
- mit ,
wobei gegen den Grenzwert konvergiert und , so konvergiert und der Grenzwert ist explizit gegeben durch[140]
- .
Ein Anwendungsbeispiel dieser Regel ist[141]
Abelscher Grenzwertsatz
BearbeitenEs sei eine konvergente Reihe. Eine Möglichkeit, ihren Grenzwert zu bestimmen, geht über die von den erzeugte Funktion. Niels Henrik Abel konnte beweisen, dass sich die Funktion
stetig nach fortsetzen lässt. Ferner gilt

Mit diesem Ansatz können manche klassischen Reihengrenzwerte berechnet werden.[142] Beispielsweise gilt für alle mit gilt die Reihendarstellung
Mit dem Leibniz-Kriterium und der Abel-Summierbarkeit folgt damit die Leibniz-Reihe:[143]
Ähnlich verhält es sich mit der Taylorreihe des natürlichen Logarithmus:
Damit folgt, dass die alternierende harmonische Reihe den Grenzwert besitzt:[144]
Beide Reihen zeigen zwar ein klares „Bildungsgesetz“, sind jedoch für numerische Berechnungen unbrauchbar.[145]
Differential- und Integralrechnung
BearbeitenAnsätze über Differential- und Integralrechnung greifen primär auf Eigenschaften von Potenzreihen zurück. In manchen Fällen kann der Grenzwert einer Reihe ermittelt werden, indem man die allgemeinere Potenzreihe für Werte studiert. Im einfachsten Fall gilt:
- Die Reihe hat Konvergenzradius ,
- und es lässt sich durch bekannte Funktionen geschlossen ausdrücken.
Dann kann mit
direkt ein geschlossener Grenzwert hingeschrieben werden, und Konvergenz folgt ebenso automatisch. Ist der Konvergenzradius jedoch genau , muss im Rahmen des Abelschen Grenzwertsatzes zunächst Konvergenz nachgewiesen werden (siehe oben).
Dieser Ansatz kann schnell auf Reihen des Typs
mit verallgemeinert werden. In der obigen Situation mit Konvergenzradius sind diese sämtlich absolut konvergent, und Grenzwerte können geschlossen über die höheren Ableitungen der Funktion an der Stelle ausgedrückt werden. Zum Beispiel gilt mit obiger Notation
und ganz allgemein
- (für ),
wobei die Stirling-Zahlen zweiter Art sind.[146] Ein einfaches Beispiel betrifft die Reihe
Es gilt mit der geometrischen Reihe für alle (weshalb die betrachtete Reihe definitiv absolut konvergiert), und mit der Grenzwert .
Mitunter noch einfacher gestaltet sich dieser Ansatz beim Übergang zu Fourierreihen durch den Variablenwechsel . Man betrachtet dann
im Punkt und beim Ableiten dieser Reihe sind keine Stirling-Zahlen mehr vonnöten (allerdings wird gleichzeitig wegen Verkettung das Aufstellen geschlossener Ableitungsterme meist schwieriger). Im Rahmen der charakteristischen Funktion ist dieses Vorgehen in der Wahrscheinlichkeitstheorie bei der Berechnung von Momenten diskreter Zufallsvariablen nützlich, siehe auch momenterzeugende Funktion.
In einigen Fällen können Reihen direkt auf gewisse Integrale zurückgeführt werden, wobei Letztere dann mit Methoden der Analysis, zum Beispiel durch Auswertung mit Angabe einer Stammfunktion, gelegentlich geschlossen berechnet werden können. Die Umwandlung von Integral in Reihe ergibt sich dabei im Falle von Funktionenreihen oft durch gliedweise Integration. Ein Beispiel ist die Leibniz-Reihe:[147]
David Bailey, Peter Borwein und Simon Plouffe benutzten die Integralformel
beim Beweis der Bailey-Borwein-Plouffe-Formel für die Kreiszahl .[148] Ein anderes Beispiel betrifft eine Lösung des Basler Problems über den Ansatz
- ,
wobei den Areatangens Hyperbolicus bezeichnet.[149]
Fourieranalysis
BearbeitenDie Grenzwertbestimmung über Fourierreihen ähnelt dem Grenzwertsatz von Abel insofern, als dass die Reihe auch hier als Wert einer zu bestimmenden Funktion interpretiert wird. Weiß man, dass absolut konvergiert, so kann man diesen Wert als mit
auffassen. Dann ist eine 1-periodische Funktion und die rechte Seite ihre Darstellung als Fourierreihe. Über die Umrechnungsformel
können die Koeffizienten der Reihe aus zurückgewonnen werden. Es muss also ein „passendes“ zu den gefunden werden. Zum Beispiel findet man mit partieller Integration schnell
womit durch Einsetzen von die Antwort auf das Basler Problem folgt.[150] Ist lediglich als auf dem Intervall integrierbar vorausgesetzt, und hat die assoziierte Fourierreihe , so gilt außerdem die Parsevalsche Identität[151]
Residuensatz
BearbeitenIn manchen Fällen, besonders bei unendlichen Reihen über rationale Funktionen, kann der Residuensatz aus der Funktionentheorie verwendet werden. Ist eine meromorphe Funktion mit endlichen vielen, nicht ganzzahligen Polstellen , so gilt, falls zusätzlich mit und , die Formel
Ähnlich gilt[152]
Dabei bezeichnet den Kotangens und den Kosekans. Diese Aussage beinhaltet folgenden Spezialfall: Sind und Polynome, sodass und für alle , so folgt
Mit diesem Verfahren lässt sich zum Beispiel und zeigen.
Ist eine ganze Funktion, sodass es eine Folge gibt, sodass
- ,
dann gilt[153]
Wird durch ersetzt, gilt unter sonst gleichen Bedingungen[154]
Ungleichungen
BearbeitenUngleichungen für Reihen verwenden oft spezielle analytische Methoden, etwa aus der Fourier-Analysis.
Dreiecksungleichungen
BearbeitenEs gilt stets für reelle oder auch komplexe
Dies ist die Dreiecksungleichung für Reihen.[155] Sind die Zahlen reell, gilt Gleichheit genau dann, wenn sämtliche nicht-negativ oder nicht-positiv sind. Für allgemeine komplexe Zahlen gilt Gleichheit genau dann, wenn alle auf einer gleichen, bei startenden, Halbgeraden in der komplexen Ebene liegen (mit anderen Worten, dass alle dasselbe komplexe Argument haben). Dies ergibt sich mit aus der umgekehrten Dreiecksungleichung, siehe unten.
Allgemeiner gilt für Multireihen
Im Laufe der Zeit wurden zahlreiche Varianten solcher „Dreiecksungleichungen“ gefunden. Sind zum Beispiel positive Zahlen mit , so gilt stets[156]
Allgemeiner gilt für irgendwelche positiven Zahlen und sogar stets[157]
Auch umgekehrte Dreiecksungleichungen wurden gefunden. Ist und eine reelle Zahl, sodass für komplexen Zahlen stets ein und existiert mit , so gilt[158]
Diese Ungleichung verallgemeinert das Kriterium absoluter Konvergenz auf komplexe Zahlen: Liegen alle Summanden einer Reihe in einem gemeinsamen Winkelbereich, dessen Aufspannung weniger als (also 180 Grad) entspricht, konvergiert genau dann absolut, wenn die Folge der Absolutwerte der Partialsummen beschränkt ist. Zu beachten ist jedoch, dass dieses Kriterium und auch eine Ungleichung oberen Typs für den Fall reeller mit gemischten Vorzeichen im Allgemeinen nicht existiert, da , weshalb hier je nach Einzelfall andere Methoden zur Abschätzung gefunden werden müssen. Aus unter anderem diesem Grund sind Reihen mit reellen Gliedern gemischten Vorzeichens nicht nur besonders interessant, sondern gleichzeitig auch besonders schwierig.
Sind allgemein komplexe Zahlen, so existiert stets eine (von diesen Zahlen abhängige) Teilmenge , sodass[159]
Dabei bezeichnet die Kreiszahl.
Vergleich zum geometrischen Mittel
BearbeitenFür nicht-negative Zahlen gilt
Diese Ungleichung ist scharf in dem Sinne, dass Gleichheit genau dann gilt, falls . In allen anderen Fällen ist die linke Seite echt kleiner als die rechte.[160] Diese Ungleichung vergleicht arithmetisches und geometrisches Mittel.
Integralvergleich
BearbeitenIst monoton fallend, so gilt[161]
Daraus folgt direkt das Integralkriterium, also dass unter obigen Voraussetzungen die Reihe genau dann konvergiert, falls existiert.[162]
Fehler- und Restgliedabschätzung
BearbeitenAlternierende Reihen
BearbeitenIst eine monoton fallende Nullfolge, so konvergiert nach dem Leibnizkriterium gegen einen Grenzwert und es gilt[163]
Ferner gilt stets .[164] Dies kann weitreichend verallgemeinert werden: Es gilt unter oberen Voraussetzungen
für alle .[165]
Abelsche Ungleichung
BearbeitenSei eine monoton fallende Nullfolge und eine Folge mit beschränkten Partialsummen, also
Dann konvergiert und es gilt für alle die Ungleichung[166][167]
- .
Taylorreihen
BearbeitenEs können auch Restglieder in Taylorreihen abgeschätzt werden. Ist innerhalb einer offenen Menge der komplexen Zahlen, die die Kreisscheibe enthält, holomorph bzw. analytisch, so gilt für alle [168]
Damit folgt für die Restgliedabschätzung
- .
Ist insbesondere hinreichend klein, etwa , so kann dies vereinfacht durch[168]
ausgedrückt werden, wobei die implizite Konstante von und , aber nicht von und abhängt.
Symmetrische Ungleichungen
BearbeitenEine Funktion auf einem Intervall gehört der Klasse an, falls für alle sowie die Ungleichung
erfüllt ist. Unter diesen Voraussetzungen gilt für , , und beliebige positive die Ungleichung[169]
Eine direkte Folgerung ist im Falle von sowie :[170]
Besselsche Ungleichung und die Halasz-Montgomery-Ungleichungen
BearbeitenEs sei ein -Vektorraum mit Skalarprodukt . Ist ein orthonormales System von Vektoren aus , so gilt
Dies ist die sog. Besselsche Ungleichung.[171] Diese lässt sich auf die Halasz-Montgomery-Ungleichungen verallgemeinern. Sind dieses Mal irgendwelche Elemente aus , so gelten[172]
Hausdorff-Young-Ungleichung
BearbeitenSei 1-periodisch, auf integrierbar mit assoziierter Fourierreihe . Sind und so gewählt, dass , so gilt die Hausdorff-Young-Ungleichung[173]
und ihre „Duale“
- .
Cauchy-Schwarzsche Ungleichung und Höldersche Ungleichung
BearbeitenFür beliebige komplexe Zahlen gilt die folgende Ungleichung für Partialsummen[174]
Diese wird als Cauchy-Schwarzsche Ungleichung bezeichnet. Konvergieren beide Reihen für zur Rechten, kann auch auf die Konvergenz der linken Seite geschlossen werden, und es gilt die entsprechende Ungleichung für die Grenzwerte.[175][176][177] Eine unter Zusatzbedingungen verbesserte Version stammt von Nicolaas Govert de Bruijn:[178] Sind reell und komplex, dann gilt
- .
Hat man allgemein mit , so gilt allgemeiner die Höldersche Ungleichung
Es kann aus der Konvergenz des rechten Ausdrucks auf die Konvergenz der linken Reihe rückgeschlossen werden.[179] Im Grenzfall entspricht dies
- .
Die Hölder-Ungleichung lässt sich gewichten. Für positive gilt[180]
Minkowski-Ungleichung
BearbeitenWenn ist und und beliebige komplexe Zahlen sind, so gilt bereits die Minkowski-Ungleichung[181]
Die Minkowski-Ungleichung lässt sich verallgemeinern: Ist stetig, streng monoton steigend und konvex mit sowie konvex für alle , so gilt für alle nicht-negativen und
Dabei ist die Umkehrfunktion von .[182]
Gutzmersche Ungleichung
BearbeitenIst eine in einer Umgebung von holomorphe Funktion mit Potenzreihe mit dem Konvergenzradius , dann gilt für jedes mit die Ungleichung
Die Ungleichung geht auf August Gutzmer aus dem Jahr 1888 zurück.[183]
Hilbert-Ungleichung
BearbeitenIst auf der abgeschlossenen Einheitskreisscheibe holomorph, so gilt bereits die Hilbert-Ungleichung[184]
Der Faktor ist dabei optimal.[185] Dies kann auf allgemeinere diskrete Mengen ausgeweitet werden. Sind und
dann gelten[186]
Eine weitere Variante der Hilbert-Ungleichung betrifft stetige Funktionen . Es gilt[187]
Eine andere Variante betrifft bestimmte Exponentialreihen. Für komplexe und reelle Zahlen mit für alle gilt[188]
Van der Corputsche Ungleichung
BearbeitenDiese ist eine Anwendung der Cauchy-Schwarzschen Ungleichung. Für komplexe Zahlen sowie natürliche Zahlen gilt[189][190]
Dabei bezeichnet die komplexe Konjugation der Zahl .
Diese Aussage kann weiter verallgemeinert werden. Sei ein Fourier-Polynom
mit und für alle . Dann gilt[191]
Exponentialsummen
BearbeitenKusmin-Landau-Ungleichung
BearbeitenEs sei , sodass monoton für für gewählte ganzzahlige . Es gebe nun und sodass
für alle . Dann gilt[192]
In einer Variante bleibt die Gültigkeit dieser Ungleichung bestehen, wenn stetig differenzierbar ist mit monotoner Ableitungsfunktion , sodass .[193]
Der Satz von van der Corput
BearbeitenSei , und seien ganze mit gewählt. Es sei stets positiv oder stets negativ. Ist , so ist[194]
Ist überdies mit einem , so gilt
Sowohl die Kusmin-Landau-Ungleichung als auch der Satz von van der Corput besitzen höherdimensionale Verallgemeinerungen.[195]
Weyl-Ungleichung
BearbeitenIst ein reelles Polynom mit Grad , dessen Leitkoeffizient eine Approximation
mit und sowie einem fixierten hat, so gibt es für jedes eine Konstante mit[196]
Das große Sieb
BearbeitenEs seien komplexe Zahlen, und eine reelle Zahl. Definiere die Exponentialsumme
Dann gilt für jedes die Abschätzung
Mit Hilfe dieser Integralungleichung können weitere Ungleichungen des folgenden Typs erhalten werden.[197] Ist eine Familie reeller Zahlen
wobei das eindeutige Element von in ist, gilt die Ungleichung (auch Das große Sieb genannt)[198]
Der Faktor kann in dieser Abschätzung nicht verbessert werden.[199] Aufgrund dieser Tatsache gilt die Ungleichung als scharf und sehr mächtig. Das große Sieb hat zahlreiche Anwendungen in der analytischen Zahlentheorie, siehe auch Siebtheorie.
Bohr-Ungleichung
BearbeitenIm Jahr 1914 konnte Harald Bohr zeigen, dass falls die Potenzreihe in der Einheitskreisscheibe konvergiert und die holomorphe Funktion in erfüllt, bereits
gilt.[200] Dass sogar gilt und der größtmögliche Bohr-Radius ist, konnte unabhängig von Friedrich Wilhelm Wiener, Marcel Riesz und Issai Schur gezeigt werden.
Dualitätsprinzip
BearbeitenFür Einträge einer -Matrix und eine reelle Zahl sind die folgenden Aussagen äquivalent:[201]
- , für alle komplexen Zahlen ,
- , für alle komplexen Zahlen ,
- , für alle komplexen Zahlen .
Dies wird auch als Dualitätsprinzip bezeichnet.[202] Eine Folgerung dessen ist die Existenz einer von den abhängigen Konstanten , sodass für alle
wobei . Dabei steht für das Supremum.
Weitere Ungleichungen
BearbeitenDon Zagier zeigte die Ungleichung
mit positiven Zahlen , und .[203] Verwandt hierzu ist die für reelle Zahlen gültige Ungleichung
die 2003 auch eine Aufgabe in der Internationalen Mathematik-Olympiade war.[204]
Sind positive Zahlen und eine Permutation, so gilt[205]
Zudem gilt die Carleman-Ungleichung
mit der Eulerschen Zahl .
Spezielle Reihen
BearbeitenNeben der Konvergenz und dem numerischen Wert einer Reihe ist auch der symbolische Wert einer Reihe von Bedeutung. Beispielsweise lassen sich so mathematische Konstanten darstellen und numerisch berechnen. Für wichtige Reihendarstellungen existieren zudem Tabellierungen in Reihentafeln.
Geometrische Reihe
Bearbeiten
Es gilt für alle Werte und die Formel
Daraus ergibt sich für die geometrische Reihe[206]
Eine sehr weitreichende Verallgemeinerung der geometrischen Reihe sind die hypergeometrischen Reihen.
Harmonische Reihe
BearbeitenDie harmonische Reihe
ist divergent. Dies ist ein Beispiel dafür, dass das Nullfolgenkriterium für Konvergenz nur notwendig, aber nicht hinreichend ist. Die Divergenz ist von „logarithmischer Geschwindigkeit“, dies sieht man zum Beispiel durch
Es wurde jedoch die Frage untersucht, was passiert, wenn man die harmonische Reihe „ausdünnt“, also systematisch Summanden weglässt. Man spricht dann von subharmonischen Reihen. Leonhard Euler zeigte, dass auch, wenn man sich nur auf die Menge der Primzahlen beschränkt, immer noch Divergenz vorliegt. Viggo Brun gelang zu Beginn des 20. Jahrhunderts ein Durchbruch, indem er zeigte, dass bei erneuter Einschränkung auf die Komponenten und von Primzahlzwillingen , die Reihe konvergent ist:[207]
Der Grenzwert dieser Reihe ist auch als Brunsche Konstante bekannt. Die Frage, ob Konvergenz nach Wegstreichen von Zahlen mit bestimmten Ziffern in ihrer Dezimalschreibweise vorliegt, ist Gegenstand der Kempner-Reihen. Es kann damit Konvergenz erreicht werden.
Darstellung mathematischer Konstanten
BearbeitenKreiszahl
BearbeitenEs wurden neben der Leibniz-Reihe
zahlreiche weitere, teils sehr schnell konvergente, Reihendarstellungen für die Kreiszahl gefunden. Von historischer Bedeutung ist etwa das Basler Problem, das nach dem Grenzwert der Reihe aller reziproken Quadratzahlen fragte. Leonhard Euler publizierte 1735 in seiner De Summis Serierum Reciprocarum die Lösung:
Euler konnte allgemein für sogar[208]
mit den Bernoulli-Zahlen zeigen. Der Fall ungerader Exponenten ist deutlich schwieriger, und es existieren hier keine geschlossenen Analoga. Allerdings konnte Matyáš Lerch im Jahr 1900 folgende Reihenidentität aufzeigen:[209]
Während all diese Reihen vergleichsweise langsam konvergieren, ist die 1914 von Srinivasa Ramanujan veröffentlichte, auf Untersuchungen von elliptischen Funktionen und Modulfunktionen basierende Gleichung zur Berechnung der Kreiszahl gut geeignet:[210][211]
Die Brüder David und Gregory Chudnovsky berechneten mit ihrer Hilfe 2 Milliarden Nachkommastellen von in den frühen neunziger Jahren.[212] Der davon inspirierte Chudnovsky-Algorithmus basiert auf der folgenden verwandten Reihendarstellung:[213]
1995 entdeckte Simon Plouffe zusammen mit Peter Borwein und David Harold Bailey die Bailey-Borwein-Plouffe-Formel:
Diese Reihe ermöglicht es, die -te Stelle einer binären, hexadezimalen oder einer zu einer beliebigen anderen Zweierpotenz als Basis gehörenden Darstellung von zu berechnen, ohne dass zuvor die vorherigen Ziffernstellen berechnet werden müssen.[214]
Eulersche Zahl
BearbeitenDie Eulersche Zahl ist die Basis des natürlichen Logarithmus. Ihre bekannteste Reihendarstellung ergibt sich aus der Taylor-Entwicklung der natürlichen Exponentialfunktion:[215]
Aufgrund ihrer schnellen Konvergenz ist diese Reihe nicht nur zur Berechnung von Dezimalstellen der Eulerschen Zahl geeignet. Es kann mit ihrer Hilfe auch ein elementarer Beweis erbracht werden, dass eine irrationale Zahl ist.[216] Allerdings reicht die Konvergenzgeschwindigkeit bei Weitem nicht aus, die Transzendenz von nachzuweisen (im Gegensatz etwa zur Liouville-Zahl), und für den Beweis dieser Aussage sind speziellere Techniken vonnöten.[217]
Weitere Konstanten
BearbeitenFür zahlreiche weitere mathematische Konstanten existieren diverse Reihendarstellungen. Zum Beispiel geht die Reihendarstellung
mit den zentralen Binomialkoeffizienten auf Isaac Newton zurück.[218]
Roger Apéry nutzte im Jahr 1979 die Reihe
um die Irrationalität von , der Apéry-Konstante, zu zeigen.[219] Es gilt hingegen auch
Reihen dieser Art werden auch als Apéry-Reihen bezeichnet.[220] In dem Wunsche, Apérys Beweismethode gegebenenfalls auch auf andere Zeta-Werte anwenden zu können, sind diese bis heute Gegenstand intensiver Forschung. Beiträge lieferten unter anderem Ablinger, Bailey, Borwein, Sun und Zucker.[221][222][223][224] Beim Versuch einer Verallgemeinerung stößt man natürlicherweise auf Verbindungen zu allgemeinen harmonischen Summen und multiplen Polylogarithmen. Doch trotz Formeln wie zum Beispiel[225]
steht der Durchbruch bis heute aus. In diesem Kontext ist auch die Reihe
mit dem natürlichen Logarithmus des Goldenen Schnittes bemerkenswert.[226]
Reihen mit rationalen Gliedern sind für die Euler-Mascheroni-Konstante vergleichsweise schwer zu finden. Ein berühmtes Beispiel ist eine von Giovanni Enrico Eugenio Vacca gegebene Reihe
aus dem Jahr 1910.[227] Es bedeutet die Gaußklammer.
Summenformeln und Transformationen
BearbeitenPartielle Summation
BearbeitenSind die Glieder von Reihen, bzw. ihrer Partialsummen, von der Gestalt , so kann durch Umordnung „partiell summiert“ werden. Etwa gilt für und [228]
- wobei .
Dies bezeichnet man auch als Abelsche partielle Summation. Bestätigen lässt sich dies durch sukzessives Ausmultiplizieren und Verrechnen der Terme. Trotz ihrer Einfachheit erweist sich die partielle Summation als sehr hilfreich in vielen Situationen. Sie kommt vor allem dann zum Einsatz, wenn die Zahlen „schwanken“ (etwa ständige Vorzeichenwechsel), womit deren Summen verhältnismäßig klein sind, während die Zahlen sukzessive kleiner werden, da dann die Differenzen eventuell viel schneller gegen Null streben als die selbst. Zum Beispiel ist sie dazu geeignet, die Existenz einer Abszisse bedingter Konvergenz für Dirichletreihen zu zeigen.
Eine Variante der partiellen Summation ist die Identität[229]
Eine weitere Variante betrifft den Fall, dass mit einem auf dem Intervall stetig differenzierbaren . Dann gilt mit [230]
Diese Transformation ist dann hilfreich, wenn durch „Schwankungen“ der Summanden verhältnismäßig klein ist, während „schnell“ gegen Null geht. Ein Beispiel ist , dessen Ableitung für sogar quadratisch gegen Null strebt.
Integralvergleich
BearbeitenIst eine reellwertige, monotone Funktion auf dem Intervall mit ganzen , so existiert eine Konstante , sodass[231]
Euler-Maclaurin-Formel
BearbeitenEine Möglichkeit, eine Reihe auszuwerten oder anzunähern, bietet die Euler-Maclaurin-Summenformel. Diese drückt Summen explizit in der Sprache der Integralrechnung aus und ist allgemein gegeben durch:
Hierbei ist eine auf dem Intervall mindestens -mal differenzierbare Funktion und eine natürliche Zahl. Es bezeichnen zudem die Bernoulli-Zahlen, die Bernoulli-Polynome und den ganzzahligen Anteil von .[232] Die ersten Formen haben die Gestalt: wobei abkürzend .
Eine Anwendung dieser Summenformel ist die effiziente Berechnung der Partialsummen konvergenter oder auch divergenter Reihen. Ein Beispiel ist die harmonische Reihe:
mit der Euler-Mascheroni-Konstanten und einer beschränkten Folge .[233] Zum Beispiel ist
- und
Abel-Plana-Summenformel
BearbeitenÄhnlichkeit zur Euler-Maclaurin-Summenformel hat die Abel-Plana-Summenformel. Sei holomorph für mit und . Man nehme an, dass
gleichmäßig für . Dann gilt[234]
Die Poissonsche Summationsformel
BearbeitenKlassisch
BearbeitenGelten für geeignete Wachstumsbedingungen, ist es zum Beispiel eine Schwartz-Funktion, so gilt ferner die Poissonsche Summenformel:
Diese ermöglicht es, eine Reihe über Funktionswerte an ganzen Stellen in jene bezüglich der Fourier-Transformierten
umzuwandeln, und umgekehrt.[235] Benutzt wird diese Summenformel unter anderem beim Nachweis der Transformationsformel für die Jacobische Theta-Reihe.
Verwandt dazu ist der folgende Satz. Ist mit , und eine stetige Funktion mit endlicher Variation auf , die über integrierbar ist, so gilt für[236]
bereits
Verallgemeinerungen
BearbeitenDie Poisson’sche Summationsformel kann sehr weitreichend verallgemeinert werden. Zu Grunde liegen Folgen , die besondere Eigenschaften mitbringen müssen:
- Die zugehörige Dirichlet-Reihe konvergiert für alle mit , besitzt eine holomorphe Fortsetzung nach und hat einen Pol der Ordnung in .
- Die Komplettierung erfüllt eine Funktionalgleichung , wobei eine andere – zu „duale“ – Folge ist und eine komplexe Zahl mit . Es ist zudem für positive (mit der Gammafunktion ) ein sog. „Gammafaktor“, und für wird all dies analog definiert (mit Gammafaktor etc.).
Gelten dann alle Notationen wie oben, und setzt man für
- und
so gilt
vorausgesetzt, alle Ausdrücke konvergieren. Es bezeichnet dabei das Residuum an der Stelle .
Beispiele für diesen Formalismus sind:
Ist , so gilt mit der Riemannschen Zeta-Funktion. Setzt man , ist diese wegen ihrer Funktionalgleichung selbst-dual. Es gilt ferner
aber gleichzeitig auch
mit dem Eulerschen Ergänzungssatz sowie der Duplikationsformel für die Gammafunktion. Damit ergibt sich und für gerade Funktionen
was eine Variante der Poisson’schen Summationsformel ist.[237]
Van der Corputsche Summenformel
BearbeitenSei vorgegeben. Dann gibt es eine Konstante mit folgender Eigenschaft: Für seien und stetig differenzierbare Funktionen. Es seien , und monoton fallend. Dann gilt[238]
mit der Restgliedabschätzung
Perronsche Formel
BearbeitenDie Perronsche Formel behandelt Folgen , die höchstens polynomiell anwachsen. Sie stellt eine Verbindung der Partialsummen zu der Dirichlet-erzeugenden Funktion über Kurvenintegrale her.
Es sei eine Dirichlet-Reihe, die irgendwo konvergiert, ihre Konvergenzabszisse. Für jedes definiert man die summatorische Funktion
wobei für alle nicht-natürlichen einfach 0 ist. Dann gilt für die Formel
wobei das Integral im Falle von bedingt konvergiert und für im Sinne des Cauchyschen Hauptwertes existiert.[239]
Mellintransformation
BearbeitenSrinivasa Ramanujan, der für seine starke analytische Intuition bekannt ist, machte laut Godfrey Harold Hardy „intensiven Gebrauch“ von der Formel[240]
Eine äquivalente Form ist
Dabei bezeichnet die Gammafunktion. Diese Identitäten sind jedoch nur formal zu verstehen, und Konvergenz liegt nur unter bestimmten Voraussetzungen vor. Hardy gab schließlich strenge Kriterien:[241] Es sei und , wobei fest gewählt ist. Man nehme an, dass holomorph im Bereich ist, und es Konstanten und gibt mit
für alle . Für und definiere man
Im Fall gilt die Reihendarstellung
Dann gilt für
Allgemeiner ist die Mellintransformation in der Lage, Potenzreihen in Dirichletreihen überzuführen.[242]
Möbiussche Umkehrformel
BearbeitenSind und reell- oder komplexwertige Funktionen auf , und ist
- (für alle ),
so lässt sich aus „rekonstruieren“ durch[243]
- (für alle ).
Dabei bezeichnet die Möbiusfunktion aus der Zahlentheorie. Die Summationsschranken können unter der Fortsetzung von und auf via für alle weggelassen werden. In diesem Fall folgt aus stets .
Eine Variante dieser Umkehrformel betrifft Dirichletreihen. Es gilt
- (für alle ) (für alle )
für alle , sodass beide Reihen für alle absolut konvergieren.
Reihentransformationen
BearbeitenEs zeigte Sarvadaman Chowla eine Identität zwischen Reihen periodischer Funktionen. Ist eine Folge mit , so gilt für fast alle reellen (also alle bis auf Nullmenge)
wobei mit .[244] Es bedeutet die Gaußklammer. Ein Spezialfall dieser Identität ist, mit und für alle ,
In manchen Fällen kann Konvergenz beschleunigt werden. Dazu kann die Reihe in eine andere transformiert werden. Ein Beispiel ist die Eulersche Reihentransformation. Ist
eine beliebige konvergente Reihe, so ist stets[245]
Eine Anwendung ist[246]
Asymptotische Analysis und Taubersätze
BearbeitenAsymptotik von Reihen mit holomorphen Gliedern
BearbeitenIn manchen Anwendungen ist es vonnöten, Reihen der Gestalt für (in einem Winkelbereich) zu verstehen. Erfüllt gewisse Eigenschaften, darunter Holomorphie, kann dies bewerkstelligt werden. Im Folgenden sei stets mit einem .
Es sei nun eine Funktion, die in einer Umgebung von holomorph ist, insbesondere im Ursprung. Ferner gebe es für jedes ein , sodass wenn in . Dann gilt für alle und :
gleichmäßig, sofern in .[247] Dabei bezeichnen die Bernoulli-Polynome und das Landau-Symbol (die Konstante hängt nur von der Wahl von ab). Die Aussage lässt sich sogar auf den Fall verallgemeinern, dass einen einfachen Pol im Ursprung mit Residuum hat. Gelten sonst alle Voraussetzungen wie oben, so gilt in dieser Situation für
gleichmäßig, sofern in .[248]
Taubersatz von Wiener-Ikahara
BearbeitenDer Satz von Wiener-Ikahara trifft manchmal Aussagen über Summen , wenn die Reihe gewisse Eigenschaften hat. Im Jahre 1954 konnte Delange den Satz von Wiener-Ikehara deutlich verallgemeinern, nämlich auf Singularitäten gemischten Typs.[249] Es sei eine Dirichlet-Reihe mit nicht-negativen Koeffizienten, die auf einer Halbebene konvergiert. Man nehme an, lasse sich mit Ausnahme des Punktes holomorph auf die gesamte Gerade fortsetzen und dass es sich in einer kleinen Umgebung um in der Form
schreiben lässt, wobei eine reelle Zahl und die Funktionen und holomorph sind mit . Dann gilt: Ist keine negative ganze Zahl, so folgt
und ist es eine negative ganze Zahl und :
Dabei bedeutet das Symbol , dass beide Seiten für wachsende Werte asymptotisch gleich schnell anwachsen, ihr Quotient also für gegen 1 strebt.
Weitere Anwendungen
BearbeitenUnendliche Produkte
BearbeitenEin unendliches Produkt wird, analog zur unendlichen Reihe, als Folge der Partialprodukte
definiert. Allerdings ist der Konvergenzbegriff für unendliche Produkte subtiler; es ist als Grenzwert nur zugelassen, falls ab einem gewissen die Partialprodukte für gegen einen Grenzwert konvergieren. Durch Logarithmusbildung bzw. Exponenzierung besteht ein Zusammenhang zwischen unendlichen Produkten und Reihen. So ist ein unendliches Produkt
genau dann absolut konvergent (bzw. unbedingt konvergent, der Grenzwert hängt also nicht von der Reihenfolge der Faktoren ab), falls die Reihe absolut konvergiert.[250][251] konvergiert, falls und konvergieren. Andererseits kann besagtes Produkt unter Umständen bedingt konvergieren, selbst wenn und beide divergieren.[252]
Wahrscheinlichkeitstheorie
BearbeitenIn der Wahrscheinlichkeitstheorie sind unendliche Reihen unter anderem im Kontext mit stochastischen Prozessen von Bedeutung. Ein Resultat in dieser Richtung ist etwa der kolmogoroffsche Dreireihensatz.[253] Das asymptotische Verhalten der Partialsummen der unendlichen Reihe mit gewissen identisch verteilten Zufallsvariablen ist Gegenstand des Gesetzes der großen Zahlen[254] und des zentralen Grenzwertsatzes.[255] Allerdings tauchen sie bereits bei der Axiomatisierung der Wahrscheinlichkeitstheorie durch Kolmogoroff auf: Darin wird verlangt, dass ein Wahrscheinlichkeitsmaß für eine abzählbare Folge von disjunkten Ereignissen eines Wahrscheinlichkeitsraums stets
erfüllen muss. Die Reihe zur Rechten ist dabei stets absolut konvergent mit einem Grenzwert in , da das Maß nicht-negativ und monoton ist und zudem verlangt wird.[256] Eine Verallgemeinerung auf Ebene endlicher Vereinigungen ist die Inklusions-/Exklusionsformel, die für beliebige Ereignisse gilt:[257]
In Kontexten der probabilistischen Zahlentheorie untersuchte unter anderem Emmanuel Kowalski Zufallsreihen.[258]
Finanzmathematik
BearbeitenAnnuitätendarlehen sind das gängigste Modell zur Finanzierung privater Immobilien. Zwischen Kreditgeber und -nehmer werden ein Zinssatz, eine monatlich zu zahlende Rate und eine Laufzeit vereinbart. Am Ende der Laufzeit bleibt eine Restschuld, für die dann ein neuer Kreditvertrag abgeschlossen wird, wobei die Zinsrate an die aktuelle Geldmarktsituation angepasst wird. Um das Risiko zu kennen, ist es ergo für jeden Hausbauer wichtig, die Restschuld zu bestimmen.[259]
Es bezeichnen die Kreditsumme, die monatliche Rate und die jährliche Zinsrate. Die nach Monaten noch verbleibende Restschuld sei . Die im -ten Monat zu entrichtenden Zinsen werden im Bankwesen zu bestimmt. Die folgen mit der Rekursion
Unter Betrachtung der erzeugenden Funktion der kann unter Ausnutzung dieser Rekursion
gezeigt werden, und durch einige Umformungen erhält man
Durch Koeffizientenvergleich erhält man damit die geschlossene Formel[259]
Zahlentheorie
BearbeitenReihen haben auch bedeutende Anwendung in der analytischen Zahlentheorie. So kann es in vielen Fällen helfen, einer zu untersuchenden zahlentheoretischen Funktion die erzeugenden Funktionen
- oder
zuzuordnen. Mit Hilfe von Tauber-Sätzen,[260] Integraltransformationen (wie der Perronschen Formel)[261] oder der Kreismethode[262] können dann gegebenenfalls detaillierte Aussagen über das langfristige Verhalten der getroffen werden. Handelt es sich bei sogar (im Wesentlichen) um eine Modulform, kann in bestimmten Fällen eine exakte Formel in Form einer unendlichen Reihe für die hergeleitet werden. Dies ist etwa bei der Partitionsfunktion der Fall:[263]
wobei die Bessel-Funktion und eine sog. Kloosterman-Summe bezeichnet.
Auch bei Dichteresultaten, etwa im Umfeld der Duffin-Schaeffer-Vermutung oder des Satzes von Green-Tao, spielen unendliche Reihen eine zentrale Rolle. Die Duffin-Schaeffer-Vermutung besagt, dass für jede Funktion die Ungleichung
für fast alle (im Sinne des Lebesgue-Maßes) für unendlich viele teilerfremde lösbar ist, genau dann, wenn[264]
Dabei ist die Eulersche Phi-Funktion. Gilt hingegen , so ist die entsprechende Ungleichung fast sicher nicht unendlich oft erfüllt.[265] Aus probabilistischer Sicht handelt es sich um ein Null-Eins-Gesetz. Während diese letzte Richtung über Argumente des Borel-Cantelli-Lemmas recht schnell ersichtlich ist, galt die andere Richtung, also aus der Reihendivergenz die fast sichere unendlich frequentierte Lösbarkeit zu folgern, lange als extrem schwieriges zahlentheoretisches Problem. Ein vollständiger Beweis der Vermutung konnte erst 2019 durch Dimitris Koukoulopoulos und James Maynard erbracht werden. Eine Abschwächung der Vermutung war bereits als Satz von Chintschin bekannt, wobei die Beweise hier vergleichsweise elementar sind.[266] Darüber hinaus „messen“ Reihen in gewisser Weise „ab“, wie dicht gewisse arithmetische Objekte, etwa Primzahlen, in anderen Objekten verteilt sind. Verwandt zum Satz von Green-Tao, der besagt, dass die Folge der Primzahlen beliebig lange arithmetische Progressionen enthält, ist eine Vermutung von Paul Erdős. Sie sagt aus, dass eine Folge natürlicher Zahlen mit der Eigenschaft
bereits beliebig lange arithmetische Progressionen enthalten muss. Diese weit offene Vermutung würde zusammen mit dem Satz von Euler, , den Satz von Green-Tao implizieren.[267]
Bereits der im 19. Jahrhundert bewiesene Dirichletsche Primzahlsatz kann über die Divergenz bestimmter unendlicher Reihen formuliert werden. Dirichlet konnte nachweisen, dass für teilerfremde und [268]
und verifizierte sogar das noch stärkere Resultat
für zu teilerfremde und .[269] Trivialerweise implizieren diese Resultate die Aussage, dass es unendlich viele Primzahlen in der entsprechenden arithmetischen Progression gibt, wobei letzteres Resultat sogar auf eine Form der „Gleichverteilung“ hinweist.
Anmerkungen
Bearbeiten- ↑ Aus Gründen der Einfachheit wird davon ausgegangen, dass sowohl Achilles als auch die Schildkröte mit konstanter Geschwindigkeit laufen.
- ↑ In manchen Anwendungen ist es zweckmäßig, den Summenindex bei anderen Werten wie zum Beispiel beginnen zu lassen.
- ↑ Die (lokale) Integrierbarkeit von folgt hier bereits mit der geforderten Monotonie.
Literatur (Auswahl)
Bearbeiten- Herbert Amann, Joachim Escher: Analysis III. Zweite Auflage, Birkhäuser, Basel 2008, ISBN 978-3-7643-8883-6.
- Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Springer Spektrum, Berlin/Heidelberg 2022, ISBN 978-3-662-64388-4.
- Edwin F. Beckenbach, Richard Bellmann: Inequalities. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 30, Second Revised Printing, Springer-Verlag, Berlin / Heidelberg / New York 1965.
- Ludmila Bourchtein, Andrei Bourchtein: Theory of Infinite Sequences and Series. Birkhäuser, Cham 2022, ISBN 978-3-030-79430-9.
- Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer-Verlag, Berlin Heidelberg 1995, ISBN 3-540-58821-3.
- Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s (= Sources and Studies in the History of Mathematics and Physical Sciences.). Springer, New York (NY) 2008, ISBN 978-0-387-73467-5.
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1. Springer-Verlag, 1993/ 4., korrigierte und erweiterte Auflage, Springer Spektrum, Berlin 2006, ISBN 3-540-31764-3.
- Izrail Solomonovic Gradshteyn, Iosif Mojseevic Ryzhik: Table of Integrals, Series and Products. Herausgegeben von Alan Jeffrey und Daniel Zwillinger. 7. Ausgabe. Elsevier Academic Press, Amsterdam u. a. 2007, ISBN 978-0-12-373637-6.
- Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Springer-Verlag, Berlin u. a. 1996, ISBN 3-540-59111-7 (Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 2).
- Jacob Korevaar: Tauberian Theory. A century of developments (= Grundlehren der mathematischen Wissenschaften.). Springer-Verlag, Berlin / Heidelberg / New York 2004, ISBN 3-540-21058-X.
- D. Mitrinovic: Analytic inequalities. Die Grundlehren der mathematischen Wissenschaften Band 165, Springer-Verlag, Berlin / Heidelberg / New York 1970, ISBN 978-3-642-99972-7.
- Anil Nerode, Noam Greenberg: Algebraic Curves and Riemann Surfaces for Undergraduates. Springer-Verlag, Switzerland 2022, ISBN 978-3-031-11615-5.
- Marius Overholt: A Course in Analytic Number Theory. (= Graduate Studies in Mathematics. Band 160). American Mathematical Society, Providence (R.I.) 2014, ISBN 978-1-4704-1706-2.
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 1 (= Springer-Lehrbuch.). 5., neu bearbeitete Auflage, Springer-Verlag, Berlin/Heidelberg 2002, ISBN 3-540-41855-5.
- Thomas Sonar: 3000 Jahre Analysis. Geschichte – Kulturen – Menschen. 2. Auflage. Springer, Berlin 2016, ISBN 978-3-662-48917-8.
- Terence Tao: Analysis I (= Text and Readings in Mathematics.). Third Edition, Hindustan Book Agency, New Delhi 2006, ISBN 978-93-80250-64-9.
- Terence Tao: Analysis II (= Texts and readings in mathematics.). Third Edition, Hindustan Book Agency, New Delhi 2006, ISBN 978-93-80250-65-6.
- K. Zeller, W. Beekmann: Theorie der Limitierungsverfahren (= Ergebnisse der Mathematik und ihrer Grenzgebiete. Band 15). Springer-Verlag, Berlin / Heidelberg / New York 1970.
- Tian-Xiao He: Methods for the Summation of Series. Chapman & Hall (CRC Press), Boca Raton / London / New York 2022, ISBN 978-0-367-50797-8, doi:10.1201/9781003051305.
Weblinks
BearbeitenEinzelnachweise
Bearbeiten- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 180–181.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 181.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 301.
- ↑ Richard Isaac: The Pleasures of Probability. Springer Verlag New York, 1995, S. 44–46.
- ↑ Vgl. William Feller: An Introduction to Probability Theory and its Applications. Wiley, 3rd Edition, New York / London / Sydney, 1968, S. 265–266.
- ↑ Summenfolge. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
- ↑ Wolfgang Stegmüller: Neue Betrachtungen über Aufgaben und Ziele der Wissenschaftstheorie. Wahrscheinlichkeit – Theoretische Begriffe – Induktion. Das ABC der modernen Wahrscheinlichkeitstheorie und Statistik. Springer-Verlag, 2013, ISBN 978-3-642-61952-6, S. 147 (google.com [abgerufen am 5. März 2024]).
- ↑ Hubert Weber, Helmut Ulrich: Laplace-Transformation: Grundlagen – Fourierreihen und Fourierintegral – Anwendungen. 8. Auflage. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0140-1, S. 92 (google.com [abgerufen am 5. März 2024]).
- ↑ Reihe. In: Guido Walz (Hrsg.): Lexikon der Mathematik. 1. Auflage. Spektrum Akademischer Verlag, Mannheim/Heidelberg 2000, ISBN 3-8274-0439-8.
- ↑ a b Herbert Amann, Joachim Escher: Analysis 1 (= Grundstudium Mathematik.). 3. Auflage, Birkhäuser, Basel 2006, ISBN 3-7643-7756-9, S. 195.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 244.
- ↑ Otto Forster: Analysis. Band 1: Differential- und Integralrechnung einer Veränderlichen. 8., verbesserte Auflage, Springer Spektrum, Wiesbaden 2006, ISBN 3-528-67224-2, S. 37.
- ↑ a b Terence Tao: Analysis 1. 3. Ausgabe, New Delhi 2006, S. 167.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 143–144.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 308.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 309.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage, Basel 2006, S. 208.
- ↑ Ilja Nikolaevic Bronstejn, Konstantin Adolfovic Semendjajew et al.: Taschenbuch der Mathematik. 6., vollständig überarbeitete und ergänzte Auflage, Harri Deutsch, Frankfurt am Main 2005, ISBN 3-8171-2006-0, S. 426.
- ↑ Anil Nerode, Noam Greenberg: Algebraic Curves and Riemann Surfaces for Undergraduates. Switzerland 2022, S. 292.
- ↑ Thomas William Körner: Fourier Analysis. Cambridge University Press, Cambridge 1988, ISBN 0-521-25120-6, S. 231.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 1.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 3.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 7–8.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 9.
- ↑ Euler: De summis serierum reciprocarum. In: Opera Omnia. Reihe I, Band 14, S. 73–86, in der Standard-Notation der Werke von Euler von Eneström ist das E 41, zuerst erschienen in Novi commentarii Academiae Scientiarum Imperialis Petropolitanae. (Comm. Acad. Petrop.) Ausgabe 7 (1734/35), St. Petersburg 1740, S. 123–134. Die Arbeit wurde im Dezember 1735 der Akademie vorgelegt.
- ↑ Thomas Sonar: 3000 Jahre Analysis. Springer-Verlag, Berlin/Heidelberg 2011, ISBN 978-3-642-17203-8, S. 383–385 (doi:10.1007/978-3-642-17204-5).
- ↑ Thomas Sonar: 3000 Jahre Analysis. Springer-Verlag, Berlin/Heidelberg 2011, S. 377.
- ↑ Thomas Sonar: 3000 Jahre Analysis. Springer-Verlag, Berlin/Heidelberg 2011, S. 377–378.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 25.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 26.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 27–28.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 87.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 137.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 141.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 146.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 147.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 153.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 151.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 155.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 159.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 195.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 193.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 171.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A Tricentennial Tribute. Imperial College Press, Singapore 2010, ISBN 978-1-84816-525-0, S. 217.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A Tricentennial Tribute. Singapore 2010, S. 202.
- ↑ Karl Zeller, Wolfgang Beekmann: Theorie der Limitierungsverfahren (= Ergebnisse der Mathematik und ihrer Grenzgebiete. 2. Folge). Reprint der 2. Auflage von 1970, Springer-Verlag, Berlin 2014, ISBN 978-3-642-88471-9, S. 3.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler: A Tricentennial Tribute. Singapore 2010, S. 209–210.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 233.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 231.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 290.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 311.
- ↑ Giovanni Ferraro: The Rise and Development of the Theory of Series up to the Early 1820s. New York (NY) 2008, S. 347.
- ↑ a b Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage, Berlin/Heidelberg 2002, S. 3.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 458.
- ↑ Harold Mortimer Edwards: Riemann’s Zeta Function. Academic Press, New York 1974, ISBN 0-12-232750-0, S. 9.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 328.
- ↑ Elias Stein, Rami Shakarchi: Complex analysis (= Princeton lectures in analysis.). Princeton University Press, Princeton (NJ) 2003, ISBN 0-691-11385-8, S. 113.
- ↑ K. Zeller, W. Beekmann: Theorie der Limitierungsverfahren. Berlin 2014, S. 3–4.
- ↑ K. Zeller, W. Beekmann: Theorie der Limitierungsverfahren. Berlin 2014, S. 4 ff.
- ↑ Srinivasa Ramanujan Aiyangar, Bruce C. Berndt: Ramanujan’s Notebooks Part I. E-Book, Springer Science+Business Media, New York 1985, ISBN 1-4612-1088-7, S. 133.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part II. E-Book, Springer-Verlag, New York 1989, ISBN 1-4612-4530-3, S. 248.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part II. New York 1989, S. 253.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part II. New York 1989, S. 240.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 1 ff.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York, S. 133–134.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 1.
- ↑ Andrei Nikolajewitsch Kolmogorow: Une série de Fourier–Lebesgue divergente presque partout. In: Fundamenta Mathematicae. 1923, Band 4, Nr. 1, S. 324–328, ISSN 0016-2736, hier S. 32.
- ↑ Lennart Carleson: On convergence and growth of partial sums of Fourier series. In: Acta Mathematica. Band 116, 1966, S. 135–157.
- ↑ Eberhard Freitag: Funktionentheorie 2. Springer-Verlag, Berlin/Heidelberg 2009, S. 311.
- ↑ E. Freitag: Funktionentheorie 2. Berlin/Heidelberg 2009, S. 326 ff.
- ↑ Edmond D. Cashwell, C. J. Everett: The ring of number-theoretic functions. In: Pacific Journal of Mathematics. 1959, Band 9, Nr. 4, S. 975–985 (doi:10.2140/pjm.1959.9.975).
- ↑ Krishnaswami Alladi: Ramanujan’s Place in the World of Mathematics: Essays Providing a Comparative Study. Springer-Verlag, New Delhi 2013, S. 122 (eingeschränkte Buchvorschau auf google-books, abgerufen am 5. März 2024).
- ↑ George E. Andrews: The Theory of Partitions (= Encyclopedia of mathematics and its applications.). Cambridge University Press, Cambridge 1984, ISBN 0-521-30222-6, S. 16 ff.
- ↑ Lokenath Debnath: The legacy of Leonhard Euler. A Tricentennial Tribute. Imperial College Press, S. xvii.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory: from Euclid to Hardy and Littlewood (= Springer Monographs in Mathematics.). Springer-Verlag, Berlin/Heidelberg 2000, ISBN 3-540-66289-8, S. 158.
- ↑ Marius Overholt: A Course in Analytic Number Theory. (= Graduate Studies in Mathematics. Band 160). American Mathematical Society, Providence (R.I.) 2014, ISBN 978-1-4704-1706-2, S. 52.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 135–136.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 262.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 330.
- ↑ Edwin F. Beckenbach, Richard Bellmann: Inequalities. Berlin / Heidelberg / New York 1965, S. 117.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 148.
- ↑ a b Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 134.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 139.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 263.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage, Frankfurt am Main 2005, S. 430.
- ↑ Terence Tao: Analysis II. Texts and Readings in Mathematics, Hindustan Book Agency, S. 53.
- ↑ Terence Tao: Analysis II. New Delhi 2006, S. 54.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage, Frankfurt am Main 2005, S. 432.
- ↑ Herbert Amann, Joachim Escher: Analysis III. Zweite Auflage, Basel 2008, S. 110.
- ↑ Herbert Amann, Joachim Escher: Analysis III. Zweite Auflage, Basel 2008, S. 104.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 101.
- ↑ Terence Tao: Analysis II. New Delhi 2006, S. 101.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 151 ff.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage, Frankfurt am Main 2005, S. 435.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage, Springer, Berlin/Heidelberg 2002, S. 189.
- ↑ Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage, Springer, Berlin/Heidelberg 2002, S. 190.
- ↑ E. Stein, R. Shakarchi: Complex analysis. Princeton (NJ) 2003, S. 34.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage, Frankfurt am Main 2005, S. 439.
- ↑ Thomas William Körner: Fourier Analysis. Cambridge University Press, Cambridge 1988, ISBN 0-521-25120-6, S. 33.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 299.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 149.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 148.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 335.
- ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers. In: Graduate studies in mathematics. Band 203. American Mathematical Society, Providence (RI) 2020, ISBN 978-1-4704-4754-0, S. 57.
- ↑ George Pólya, Gábor Szegö: Aufgaben und Lehrsätze aus der Analysis. Band 1: Reihen – Integralrechnung – Funktionentheorie (= Die Grundlehren der mathematischen Wissenschaften. Band 19). 3., berichtigte Auflage, Springer-Verlag, Berlin 1964, S. 116–117.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 268.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 257.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 271–272.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 322.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 125.
- ↑ Serge Lang: Undergraduate Analysis (= Undergraduate texts in mathematics.). 2. Edition, Springer-Verlag, New York 1997, ISBN 0-387-94841-4, S. 209.
- ↑ Terence Tao: Analysis 1. 3. Ausgabe, New Delhi 2006, S. 181.
- ↑ Terence Tao: Analysis 1. 3. Ausgabe, New Delhi 2006, S. 179.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage, Basel 2006, S. 223.
- ↑ a b c Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 324.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 297.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 412.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage, Basel 2006, S. 198.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 125.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 276.
- ↑ Serge Lang: Undergraduate Analysis. 2. Edition, New York 1997, S. 210.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 325.
- ↑ Terence Tao: Analysis 1. 3. Ausgabe, New Delhi 2006, S. 172.
- ↑ P. D. T. A. Elliott: Probabilistic Number Theory I (= Grundlehren der mathematischen Wissenschaften. Band 239). Springer, S. 333–334.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 10.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 14.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 54.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 192.
- ↑ Hugh L. Montgomery, Robert C. Vaughan: Multiplicative Number Theory I. Classical Theory (= Cambridge studies in advanced mathematics.). Cambridge University Press, Cambridge 2006, ISBN 978-1-107-40582-0, S. 161.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory. AMS, 1990, S. 357.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 172.
- ↑ Gerald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory (= Graduate Studies in Mathematics. Band 163). 3. Edition, American Mathematical Society, Providence (RI) 2015, ISBN 978-0-8218-9854-3, S. 343.
- ↑ Gerald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory (= Graduate Studies in Mathematics. Band 163). 3. Edition, American Mathematical Society, Providence (RI) 2015, ISBN 978-0-8218-9854-3, S. 344.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 4.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 11.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 148.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 153.
- ↑ Jacob Korevaar: Tauberian Theory. A century of developments. Berlin / Heidelberg / New York 2004, S. 133–134.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 241.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 242.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 243.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 244.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 220.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 218–219.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 256–257.
- ↑ Tsuneo Arakawa, Tomoyoshi Ibukiyama, Masanobu Kankeo: Bernoulli Numbers and Zeta Functions. Springer Monographs in Mathematics, Springer Japan, 2014, S. 28–29.
- ↑ Jörg Arndt, Christoph Haenel: Pi. Algorithmen, Computer, Arithmetik. 2., überarbeitete und erweiterte Auflage, Springer-Verlag, Berlin/Heidelberg 2000, ISBN 978-3-540-66258-7, S. 69–70.
- ↑ David H. Bailey, Peter B. Borwein, Simon Plouffe: On the Rapid Computation of Various Polylogarithmic Constants. In: Mathematics of Computation. Band 66, Nr. 218, 1997, S. 903–913.
- ↑ James D. Harper: Another simple proof of . In: American Mathematical Monthly. Band 110, Nr. 6, 2003, S. 540–541.
- ↑ E. Stein, R. Shakarchi: Complex analysis. Princeton (NJ) 2003, S. 36.
- ↑ E. Stein, R. Shakarchi: Complex analysis. Princeton (NJ) 2003, S. 79–80.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 188.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part I. New York 1985, S. 96.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part I. New York 1985, S. 97.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 260.
- ↑ Dragoslav S. Mitrinovic, Josip E. Pečarić, Arlington M. Fink: Classical and new inequalities in analysis. Kluwer Academic Publishers, Dordrecht 1993, ISBN 0-7923-2064-6, S. 499.
- ↑ Dragoslav S. Mitrinovic, J. Pecaric, A. M. Fink: Classical and New Inequalities in Analysis. Dordrecht 1993, S. 500.
- ↑ Dragoslav S. Mitrinovic, J. Pecaric, A. M. Fink: Classical and New Inequalities in Analysis. Dordrecht 1993, S. 492.
- ↑ Dragoslav S. Mitrinovic, J. Pecaric, A. M. Fink: Classical and New Inequalities in Analysis. Dordrecht 1993, S. 506.
- ↑ Edwin F. Beckenbach, Richard Bellmann: Inequalities. Berlin / Heidelberg / New York 1965, S. 4.
- ↑ Herbert Amann, Joachim Escher: Analysis 2 (= Grundstudium Mathematik.). 2., korrigierte Auflage, Basel 2006, ISBN 3-7643-7105-6, S. 96.
- ↑ Herbert Amann, Joachim Escher: Analysis 2. 2., korrigierte Auflage, Basel 2006, S. 95–96.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage, Basel 2006, S. 199.
- ↑ Serge Lang: Undergraduate Analysis. 2. Edition, New York 1997, S. 217.
- ↑ Serge Lang: Undergraduate Analysis. 2. Edition, New York 1997, S. 220.
- ↑ Serge Lang: Undergraduate Analysis. 2. Edition, New York 1997, S. 222.
- ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. Providence (RI) 2015, S. 4.
- ↑ a b Kathrin Bringmann, Chris Jennings-Shaffer, Karl Mahlburg: On a Tauberian theorem of Ingham and Euler–Maclaurin summation. In: The Ramanujan Journal. 15. Mai 2021, doi:10.1007/s11139-020-00377-5, S. 18.
- ↑ Dragoslav S. Mitrinovic, J. Pecaric, A. M. Fink: Classical and New Inequalities in Analysis. Dordrecht 1993, S. 412–413.
- ↑ Dragoslav S. Mitrinovic, J. Pecaric, A. M. Fink: Classical and New Inequalities in Analysis. Dordrecht 1993, S. 413.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 226.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 226–227.
- ↑ E. Stein, R. Shakarchi: Complex analysis. Princeton (NJ) 2003, S. 49.
- ↑ Thomas William Körner: Fourier Analysis. Cambridge University Press, Cambridge 1988, ISBN 0-521-25120-6, S. 152.
- ↑ Robert B. Burckel: Classical Analysis in the Complex Plane. Birkhäuser, New York 2021, S. 296.
- ↑ Serge Lang: Undergraduate Analysis. 2. Edition, New York 1997, S. 214.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage, Frankfurt am Main 2005, S. 31.
- ↑ Dragoslav S. Mitrinovic, J. Pecaric, A. M. Fink: Classical and New Inequalities in Analysis. Dordrecht 1993, S. 89.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage, Frankfurt am Main 2005, S. 32.
- ↑ B. J. Venkatachala: Inequalities. An Approach Through problems. Hindustan Book Agency, New Dehli, 2009, S. 30.
- ↑ Bronstein, Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage, Frankfurt am Main 2005, S. 33.
- ↑ D. Mitrinovic: Analytic inequalities. Berlin / Heidelberg / New York 1970, S. 56–57.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 118.
- ↑ Terry Sheil-Small: Complex Polynomials. In: Cambridge Studies in advanced mathematics. Band 75, Cambridge University Press, Cambridge 2002, ISBN 0-521-40068-6, S. 129–130.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Berlin/Heidelberg 1995, S. 146.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 138.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 146–147.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 139.
- ↑ Emmanuel Kowalski: An Introduction to Probabilistic Number Theory. In: Cambridge studies in advanced mathematics. Band 192, S. 145.
- ↑ Hugh L. Montgomery: Ten lectures on the interface between analytic number theory and harmonic analysis. AMS, Providence 1994, S. 18.
- ↑ Hugh L. Montgomery: Ten lectures on the interface between analytic number theory and harmonic analysis. AMS, Providence 1994, S. 18–19.
- ↑ Ekkehard Krätzel: Analytische Funktionen in der Zahlentheorie. Teubner-Texte zur Mathematik, Stuttgart/Leipzig/Wiesbaden November 2000, S. 10.
- ↑ Ekkehard Krätzel: Analytische Funktionen in der Zahlentheorie. Teubner-Texte zur Mathematik, Stuttgart/Leipzig/Wiesbaden November 2000, S. 12.
- ↑ Ekkehard Krätzel: Analytische Funktionen in der Zahlentheorie. Teubner-Texte zur Mathematik, Stuttgart/Leipzig/Wiesbaden November 2000, S. 14.
- ↑ Ekkehard Krätzel: Analytische Funktionen in der Zahlentheorie. Teubner-Texte zur Mathematik, Stuttgart/Leipzig/Wiesbaden November 2000, Kapitel 4.
- ↑ Marius Overholt: A Course in Analytic Number Theory. Providence (R.I.) 2014, S. 132.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Berlin/Heidelberg 1995, S. 154–156.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Berlin/Heidelberg 1995, S. 159.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Berlin/Heidelberg 1995, S. 155.
- ↑ Harald Bohr: A theorem concerning power series. In: Proceedings of the London Mathematical Society. Band 13, Nr. 2, 1914, S. 1–5.
- ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. 3. Edition, Providence (RI) 2015, S. 74.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1995, S. 156–159.
- ↑ Dragoslav S. Mitrinovic, J. Pecaric, A. M. Fink: Classical and New Inequalities in Analysis. Dordrecht 1993, S. 584–585.
- ↑ B. J. Venkatachala: Inequalities. An Approach Through problems. Hindustan Book Agency, New Dehli, 2009, S. 203.
- ↑ B. J. Venkatachala: Inequalities. An Approach Through problems. Hindustan Book Agency, New Dehli, 2009, S. 211.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage, Basel 2006, S. 196–197.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 182.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 245–246.
- ↑ Matyáš Lerch: Sur la fonction ζ(s) pour les valeurs impaires de l’argument. In: Jornal de sciencias mathematicas e astronomicas. Band 14, 1900, S. 65–69 (französisch; Jahrbuch-Zusammenfassung), abgerufen am 5. März 2024.
- ↑ Srinivasa Ramanujan: Modular equations and approximations to . In: Quarterly Journal of Mathematics. Band 45. 1914, S. 350–372, abgerufen am 5. März 2024.
- ↑ Jonathan Borwein, Peter Borwein, D. H. Bailey, S. Ramanujan: Modular equations and approximations to pi or how to compute one billion digits of pi. (PDF) In: American Mathematical Monthly. Band 96. 1989, S. 201–219, abgerufen am 5. März 2024.
- ↑ David H. Bailey, Jonathan M. Borwein: Pi: The next generation. Springer, Switzerland 2016, S. 175.
- ↑ Nayandeep Deka Baruah, Bruce C. Berndt, Heng Huat Chan: Ramanujan’s series for 1/π: a survey. In: American Mathematical Monthly. Band 116, Nr. 7, 2009, S. 567–587, doi:10.4169/193009709X458555, JSTOR:40391165. Abgerufen am 5. März 2024.
- ↑ J. Arndt, C. Haenel: Pi. Algorithmen, Computer, Arithmetik. 2. Auflage, Berlin/Heidelberg 2000, S. 19.
- ↑ Terence Tao: Analysis II. New Delhi 2006, S. 90.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 198–199.
- ↑ Peter Bundschuh: Einführung in die Zahlentheorie. 6. Auflage, Springer-Verlag, Berlin/Heidelberg 2008, S. 257.
- ↑ Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications.). Cambridge University Press, Cambridge / New York 2003, ISBN 0-521-81805-2, S. 2.
- ↑ Roger Apéry: Irrationalité de et . In: Astérisque. Band 61, 1979, S. 11–13.
- ↑ Weiping Wanga, Ce Xub: Alternating multiple zeta values, and explicit formulas of some Euler-Apéry-type series. (Volltext als PDF; 255 kB; abgerufen am 5. März 2024).
- ↑ Jakob Ablinger: Discovering and proving infinite binomial sums identities. In: Experimental Mathematics. Band 26, Nr. 1, 2017, S. 62–71 (doi:10.1080/10586458.2015.1116028).
- ↑ D. H. Bailey, J. M. Borwein, D. M. Bradley: Experimental determination of Apéry-like identities for ζ(2n + 2). In: Experimental mathematics. Band 15, Nr. 3, 2006, S. 281–289.
- ↑ Z.-W. Sun: A new series for and related congruences. In: International Journal of Mathematics. Band 26, Nr. 8, 2015, Artikel: 1550055.
- ↑ I. J. Zucker: On the series and related sums. In: Journal of Number Theory. Band 20, Nr. 1, 1985, S. 92–102.
- ↑ S. R. Finch: Mathematical Constants. Cambridge / New York 2003, S. 45.
- ↑ S. R. Finch: Mathematical Constants. Cambridge / New York 2003, S. 20.
- ↑ S. R. Finch: Mathematical Constants. Cambridge / New York 2003, S. 31.
- ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. Providence (RI) 2015, S. 3.
- ↑ Anil Nerode, Noam Greenberg: Algebraic Curves and Riemann Surfaces for Undergraduates. Switzerland 2022, S. 309.
- ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. Providence (RI) 2015, S. 4.
- ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. Providence (RI) 2015, S. 4–5.
- ↑ H. M. Edwards: Riemann’s Zeta Function. New York 1974, S. 104.
- ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. Providence (RI) 2015, S. 5.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part II. New York 1989, S. 220–221.
- ↑ E. Stein, R. Shakarchi: Complex analysis. Princeton (NJ) 2003, S. 154.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part II. New York 1989, S. 235.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 177.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer, Berlin/Heidelberg 1995, S. 117.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Berlin/Heidelberg 1995, S. 27.
- ↑ H. M. Edwards: Riemann’s Zeta Function. New York 1974, S. 218.
- ↑ Bruce C. Berndt: Ramanujan’s Notebooks Part II. New York 1989, S. 190.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 418–429.
- ↑ Olivier Ramaré: Excursions in Multiplicative Number Theory. Birkhäuser, Switzerland 2022, S. 60.
- ↑ S. Chowla: On some infinite series involving arithmetical functions. Proc. Indian Acad. Sci. 5, 511–513 (1937). https://doi.org/10.1007/BF03050153.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 253.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 255.
- ↑ Kathrin Bringmann, Chris Jennings-Shaffer, Karl Mahlburg: On a Tauberian theorem of Ingham and Euler–Maclaurin summation. In: The Ramanujan Journal. doi:10.1007/s11139-020-00377-5, 2021, S. 4–5.
- ↑ Kathrin Bringmann, Chris Jennings-Shaffer, Karl Mahlburg: On a Tauberian theorem of Ingham and Euler–Maclaurin summation. In: The Ramanujan Journal. doi:10.1007/s11139-020-00377-5, 2021, S. 5.
- ↑ Gérald Tenenbaum: Introduction to analytic and probabilistic number theory, AMS, 1990, S. 350
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 234.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage, Berlin 2006, S. 199–200.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage, Berlin u. a. 1996, S. 237.
- ↑ Achim Klenke: Wahrscheinlichkeitstheorie (= Springer-Lehrbuch Masterclass.). 3., überarbeitete und ergänzte Auflage, Springer Spektrum, Berlin/Heidelberg 2013, ISBN 978-3-642-36018-3, S. 332.
- ↑ Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage, Berlin/Heidelberg 2013, S. 111 ff.
- ↑ Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Berlin/Heidelberg 2013, S. 326.
- ↑ Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage, Berlin/Heidelberg 2013, S. 12.
- ↑ Herold Dehling, Beate Haupt: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 2. Auflage, Springer-Verlag Berlin Heidelberg 2004, ISBN 3-540-20380-X, S. 13.
- ↑ Emmanuel Kowalski: An Introduction to Probabilistic Number Theory. In: Cambridge studies in advanced mathematics. Band 192, S. 47 ff.
- ↑ a b Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 290.
- ↑ G. Tenenbaum: Introduction to Analytic and Probabilistic Number Theory. 3. Edition, Providence (RI) 2015, S. 317–348.
- ↑ Marius Overholt: A Course in Analytic Number Theory. Providence (RI) 2014, S. 157–162.
- ↑ Marius Overholt: A Course in Analytic Number Theory. Providence (RI) 2014, S. 111–150.
- ↑ George Andrews: The Theory of Partitions. Cambridge 1984, S. 71 ff.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume One: Arithmetic Equivalents. In: Encyclopedia of Mathematics and Its Applications. Band 164, S. 143.
- ↑ Dimitris Koukoulopoulos, James Maynard: On the Dufin-Shaeffer conjecture. In: Annals of Mathematics. Band 192, 2020, S. 251–307.
- ↑ Serge Lang: Undergraduate Analysis. 2. Edition, New York 1997, S. 216–217.
- ↑ Ben Green, Terence Tao: The primes contain arbitrarily long arithmetic progressions. In: Annals of Mathematics. Band 167. Jahrgang, Nr. 2, 2008, S. 481–547.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1995, S. 36.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory. From Euclid to Hardy and Littlewood. Berlin/Heidelberg 2000, S. 51.




























































































































































![{\displaystyle R[[z]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70ecc69b6832ae7e87f86a044c44cd5f31b3f7e0)

![{\displaystyle \mathbb {C} [[z]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8c0bdf919d9e2cc4236027eb44fd8af8a9986ea)












































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle \int _{t_{0}}^{t}\sum _{n=1}^{\infty }f_{n}(x)\mathrm {d} x=\sum _{n=1}^{\infty }\int _{t_{0}}^{t}f_{n}(x)\mathrm {d} x,\qquad t_{0},t\in [a,b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d1dc3349b892256af8b022bc7078ab840c4172a)
![{\displaystyle \left(\sum _{n=1}^{\infty }f_{n}(x)\right)'=\sum _{n=1}^{\infty }f_{n}'(x),\qquad x\in [a,b].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab5273dfa55d822522b212da248dd7c6a25e738d)















































































![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
































![{\displaystyle \pi \cot(\pi z)={\frac {1}{z}}+\sum _{n=1}^{\infty }\left[{\frac {1}{z+n}}+{\frac {1}{z-n}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/494204722b5cea3e57aa5d6c8ff9df87269f681f)







































![{\displaystyle \textstyle \alpha :=\limsup _{n\to \infty }{\sqrt[{n}]{|a_{n}|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05d941bf161307490fff992f798febcbed8a8811)



![{\displaystyle {\sqrt[{n}]{|a_{n}|}}\leq q<1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3458cce95a34e914f26177742e0a0554358e4492)








































































































































































































![{\displaystyle n\cdot {\sqrt[{n}]{a_{1}a_{2}\cdots a_{n}}}\leq \sum _{k=1}^{n}a_{k}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09b6645ea109d8cd11787abf95e45bcd01c305a9)




























![{\displaystyle [m,M]\subset I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a279b8d4822408cdfa0d9c0a977ba0a02c2e0a6b)
![{\displaystyle (x_{1},\dotsc ,x_{n})\in [m,M]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b640e837fbfa9fbe4a2277cf687588b753c7dce3)


















































![{\displaystyle f\colon [0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/972965f41326a60c0c47be81b271ffbc231e180e)





















![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
































































































![{\displaystyle [1,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63470e8fe9faf7ae30b257d12486bf1730330e5f)




![{\displaystyle [M,N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c832e715f4f08b52d437084d83a303a9a6aa3d3f)

![{\displaystyle \vartheta =\vartheta (M,N)\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/073cc1f1ad33208b52692efcab76bfec8c96182d)








![{\displaystyle \vartheta _{n}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/152d8c4ac2bd54256ff821e38f89e4b2d1428b7a)












































![{\displaystyle g\colon [a,b]\to [0,\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/150cd60d772db41f6d7237129f71951459c3d0e7)















![{\displaystyle \int _{0}^{\infty }x^{s-1}\left[\phi (0)-\phi (1)x+\phi (2)x^{2}-\cdots \right]\mathrm {d} x={\frac {\pi }{\sin(\pi s)}}\phi (-s).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e9a703c039b0d4a00dd3dcb8c2136a052071a0c)
![{\displaystyle \int _{0}^{\infty }x^{-s}\left[\phi (1)-\phi (2)x+\phi (3){\frac {x^{2}}{2!}}-\phi (4){\frac {x^{3}}{3!}}+\cdots \right]\mathrm {d} x=\Gamma (1-s)\phi (s).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf09e7b32aaeab3935fdb877454be5ac161454fd)



































































































![{\displaystyle \alpha \in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daf3c62599ea71319c85f715c9e590d2bab2d036)
















