Cauchy-Kriterium

Das (Bolzano-)Cauchy-Kriterium (auch: Konvergenzprinzip, [allgemeines] Kriterium von Bolzano-Cauchy oder Konvergenzkriterium von Bolzano-Cauchy) ist ein mathematisches Konvergenzkriterium für Folgen und Reihen und von grundlegender Bedeutung für die Analysis. Mit ihm kann auch ohne Kenntnis des Grenzwerts entschieden werden, ob eine Folge oder Reihe reeller oder komplexer Zahlen konvergent oder divergent ist. Allgemeiner kann das Cauchy-Kriterium auch auf Folgen von Elementen eines vollständigen metrischen Raums oder auf Reihen von Vektoren eines Banachraums angewandt werden. Es handelt sich bis heute um eines der wenigen Kriterien, die eine hinreichende und notwendige Bedingung für die Konvergenz von Reihen angeben. Das Cauchy-Kriterium ist nach dem französischen Mathematiker Augustin Louis Cauchy benannt, der es 1821 in seinem Lehrbuch Cours d’Analyse veröffentlichte.

Eine Folge konvergiert, wenn der Abstand der Folgenglieder im Verlauf der Folge beliebig klein wird.

Wenn der Abstand der Folgenglieder im Verlauf der Folge nicht beliebig klein wird, dann divergiert die Folge.

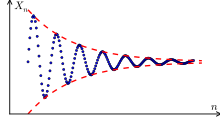
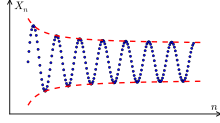
Cauchy-Kriterium für Folgen

Kriterium

Eine Folge $(a_{n})_{n\in \mathbb {N} }=a_{1},a_{2},\ldots$ reeller oder komplexer Zahlen konvergiert genau dann gegen einen reellen bzw. komplexen Grenzwert, wenn sie die folgende Eigenschaft hat: Zu jedem $\varepsilon >0$ gibt es einen Index $N$ gibt, sodass der Abstand zweier beliebiger Folgenglieder ab diesem Index kleiner als $\varepsilon$ ist.

Diese Eigenschaft wird in der Literatur auch als Cauchy-Bedingung bezeichnet. Formal liest sie sich als

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad \left|a_{m}-a_{n}\right|<\varepsilon$.

Eine Folge, welche die Cauchy-Bedingung erfüllt, ist eine Cauchy-Folge. Das Kriterium lässt sich somit prägnant fomulieren durch:

Eine Folge reeller oder komplexer Zahlen konvergiert genau dann, wenn sie eine Cauchy-Folge ist.

Das Beispiel ${\textstyle a_{n}=\sum _{k=1}^{n}{\frac {1}{k}}}$ (Harmonische Reihe) zeigt, dass es im Cauchy-Kriterium wirklich auf den Abstand zweier beliebiger Folgenglieder ab dem Index $N$ ankommt und nicht nur auf den Abstand aufeinanderfolgender Folgenglieder.

Beispiel

Die Folge reeller Zahlen $(a_{n})$ sei rekursiv durch

$a_{n+1}={\tfrac {1}{2}}(1-a_{n}^{2})$

gegeben, wobei $a_{0}=0$ ist. Um die Konvergenz dieser Folge mit dem Cauchy-Kriterium zu zeigen, berechnet man zunächst

$|a_{n+1}-a_{n}|=|{\tfrac {1}{2}}(1-a_{n}^{2})-{\tfrac {1}{2}}(1-a_{n-1}^{2})|={\tfrac {1}{2}}|a_{n}^{2}-a_{n-1}^{2}|={\tfrac {1}{2}}|a_{n}+a_{n-1}|\,|a_{n}-a_{n-1}|\leq {\tfrac {1}{2}}|a_{n}-a_{n-1}|$,

wobei die letzte Abschätzung aus der Dreiecksungleichung

$|a_{n}+a_{n-1}|\leq |a_{n}|+|a_{n-1}|\leq 1$

folgt, da die einzelnen Folgenglieder durch ${\tfrac {1}{2}}$ beschränkt sind. Wendet man die Ungleichung $n$-mal an, erhält man mit $q={\tfrac {1}{2}}$

$|a_{n+1}-a_{n}|\leq q^{n}|a_{1}-a_{0}|=q^{n+1}$.

Allgemein gilt nun für $m>n$

$|a_{m}-a_{m-1}|\leq q|a_{m-1}-a_{m-2}|\leq \cdots \leq q^{m-n-1}|a_{n+1}-a_{n}|$

und durch wiederholte Anwendung der Dreiecksungleichung sowie der geometrischen Summenformel

$|a_{m}-a_{n}|\leq \sum _{i=0}^{m-n-1}q^{i}|a_{n+1}-a_{n}|\leq {\frac {1-q^{m-n}}{1-q}}q^{n+1}\leq {\frac {1}{1-q}}q^{n+1}=2q^{n+1}=q^{n}<\varepsilon$

für alle $n,m>N={\tfrac {\ln \varepsilon }{\ln q}}$. Damit ist die Folge $(a_{n})$ eine Cauchy-Folge und somit konvergent.

Cauchy-Kriterium und Vollständigkeit

Es besteht ein enger Zusammenhang zwischen dem Cauchy-Kriterium und der Vollständigkeit der reellen und komplexen Zahlen. Ein metrischer Raum ist per Definition vollständig, wenn jede Cauchy-Folge von Elementen des Raums in ihm konvergiert. Demzufolge besagt der „Dann-Teil“ des Cauchy-Kriteriums, dass die reellen bzw. komplexen Zahlen vollständig sind. Das Cauchy-Kriterium kann somit als Vollständigkeitsaxiom für die reellen oder komplexen Zahlen herangezogen werden.

Beweis

Ist $\left(a_{n}\right)$ eine konvergente Folge mit Grenzwert $a$, so muss für beliebig kleines $\varepsilon >0$ nach der Definition der Konvergenz ${\textstyle |a-a_{n}|<{\frac {\varepsilon }{2}}}$ und ${\textstyle |a-a_{m}|<{\frac {\varepsilon }{2}}}$ für hinreichend große $n$ und $m$ sein. Mit der Dreiecksungleichung folgt hieraus $|a_{n}-a_{m}|=|(a-a_{m})-(a-a_{n})|\leq |a-a_{m}|+|a-a_{n}|<\varepsilon .$ Also ist die Cauchy-Bedingung erfüllt.

Der Beweis der Rückrichtung hängt von der Wahl des Vollständigkeitsaxioms ab. Wird das Cauchy-Kriterium selbst als Vollständigkeitsaxiom gesetzt, so muss nichts gezeigt werden. Wird der Satz von Bolzano-Weierstraß als Vollständigkeitsaxiom zugrunde gelegt und ist $(a_{n})$ eine Cauchy-Folge, dann kann man zu $\varepsilon =1$ einen Index $N\in \mathbb {N}$ finden, sodass

$|a_{n}|=|a_{n}-a_{N}+a_{N}|\leq |a_{n}-a_{N}|+|a_{N}|\leq 1+|a_{N}|$

für alle $n\geq N$ ist. Also ist die Cauchy-Folge durch

$\max\{|a_{1}|,|a_{2}|,\ldots ,|a_{N-1}|,1+|a_{N}|\}$

beschränkt. Der Satz von Bolzano-Weierstraß besagt nun, dass die Folge $(a_{n})$ einen Häufungspunkt $a$ besitzt. Bezeichnet $(a_{n_{i}})_{i\in \mathbb {N} }$ eine Teilfolge, die gegen $a$ konvergiert, ergibt sich mit

$|a_{n}-a|\leq |a_{n}-a_{n_{i}}|+|a_{n_{i}}-a|$,

dass $a$ der Grenzwert der gesamten Folge sein muss.

Verallgemeinerung

Allgemeiner kann das Cauchy-Kriterium auch zur Untersuchung der Konvergenz von Folgen von Elementen eines vollständigen metrischen Raums $(X,d)$ verwendet werden. Eine Folge $(x_{n})_{n\in \mathbb {N} }$ von Elementen $x_{n}\in X$ konvergiert genau dann gegen einen Grenzwert in der Menge $X$, wenn sie eine Cauchy-Folge bezüglich der Metrik $d$ ist, wenn also gilt:

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad d(x_{m},x_{n})<\varepsilon$.

In einem nicht vollständigen metrischen Raum bildet die Cauchy-Bedingung nur eine notwendige Bedingung für die Konvergenz einer Folge, das heißt: ist eine gegebene Folge keine Cauchy-Folge, so divergiert sie.

Cauchy-Kriterium für Reihen

Kriterium

Eine Reihe ${\textstyle \sum _{k=1}^{\infty }a_{k}=a_{1}+a_{2}+\ldots }$ mit reellen oder komplexen Summanden $a_{k}$ konvergiert genau dann, wenn folgende Bedingung erfüllt ist: Zu jedem $\varepsilon >0$ gibt es einen Index $N$ gibt, so dass jede Summe, die aus (beliebig vielen) Folgengliedern ab diesem Index gebildet wird, vom Betrag her kleiner als $\varepsilon$ ist. Formel liest sich diese Bedingung als

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m>n\geq N\colon \quad |a_{n+1}+a_{n+2}+\ldots +a_{m}|<\varepsilon .$

Beispiele

Die Reihe $1+{\tfrac {1}{4}}+{\tfrac {1}{9}}+{\tfrac {1}{16}}+\ldots$ konvergiert, da für $N>{\tfrac {1}{\varepsilon }}$ gilt:

$\left|\sum _{k=n+1}^{m}{\frac {1}{k^{2}}}\right|<\left|\sum _{k=n+1}^{m}{\frac {1}{k(k-1)}}\right|=\left|\sum _{k=n+1}^{m}\left({\frac {1}{k-1}}-{\frac {1}{k}}\right)\right|={\frac {1}{n}}-{\frac {1}{m}}<{\frac {1}{n}}\leq {\frac {1}{N}}<\varepsilon$.

Hingegen divergiert die harmonische Reihe $1+{\tfrac {1}{2}}+{\tfrac {1}{3}}+{\tfrac {1}{4}}+\ldots$, denn wählt man $\varepsilon ={\tfrac {1}{2}}$, $N$ beliebig, $n\geq N$ und $m=2n$, so gilt immer

$\left|\sum _{k=n+1}^{m}{\frac {1}{k}}\right|=\left|{\frac {1}{n+1}}+\ldots +{\frac {1}{2n}}\right|\geq n\cdot {\frac {1}{2n}}={\frac {1}{2}}\geq \varepsilon$.

Beweis

Das Cauchy-Kriterium für Reihen folgt aus dem Cauchy-Kriterium für Folgen: Man wendet das Cauchy-Kriterium für Folgen auf die Folge $(s_{n})$ der Partialsummen an und benutzt den Zusammenhang

$|s_{m}-s_{n}|=|(a_{1}+\ldots +a_{m})-(a_{1}+\ldots +a_{n})|=|a_{n+1}+\ldots +a_{m}|$.

Verallgemeinerung

Allgemeiner lässt sich das Cauchy-Kriterium auch für Reihen von Vektoren aus einem vollständigen normierten Raum $(V,\|\cdot \|)$ fassen:

Eine Reihe ${\textstyle \sum _{k=1}^{\infty }v_{k}}$ von Vektoren $v_{k}\in V$ konvergiert genau dann gegen einen Grenzwert in $V$, wenn gilt:

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m>n\geq N\colon \quad \|v_{n+1}+v_{n+2}+\ldots +v_{m}\|<\varepsilon$.

Siehe auch

• Monotoniekriterium

Literatur

• Konrad Königsberger: Analysis 1. Springer-Verlag, Berlin u. a. 2004, ISBN 3-540-41282-4.
• Otto Forster: Analysis Band 1: Differential- und Integralrechnung einer Veränderlichen. 8. Auflage. Vieweg-Verlag, 2006, ISBN 3-528-67224-2.
• Richard Courant: Vorlesungen über Differential- und Integralrechnung 1. 4. Aufl., Springer, Berlin / Heidelberg 1971, ISBN 3-540-05466-9.

Weblinks

Wikibooks: Mathe für Nicht-Freaks: Cauchy-Folgen und das Cauchy-Kriterium – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Cauchy-Kriterium für Reihen – Lern- und Lehrmaterialien

• L.D. Kudryavtsev: Cauchy criteria. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org). 
• Cauchy Criterion for Convergence. In: PlanetMath. (englisch)
• Eric W. Weisstein: Cauchy Criterion. In: MathWorld (englisch).