Riemannsche Vermutung

Die Riemannsche Vermutung, Riemannsche Hypothese, Riemannhypothese oder kurz RH trifft eine Aussage über die Verteilung der Primzahlen und ist nach Meinung führender Mathematiker das derzeit bedeutendste ungelöste Problem der reinen Mathematik. Sie wurde erstmals 1859 von Bernhard Riemann in seiner Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe in einem Nebensatz formuliert. Nachdem sie bereits im Jahr 1900 von David Hilbert auf seine Liste 23 wichtiger Jahrhundertprobleme gesetzt worden war, wurde sie im Jahr 2000 vom Clay Mathematics Institute in die Liste der sieben Millennium-Probleme der Mathematik aufgenommen. Das Institut in Cambridge (Massachusetts) hat damit ein Preisgeld von einer Million US-Dollar für eine schlüssige Lösung des Problems in Form eines mathematischen Beweises ausgelobt. Hinsichtlich des Auffindens potenzieller Gegenbeispiele existieren in der Preisausschreibung jedoch Sonderregeln, insbesondere dann, wenn diese mit der Rechenkraft moderner Computer erlangt wurden, und keinerlei „tiefere Einsicht“ in das Problem geben können.
Einfach gesprochen sagt die Riemannsche Vermutung aus, dass sich die Folge der Primzahlen „möglichst zufällig“ verhält. Das sollte sich zum Beispiel dadurch äußern, dass die Abfolge der Ereignisse, dass eine Zahl eine gerade Anzahl an Primfaktoren besitzt, wie zum Beispiel , oder eine ungerade Anzahl an Primfaktoren besitzt, wie , für , also nach dem Schema (mit Null Primfaktoren für die 1)
auf lange Sicht ungefähr ein Verhalten aufweist, das auch ein unendlich häufig wiederholter Münzwurf mit „Kopf“ und „Zahl“ realistischerweise haben könnte. Eine Theorie, welche die Riemannsche Vermutung löst und damit eine tiefere Erklärung für diese Zufälligkeit unter den Primzahlen lieferte, könnte daher aus Sicht der Mathematiker ein fundamental neues Verständnis für Zahlen im Allgemeinen nach sich ziehen.
Übersetzt man dies in die Fachsprache der analytischen Zahlentheorie, ist die Riemannsche Vermutung gleichbedeutend mit der Aussage, dass sämtliche komplexe Nullstellen der Riemannschen Zeta-Funktion im sog. kritischen Streifen den Realteil besitzen. Dies ist auch die ursprünglich von Riemann formulierte Version der Vermutung. Die Zeta-Funktion ist eine mathematische Funktion, die Informationen über Primzahlen in ihrem Abbildungsverhalten kodiert: Bereits Leonhard Euler erkannte, dass sie sich als ein Euler-Produkt über die Primzahlen darstellen lässt, sich die Funktionswerte also mit Hilfe der Primzahlen bestimmen lassen. Auf der anderen Seite kann die Zeta-Funktion als ein Produkt über ihre Nullstellen dargestellt werden, ähnlich wie sich Polynome durch ihre Nullstellen faktorisieren lassen, wie etwa . Es liegen also zwei verschiedene Produktdarstellungen derselben Funktion vor. Durch dieses hiervon induzierte Zusammenspiel ergibt sich, dass die Nullstellen Eigenschaften der Primzahlen kodieren, und die Primzahlen wiederum Eigenschaften der Nullstellen. Mathematiker sprechen in diesem Zusammenhang oft von einer „Dualität“.
Es ist schon bekannt und bewiesen, dass die Zeta-Funktion reelle Nullstellen hat, die sogenannten trivialen Nullstellen. Ferner weiß man seit Beginn des 20. Jahrhunderts, dass die Zeta-Funktion unendlich viele nichtreelle Nullstellen mit dem Realteil besitzt. Die Riemannsche Vermutung besagt also, dass es darüber hinaus keine weiteren Nullstellen gibt, d. h., dass alle nichttrivialen Nullstellen der Zeta-Funktion auf einer Geraden in der Zahlenebene parallel zur imaginären Achse liegen. Da die Zeta-Funktion über eine Funktionalgleichung ein elementares Spiegelungsgesetz bezüglich besitzt, ist sie äquivalent dazu, dass sich sämtliche Nullstellen „möglichst weit links“ befinden, wobei „linke Nullstellen“ eine eher gleichmäßige Primzahlverteilung zur Folge haben. Gleichzeitig baut die bloße Existenz von diesen Nullstellen eine natürliche Barriere auf, die so gedeutet werden kann, dass Primzahlen nicht beliebig gleichmäßig, wie etwa „Kopf, Zahl, Kopf, Zahl, Kopf, Zahl, …“, verteilt sein können.
Viele bisher ungelöste Fragestellungen, besonders aus der Zahlentheorie, können mit der Richtigkeit der Riemannschen Vermutung beantwortet werden. Dies betrifft Probleme aus der mathematischen Grundlagenforschung, wie etwa solche der Primzahlverteilung im Umfeld des Primzahlsatzes oder der offenen Goldbachschen Vermutung, als auch der angewandten Mathematik, wie schnelle Primzahltests. Gleichzeitig gilt sie auch als äußerst schwierig zu beweisen. Bisherige Beweisversuche von prominenten Mathematikern scheiterten allesamt. Ein Grund hierfür ist, dass die Menschheit aus Expertensicht bisher nicht über die nötigen mathematischen Werkzeuge verfügt, sie überhaupt angreifen zu können. So gilt es als sehr wahrscheinlich, dass sie nicht mit rein analytischen Mitteln, also durch bloße Untersuchung des „Funktionsterms“ der Zeta-Funktion mittels des Theorieapparats der holomorphen Funktionen, gezeigt werden kann, sondern mit dem Euler-Produkt eine entscheidende arithmetische Komponente mitspielen muss, obwohl dieses im kritischen Streifen nicht mehr konvergiert, was erhebliche Schwierigkeiten mit sich bringt. So gibt es andere Zeta-Funktionen, die der Riemannschen Zeta-Funktion in ihren Eigenschaften sehr stark ähneln, jedoch kein Euler-Produkt besitzen, und bei denen die Riemannsche Vermutung erwiesenermaßen falsch ist.
Durch umfassenden Einsatz von Computern ist es gelungen, die Riemannsche Vermutung für die ersten 10 Billionen Nullstellen der Zeta-Funktion zu bestätigen. Da die Zeta-Funktion jedoch nachweislich unendlich viele nichtreelle Nullstellen besitzt, könnte sie auf diese Weise nur durch Angabe eines expliziten Gegenbeispiels widerlegt, jedoch nicht bewiesen werden. Ein Gegenbeispiel wäre eine Nullstelle im kritischen Streifen mit Realteil ungleich .
Überblick Bearbeiten



Im Zentrum der Zahlentheorie, jenes Zweiges der Mathematik, der sich mit den Eigenschaften der natürlichen Zahlen 1, 2, 3, 4, … beschäftigt, stehen die Primzahlen 2, 3, 5, 7, 11, … Diese sind ausgezeichnet durch die Eigenschaft, genau zwei Teiler zu haben, nämlich die 1 und sich selbst. Die 1 ist keine Primzahl. Primzahlen bilden gewissermaßen die Atome der ganzen Zahlen, da sich jede positive ganze Zahl eindeutig multiplikativ in solche zerlegen lässt. Dieses Resultat wird auch als Fundamentalsatz der Arithmetik bezeichnet. Zum Beispiel gilt 21 = 3 · 7 und 110 = 2 · 5 · 11.
Trotz ihrer einfachen Definition ist nach mehreren Jahrtausenden Mathematikgeschichte bis heute kein Muster bekannt, dem sich die Primzahlen in ihrer Folge unterwerfen. Ihre Natur ist eine der bedeutendsten offenen Fragen der Mathematik. Die Riemannsche Vermutung ist eine bis heute nicht bewiesene Aussage über die Verteilung der Primzahlen und motiviert sich aus folgenden Fragestellungen:[1]
- Wie viele Primzahlen 2, 3, 5, 7, 11, … gibt es unter der Zahl 100? Und wie viele sind es unterhalb 10 000 oder 1 000 000?
- Allgemeiner, wie viele Primzahlen gibt es unterhalb einer beliebigen Zahl, etwa X?
Auf den ersten Blick sind dies Fragen sehr spezieller Natur, lediglich die Theorie der Zahlen, bzw. Primzahlen, betreffend. Mathematiker, und später auch Physiker, haben jedoch herausgefunden, dass sie mit einer Vielzahl von Strukturen zusammenhängen, die zahlreiche Felder der mathematischen Wissenschaften verknüpfen. Dies betrifft etwa die Quantenphysik, aber auch die Wahrscheinlichkeitstheorie, jener Zweig der Mathematik, der sich mit dem Zufall befasst. All diese Zusammenhänge sind bisher weder exakt formalisiert, noch verstanden worden. Sie alle münden jedoch gemeinsam in der Riemannschen Vermutung: Die Primzahlen stehen in einer Dualität[2][3][4] zu einem anderen Typ mathematischer Objekte. Dabei bedeutet Dualität, dass es eine natürliche Paarung zwischen den Primzahlen und diesen anderen Objekten gibt. In etwa übertragen sich Informationen über die Primzahlen zu diesen anderen Objekten, aber auch vice versa kodieren Primzahlen Informationen über ihre „Partnerobjekte“. Bei diesen Objekten handelt es sich wieder um Zahlen. Diese unterteilen sich in zwei Kategorien:
- Bereits Mitte des 19. Jahrhunderts erkannte Bernhard Riemann, dass die negativen geraden Zahlen, also , ein Teil dieser Dualität sind. Man bezeichnet diesen Teil bis heute auch als trivial, da die mathematische Tiefe für dessen Verständnis nicht so hoch ist.
- Die übrigen, nichttrivialen „Dualzahlen“ treten nicht als „Zählzahlen“ in Erscheinung, wie es etwa die Primzahlen 2 und 3 auf der anderen Seite der Dualität noch taten, sondern es handelt sich um bestimmte komplexe Zahlen.
Im Kontrast zu der „völlig willkürlichen Anordnung“ der Primzahlen scheint den nichttrivialen „Dualzahlen“ ein sehr strenges Muster zu Grunde zu liegen: wie alle komplexen Zahlen können sie zunächst auf einer Ebene visualisiert werden, und die Riemannsche Vermutung sagt aus, dass die zu den Primzahlen gehörigen nichttrivialen „Dualzahlen“ innerhalb der Ebene alle auf einer gemeinsamen Geraden platziert sind. Sie tragen demnach vermutlich eine starke geometrische Symmetrie.
Die Gründe, weshalb ein Beweis der Riemannschen Vermutung bahnbrechend für die Mathematik wäre, sind vielseitig: Die geometrische Lage der nichttrivialen „Dualzahlen“ birgt Informationen zu der Verteilung der Primzahlen. Kennt man alle Dualzahlen, so kann damit sogar die exakte Verteilung der Primzahlen rechnerisch beliebig genau rekonstruiert werden (siehe unteres Bild zur Primzahlhäufigkeit). Durch das Dualitätsprinzip gehen also wechselseitig keine Informationen verloren. In theoretischer Hinsicht ließe sich die Lage auf einer gemeinsamen Geraden dadurch interpretieren, dass die Primzahlen möglichst gleichmäßig und damit pseudozufällig verteilt sind. Sie liegen also „alle bereits fest“, jedoch ist es schwierig, dem Verteilungsmuster einfache Notwendigkeiten abzuringen. Zum Beispiel kann in den Primfaktorzerlegungen benachbarter Zahlen, wie etwa
bislang kein notwendiger Zusammenhang erkannt werden. Viele bisher nicht bewiesene Vermutungen der Zahlentheorie würden zudem aus dem Beweis der Riemannhypothese als „Zugabe“ direkt mit folgen. Dazu zählen auch verbesserte Primzahltests, die in der Kryptographie praktische Anwendungen finden.[5] Die Theorie der Riemannschen Vermutung führt darüber hinaus viele Gebiete der Mathematik zusammen. Tut dies eine Theorie, spricht dies für eine Form der Fundamentalität. Beispiel einer solchen fundamentalen Theorie ist der Ende des 20. Jahrhunderts bewiesene Modularitätssatz, der mit elliptische Kurven und Modulformen zwei auf den ersten Blick völlig verschiedene Theorien zusammenbrachte. Ein tieferes Verständnis der Primzahlen könnte auch neue Entwicklungen in der Quantenphysik nach sich ziehen. Wäre die Symmetrie unter den „Dualzahlen“ erfüllt, könnte dieses System zum Beispiel möglicherweise als Quasikristall aufgefasst werden.
Das Phänomen der Dualität lässt sich anhand einer berühmten anderen Zahlenfolge veranschaulichen, der Fibonacci-Folge
Die Folge beginnt per Definition mit 0 und 1, und die Summe der beiden vorherigen Zahlen ergibt stets die folgende Zahl. In der Mathematik bezeichnet man solche Folgen auch als rekursiv. Die Fibonacci-Folge lässt sich damit implizit durch
- und mit
definieren. Die Relation schlägt eine Brücke in die Algebra, wo sie in der Gleichung Ausdruck findet.[Anm. 1] Diese quadratische Gleichung kann durch die Mitternachtsformel gelöst werden, wobei man die Lösungen und erhält. Es ist dabei der negative goldene Schnitt, und dieser wie auch stehen in Dualität zur Fibonacci-Folge. Aus beiden Nullstellen rekonstruiert sich jeder Fibonacci-Wert über die exakte Formel
und aus der Fibonacci-Folge lässt sich andersherum der goldene Schnitt konstruieren durch . Die endliche Rekursion hinter den Fibonacci-Zahlen garantiert eine geringe mathematische Komplexität dieser Folge, und entsprechend „klein“ ist die Menge der „Dualzahlen“ . Die Primzahlen hingegen erfüllen keine endliche Rekursion, und ihre „genaue Zusammensetzung“ ist sehr kompliziert. Auch sie können, unter Ausnutzung der eindeutigen Primfaktorzerlegung natürlicher Zahlen, in einer Funktion kodiert werden. Bei diesem Prozess nimmt die charakteristische Eigenschaft der Primzahlen, die natürlichen Zahlen multiplikativ aufzubauen, eine analoge Rolle ein wie bei der Assoziation der Fibonacci-Folge mit der Funktion . Die durch die Primzahlen gewonnene Funktion ist jedoch um einiges komplizierter als die quadratische Funktion . Man bezeichnet sie als Riemannsche Zeta-Funktion, und ihre Nullstellen sind die zu den Primzahlen gehörigen „Dualzahlen“. Die Zeta-Funktion ist, im Gegensatz zu , keine rationale Funktion, kann also nicht durch eine endliche Abfolge der vier Grundrechenarten (Plus, Minus, Mal und Geteilt) aus dem Eingabewert berechnet werden. Sie hat unendlich viele Nullstellen, und die hohe Komplexität der Primzahlen drückt sich dadurch aus, dass folglich die Menge der „Dualzahlen“ unendlich groß ist.
Der Zahlentheoretiker Don Zagier fasste das Problem auf seiner am 5. Mai 1975 gehaltenen Antrittsvorlesung an der Universität Bonn wie folgt zusammen:
„Es gibt zwei Tatsachen über die Verteilung von Primzahlen […]: Die eine ist, daß die Primzahlen, trotz ihrer einfachen Definition und Rolle als Bausteine der natürlichen Zahlen, zu den willkürlichsten, widerspenstigsten Objekten gehören, die der Mathematiker überhaupt studiert. Sie wachsen wie Unkraut unter den natürlichen Zahlen, scheinbar keinem anderen Gesetz als dem Zufall unterworfen, und kein Mensch kann voraussagen, wo wieder eine sprießen wird, noch einer Zahl ansehen, ob sie prim ist oder nicht. Die andere Tatsache ist viel verblüffender, denn sie sagt just das Gegenteil, daß die Primzahlen die ungeheuerste Regelmäßigkeit aufzeigen, dass sie durchaus Gesetzen unterworfen sind und diesen mit fast peinlicher Genauigkeit gehorchen.“
Notation Bearbeiten
Es werden durchweg folgende Bezeichnungen verwendet:
- , , , und bezeichnen die natürlichen, ganzen, rationalen, reellen bzw. komplexen Zahlen.
- Die Notation für asymptotische Beschränktheit durch Landau-Symbole: Es bedeutet , dass (wobei meist ). Analog wird mit gebraucht, und mögliche Abhängigkeiten der absoluten Konstanten werden durch Eintragungen im Index gekennzeichnet. In etwa ist für alle . Ferner bedeutet sogar . Es bezeichnet hierbei den Limes superior.
- Es bezeichnen durchgängig und den Real- bzw. Imaginärteil der komplexen Zahl .
- Wie üblich ist durchgängig der natürliche Logarithmus von , und bzw. die natürliche Exponentialfunktion. Es bezeichnen den Integrallogarithmus und die Primzahl zählende Funktion.
- Es bezeichnet die Riemannsche Zeta-Funktion und die Gammafunktion. Zudem wird mit reellen und geschrieben.
- Es bezeichnen die Liouville-Funktion, die Möbius-Funktion und die Mangoldt-Funktion.
Bekannte Konzepte der Primzahlverteilung Bearbeiten
Die Unendlichkeit der Primzahlen Bearbeiten

Bereits Euklid konnte zeigen, dass es unendlich viele Primzahlen gibt, weshalb die Liste 2, 3, 5, 7, 11, … aller Primzahlen niemals endet, genauso wie die Liste 1, 2, 3, 4, … aller natürlichen Zahlen niemals endet. Sein Resultat wird als Satz des Euklid bezeichnet.[7]
Der Satz des Euklid ist ein mathematischer Satz; seine Richtigkeit muss daher bewiesen werden. Ein mathematischer Beweis erfolgt durch eine Aneinanderreihung logisch wahrer Argumente, die auf Axiomen oder bereits bewiesenen Sätzen aufbauen. Ein Beweis der Unendlichkeit der Primzahlen kann in etwa so geführt werden:
- Ist eine endliche Anzahl verschiedener Primzahlen gefunden, so bilde man deren Produkt. Anschließend addiere man das Ergebnis mit 1. Die dadurch entstandene Zahl ist nach Konstruktion durch keine Primzahl in der Liste teilbar. Da aber jede Zahl durch eine Primzahl teilbar ist, gibt es neben allen Primzahlen in der Liste eine weitere Primzahl.
Nachvollziehen lässt sich das Verfahren an folgendem Beispiel: Betrachtet man die Liste {2, 5, 11} von Primzahlen, so ist deren Produkt 2 · 5 · 11 = 110 durch 2, 5 und 11 teilbar. Damit kann 110 + 1 = 111 weder durch 2, 5 noch 11 teilbar sein, also gibt es eine weitere Primzahl, die sich von 2, 5 und 11 unterscheidet. In etwa teilt die Primzahl 3 die Zahl 111, und es gilt 111 = 3 · 37. Selbstverständlich ist die Listenlänge von drei Zahlen in diesem Beispiel willkürlich; man hat zum Beispiel
- 2 · 3 · 5 · 7 · 11 · 13 + 1 = 59 · 509,
und weder die Primzahlen 59 noch 509 sind in der Liste {2, 3, 5, 7, 11, 13} enthalten. Das Argument zeigt also, dass jede noch so lange Liste von Primzahlen unvollständig ist. Damit muss es unendlich viele Primzahlen geben.
Die Riemannsche Vermutung gibt eine quantitative Vorstellung von der Verteilung der Primzahlen, die über das bloße Wissen um deren Unendlichkeit sehr weit hinausgeht.
Eine Entdeckung Eulers Bearbeiten

Im Laufe der Zeit wurden zahlreiche Beweise für die Unendlichkeit der Primzahlen gefunden, darunter von Christian Goldbach, Leonhard Euler und Paul Erdös. Besonders Eulers Entdeckungen waren ein Wegweiser für die kommende Entwicklung von einer elementaren, in der Tradition der alten Griechen stehenden, hin zu einer modernen Form der Zahlentheorie. Im Jahr 1737, während seiner ersten Zeit in Sankt Petersburg, untersuchte Euler einen neuartigen Zugang zu den Primzahlen und fand heraus, dass sie „verhältnismäßig dicht“ unter den natürlichen Zahlen verstreut sind. Genauer bewies er
Summiert man also nacheinander die Kehrwerte der Primzahlen zusammen, wird auf Dauer jede noch so große obere Schranke durchbrochen. Dies zeigt auf, dass Primzahlen „dichter“ unter den natürlichen Zahlen verstreut sind als die Quadratzahlen,[8] denn Euler zeigte ebenfalls
Quadratzahlen wachsen also langfristig schnell genug an, dass die Summe ihrer Kehrwerte den endlichen Wert 1,645 nicht überschreitet. Euler stand seinerzeit nicht die mathematische Sprache zur Verfügung, diese Verschärfung des Euklidischen Satzes präzise zu interpretieren, und es gibt keinen Nachweis, dass er sich mit exakten Aussagen zur Verteilung von Primzahlen beschäftigte.[9] Allerdings hatte Euler bereits 1737 korrekterweise ohne Beweis behauptet, dass das Verhältnis , wobei die Anzahl der Primzahlen kleiner als bezeichnet, für wachsende gegen 0 strebt.[10]
Eulers Beweisstrategie nutzt das sog. Euler-Produkt. Dabei spielt die eindeutige Zerlegbarkeit natürlicher Zahlen in Primfaktoren eine Schlüsselrolle. Das Euler-Produkt steht in Zusammenhang zu einem Objekt, das bis heute in der Primzahlforschung benutzt wird und in der modernen Mathematik als Riemannsche Zeta-Funktion bekannt ist. Die Zeta-Funktion spielt ebenfalls für die Riemannsche Vermutung eine zentrale Rolle. Die neuartige Leistung bestand darin, Fragen zu Primzahlen systematisch durch funktionale Zusammenhänge zwischen Zahlen zu attackieren. Euler gilt deswegen als Initiator der analytischen Zahlentheorie.[11]
Der Primzahlsatz Bearbeiten
Die bloße Unendlichkeit einer Teilmenge der natürlichen Zahlen sagt noch nicht allzu viel über deren Natur aus. Zum Beispiel gibt es unendlich viele gerade Zahlen 2, 4, 6, 8, … und unendlich viele Quadratzahlen 1, 4, 9, 16, …, jedoch weisen beide Folgen bei genauem Hinsehen ein unterschiedliches Verhalten auf. Während zum Beispiel die Differenz zweier aufeinanderfolgender gerader Zahlen stets 2 ist, nehmen die Abstände der Quadratzahlen immer weiter zu, etwa 4 - 1 = 3, 9 - 4 = 5 und 16 - 9 = 7. Beide Folgen haben jedoch ein sehr reguläres Muster gemein, d. h., sie können über einfache Rechenoperationen bestimmt werden. Zum Beispiel ist die n-te gerade Zahl einfach 2n. Im Gegensatz dazu ist bis heute kein einfaches Muster unter der Folge 2, 3, 5, 7, 11, …, 59, 61, 67, … der Primzahlen entdeckt worden. Zum Beispiel gibt es kein „schnelles“ Verfahren, die n-te Primzahl zu berechnen. Es zeigt sich jedoch, dass es auf lange Sicht Muster unter den Primzahlen zu erkennen gibt. Betrachtet man also haufenweise Primzahlen zur gleichen Zeit, so können durch „Mittelwertbildung“ reguläre Strukturen erkannt werden.
Das Prinzip hinter dieser Tatsache ist von statistischer Natur. Statistik bedeutet hierbei, aus einer großen Menge von Daten Muster herauszufiltern, obwohl das „exakte Verhalten“ der einzelnen Datenobjekte (oder Subjekte) sehr kompliziert sein kann. In etwa sind alle Menschen sehr komplex, doch im Verhalten sehr vieler Menschen zur gleichen Zeit können Muster oftmals erkannt werden, die dann in Form von Wahrscheinlichkeiten auf Individuen zurück schließen lassen. Also geht es bei diesen Überlegungen zunächst um die Frage, wie die Verteilung der Primzahlen zu verstehen ist, mit anderen Worten, wie viele Primzahlen unterhalb einer vorgegebenen Schranke zu erwarten sind. Zum Beispiel sind nur 4 Primzahlen, nämlich 2, 3, 5 und 7, kleiner als die Zahl 10. Im Falle der oberen Schranke 150 gibt es schon 35 kleinere Primzahlen, nämlich
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149.

Dabei sind die insgesamt 20 Primzahlen zwischen 50 und 150 in grün markiert. Eine Frage der Zahlentheorie ist, ob es ein universelles und einfaches Prinzip gibt, zumindest zu schätzen, wie viele Primzahlen es unter einer gegebenen Schranke gibt. Erkannt wurde ein solches erstmals in den Jahren 1792/93 vom damals 15-jährigen Carl Friedrich Gauß,[12] nachdem dieser Logarithmentafeln studiert hatte. Gauß vermutete, dass die Anzahl aller Primzahlen von 2 bis zu einer großen Zahl x ungefähr dem Flächeninhalt zwischen der t-Achse und der Funktion im Intervall von 2 bis entspricht. Dabei ist der natürliche Logarithmus. Es gilt also die Integral-Näherung[13]
- Anzahl der Primzahlen bis
und allgemeiner für :
- Anzahl der Primzahlen zwischen und
Zum Beispiel gilt
womit sich die Formel wegen des exakten Wertes von 20 Primzahlen zwischen 50 und 150 (siehe oben in grün) ca. um den Wert 2 verschätzt. Das Integral von kann nicht elementar geschlossen berechnet werden, da der kehrwertige Logarithmus keine elementare Stammfunktion besitzt. Es definiert somit eine „eigenständige“ Funktion, die auch als Integrallogarithmus bekannt ist:
Bezeichnet die Primzahlfunktion, die für beliebige reelle Zahlen definiert ist als die Anzahl der Primzahlen, die nicht größer als sind, so wird die obere Aussage wie folgt präzisiert:
Für wachsende Werte von wird also der obere Quotient immer näher gegen 1 streben, also der relative Fehler der Schätzung gegen 0 gehen. Auch bei der „Statistik der Primzahlen“ gilt demnach der Grundsatz, dass größer werdende Datenmengen prozentual eine zuverlässigere Prognose erlauben. Gauß legte keinen mathematischen Beweis für diese Vermutung über die Primzahlverteilung vor, und es dauerte noch über 100 Jahre, bis ein solcher – unabhängig voneinander von Jacques Hadamard und Charles-Jean de La Vallée Poussin – im Jahr 1896 erbracht wurde.[14] Dabei bedeutet Beweis nicht, dass alle erdenklichen Werte durchprobiert wurden, was bei unendlich vielen Zahlen unmöglich ist, sondern dass ein auf den mathematischen Axiomen basierendes logisches Argument den Sachverhalt in voller Allgemeinheit belegt. Das damit gezeigte Theorem wird als Primzahlsatz bezeichnet.[13]
Wegen (für ) ist der Primzahlsatz deutlich stärker als der Satz des Euklid, da er nicht nur die Unendlichkeit der Menge aller Primzahlen impliziert, sondern auch eine quantitative Idee für deren Verteilung gibt. Im Gegensatz zum Satz des Euklid ist sein Beweis deutlich anspruchsvoller. Klassischerweise wird dieser mit Methoden der komplexen Analysis geführt, wobei Taubersätze ein wichtiges Hilfsmittel sind. Es existieren jedoch auch elementare Beweise, etwa von Paul Erdös und Atle Selberg aus dem Jahr 1949,[15][16] aber auch moderne, wie zum Beispiel von Florian K. Richter aus dem Jahr 2021.[17] Das Wort „elementar“ bezieht sich hierbei primär auf die Methodik und nicht den Schwierigkeitsgrad.[18] Die Riemannsche Vermutung ist wiederum eine weitreichende Verbesserung des Primzahlsatzes.
Varianten der Problemstellung Bearbeiten
Die Riemannsche Vermutung stellt eine starke Verschärfung des Primzahlsatzes dar. Das bedeutet, dass sie neben der von Logarithmen stammenden Verteilung der Primzahlen eine sehr exakte quantitative Beschreibung der Abweichungen von der im Primzahlsatz vorhergesagten Integralschätzung postuliert. Sie ordnet das Verhalten der Primzahlen in den Pseudozufall ein. Es existieren einige unterschiedliche und dennoch äquivalente Sichtweisen auf das Problem, die im Folgenden angeführt werden.
Der absolute Fehler im Primzahlsatz Bearbeiten
Wie oben bezeichnet die exakte Anzahl von Primzahlen unterhalb der Schranke und den Integrallogarithmus. Der absolute Fehler im Primzahlsatz bezeichnet die Differenz . Dabei gewährleistet der Absolutbetrag, dass nur positive Größen im Ergebnis entstehen, da man sich zunächst nur für die Größe des Fehlers und nicht dessen Vorzeichen interessiert. Der absolute Fehler muss im Gegensatz zum relativen Fehler
keinesfalls gegen 0 gehen. Der Quotient aus und strebt mit wachsendem gegen 1, da Quadrate schneller wachsen als lineare Terme, nicht aber die (sogar unbeschränkte) Differenz beider Terme. Die Riemannsche Vermutung macht eine detaillierte Aussage über den absoluten Fehler im Primzahlsatz.
Vermutung: Der absolute Fehler im Primzahlsatz ist „im Wesentlichen“ von der Ordnung einer Quadratwurzel.[19] Genauer gibt es eine Konstante , sodass für alle Werte die Abschätzung wahr ist, bzw. kürzer für .

Dabei bezeichnet den natürlichen Logarithmus von . Veranschaulicht werden kann diese Aussage wie folgt: Die Quadratwurzel halbiert ungefähr die Anzahl der Ziffern einer Zahl vor dem Komma (wegen in der Hochzahl!). Zum Beispiel hat 100 000 000 insgesamt 9 Ziffern vor dem Komma, aber seine Quadratwurzel 10 000 nur noch 5. Trifft die Riemannsche Vermutung zu, so sollte die Integralschätzung des Primzahlsatzes langfristig ungefähr in der „oberen Hälfte“ der Dezimalziffern vor der Null mit dem tatsächlichen Ergebnis übereinstimmen. Exakt berechnet wurde zum Beispiel , es gibt also ca. 18,4 Trilliarden Primzahlen unterhalb einer Quadrillion.[20][21] Ferner gilt:[19]
Von den insgesamt 23 Stellen vor dem Komma des exakten Wertes gibt es eine Übereinstimmung in den 12 ersten Ziffern mit dem Integrallogarithmus, oben in Blau markiert. Ab der ersten Abweichung sind die Ziffern vor dem Komma rot. Dabei ist 12 in etwa die Hälfte von 23. Diese Berechnung stützt also die Riemannsche Vermutung. Die logarithmischen Terme in der Abschätzung sowie bei sind im Vergleich zur Quadratwurzel so klein, dass dies nichts Wesentliches an dieser ungefähr hälftigen Aufteilung ändert.
Der Mathematiker Lowell Schoenfeld konnte einen passenden Wert für die zunächst unbestimmte Konstante in der Riemannschen Vermutung für hinreichend große Werte genau berechnen: Sollte diese zutreffen, so gilt[22]
- falls
Dabei bezeichnet die Kreiszahl. Ist die Vermutung also wahr, kann in oberer Formulierung im Wesentlichen bereits gesetzt werden.
Obwohl der Term für wachsende Werte immer weiter ansteigt, und damit der absolute Fehler auch beliebig anwachsen kann, besagt die Riemannsche Vermutung, dass dieser relativ betrachtet sehr klein ist, da
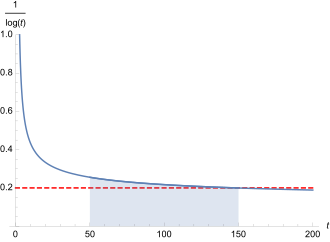
fast mit der Geschwindigkeit einer kehrwertigen Quadratwurzel gegen 0 strebt. Wie Jürgen Neukirch bemerkte, weist dies auf eine besondere „Glätte“ in der bildlichen Darstellung der Primzahlverteilung hin, wenn man die Skala hochsetzt.[23]
-
Auf kleiner Skala ist die Primzahl zählende Funktion sehr irregulär, und man sieht deutliche Sprünge. Jedes Mal, wenn eine Primzahl erreicht wird, springt die Treppenfunktion um den Wert 1 nach oben.
-
Auch bis x = 1000 sind noch Sprünge zu sehen, wenn auch kleiner
-
Auf sehr großer Skala wirkt die Kurve der Zählfunktion zunehmend glatt. Die Schwankungen um die absolut glatte Kurve von Li(x) werden relativ betrachtet kleiner, siehe nächstes Bild.
-
Im Gegensatz dazu sind die Schwankungen der Funktionendifferenz = Fehler stark ausgeprägt und gut zu sehen. Jedoch ist die Größe im Bereich um die 50 völlig vernachlässigbar, und somit erfasst die Skala des vorigen Bildes diese nicht mehr.
Eine zu verwandte und in der Theorie der Riemannschen Vermutung natürlichere Treppenfunktion wird wie folgt konstruiert. Man startet bei Null, und jedes Mal, wenn eine Primzahlpotenz erreicht wird, springt die Treppenfunktion um den natürlichen Logarithmus der betroffenen Primzahl nach oben. Zum Beispiel ist
- und .
Allgemein gilt die Definition
mit der Mangoldt-Funktion . Die Riemannsche Vermutung kann nun auch wie folgt formuliert werden.
Vermutung: Die Abweichung der Funktion von , Letzteres graphisch der Winkelhalbierenden des 1. Quadranten entsprechend, ist „im Wesentlichen“ von der Ordnung einer Quadratwurzel. Es gibt eine Konstante , sodass für alle , bzw. kürzer für .[24]
Obwohl die Definition der Funktion zunächst komplizierter ist, ist ihre Betrachtung aus mathematischer Sicht natürlicher. Ein Grund dafür ist der verhältnismäßig einfache Zusammenhang zwischen der Mangoldt-Funktion und der sog. Riemannschen Zeta-Funktion, die, auch aus Gründen der Einfachheit und Übersicht, ein essentielles Objekt im Themenkreis der Riemannhypothese ist (siehe unten).[25]
-
Schaubild der Funktion im Intervall . Für jede Primzahlpotenz, wie 2, 8 oder 9, gibt es einen Sprung. Die Sprünge haben je nach Primzahlpotenz unterschiedliche Höhe .
-
Schaubild der Funktion im Intervall zusammen mit der Ursprungsgeraden mit Steigung 1
-
Auf höherer Skala, wie etwa , wird die Ähnlichkeit zur Winkelhalbierenden immer deutlicher
Wahrscheinlichkeitstheoretische Interpretation Bearbeiten
Die Riemannsche Vermutung kann probabilistisch interpretiert werden. Dies geht auf den Mathematiker Arnaud Denjoy zurück.[26]
Der zentrale Grenzwertsatz Bearbeiten
Um den Zusammenhang zwischen den Primzahlen auf der einen Seite und der Wahrscheinlichkeitstheorie auf der anderen Seite zu verstehen, wird der zentrale Grenzwertsatz benötigt. Der einfachste Vergleich beider Konzepte entsteht über die Betrachtung eines fairen Münzwurfes. Es wird eine faire Münze mit den möglichen Ergebnissen „Kopf“ und „Zahl“ mehrmals hintereinander geworfen. In der idealen Situation ist das Ergebnis jeden Wurfs an sich absolut zufällig und außerdem hängen die Ergebnisse der Würfe nicht voneinander ab. Wurde also zunächst Kopf geworfen, soll dies unerheblich dafür sein, ob wieder Kopf oder auch Zahl folgt. Die in dieser Situation falsche Annahme, nach einer langen Strecke von „Kopf“-Würfen seien „Zahl“-Würfe wahrscheinlicher, ist indes als Spielerfehlschluss bekannt („der Zufall hat kein Gedächtnis“).
Unter Annahme absoluten Zufalls bei gleichen Wahrscheinlichkeiten und außerdem Unabhängigkeit der einzelnen Würfe kann bei häufigem Wiederholen eines Münzwurfes ein bestimmtes Muster beobachtet werden. Am besten wird dies veranschaulicht, wenn die Ereignisse „Kopf“ und „Zahl“ durch die Zahlen bzw. ersetzt werden und nach jeder Serie von Würfen die Summe aller Wurfergebnisse gebildet wird. Dies entspricht dann der Bilanz in einem Glücksspiel, in dem bei Kopf 1 Euro gewonnen und bei Zahl 1 Euro verloren wird. Werden „Kopf“ – „Kopf“ – „Zahl“ – „Zahl“ – „Kopf“ geworfen, liegt der Gewinn bei 1 Euro, denn
Gleichzeitig entspricht dies der Differenz aus geworfenen „Köpfen“ und „Zahlen“. Bei einer sehr großen Anzahl an Würfen, etwa 40 000, ist die Annahme naheliegend, dass jeweils ungefähr 20 000 Mal „Kopf“ und „Zahl“ geworfen wird, da beide Ergebnisse exakt gleiche Wahrscheinlichkeit haben. Dies hätte als mögliche Konsequenz, dass sich die Gewinnbilanz in etwa beim Wert Null „einpendelt“, da angenommen wurde, dass der Wert in etwa so häufig summiert wurde wie . Auf der anderen Seite ist es bereits in diesen Größenordnungen extrem unwahrscheinlich, dass etwa ein Ergebnis wie genau 20 000-mal Kopf und genau 20 000-mal Zahl auftritt, was einer Gewinnbilanz von exakt 0 entspräche. Es ist eher damit zu rechnen, dass der Zufall zu „Gunsten“ von „Kopf“ oder „Zahl“ einen gewissen „Ausreißer“ verursachen wird. Das bedeutet, dass nach der Wurfserie sehr wahrscheinlich eine gewisse Größe häufiger gefallen sein wird als die andere, obwohl zu Beginn gleiche Wahrscheinlichkeiten vorlagen. Die Größe dieses „Ausreißers“ ist Gegenstand des zentralen Grenzwertsatzes: Bezeichnet die Zufallsgröße mit dem Wert des -ten Wurfes, so errechnet sich der Gewinn des oberen Spiels mit Münzwürfen durch

Beginnt der Spieler mit 0 Euro auf dem Konto, kann auch als Kontostand nach Würfen interpretiert werden. Der zentrale Grenzwertsatz trifft eine Aussage über das zu erwartende Verhalten des Gewinns , wenn beliebig groß wird. Ihm zufolge liegt die Größenordnung von stets im Umfeld der Quadratwurzel der Wurfanzahl ; genauer gilt für die Wahrscheinlichkeit, dass , die Näherung[27][Anm. 2]
Dem Integral liegt die Verteilungsfunktion der Standardnormalverteilung zugrunde. Wird zum Beispiel eine Münze 40 000 Male hintereinander geworfen, so ist die Wahrscheinlichkeit, dass der Kontostand am Ende im Bereich liegt wegen ungefähr 68,2 % (siehe Bild rechts, die Abweichung ist hier ). Negative Zahlen auf dem Konto werden als Schulden verstanden.
-
Eine mögliche Entwicklung des Kontostands im Laufe eines Spiels mit 40 000 Münzwürfen entspricht mathematisch einer Irrfahrt. Zur Größenorientierung sind die Funktionen in grün bzw. orange mit eingetragen. Kurz vor Ende des Spiels beobachtet man eine „Pechsträhne“. Extreme Ereignisse, wie ein steiler Anstieg bis 40 000 (nur „Kopf“), sind zwar nicht unmöglich, aber sehr unwahrscheinlich und entsprechen nicht einem „typischen Verlauf“ des besagten Spiels.
Der zentrale Grenzwertsatz findet anschaulich den „Mittelweg“ zwischen zwei extremen und jeweils äußerst unwahrscheinlichen Ereignissen: einmal, dass (fast) genau so häufig „Kopf“ wie „Zahl“ geworfen wird, oder zweitens, dass „sehr viel“ häufiger „Kopf“ als „Zahl“ geworfen wird oder umgekehrt. Es stünde ein zu reguläres Verteilungsmuster mit der geforderten Unabhängigkeit der Würfe in Konflikt, und ein zu starkes Abweichen vom Mittelwert 0 mit der ebenfalls geforderten gleichen Wahrscheinlichkeit. Die Bestimmung der genauen Größenordnung ist kein einfaches Unterfangen, und Gegenstand des Beweises des zentralen Grenzwertsatzes, der mit Methoden der höheren Analysis geführt wird.[28]
Wegen der über die Normalverteilung gegebenen Wahrscheinlichkeiten gilt insbesondere für jede Zahl :
- mit Wahrscheinlichkeit 100 % (in einem asymptotischen Sinn).
Dabei ist die Potenzschreibweise zu beachten.
Primzahlen und Pseudozufall Bearbeiten
Eine „Verbindung“ zwischen Primzahlen und dem wiederholten Münzwurf kann im Sinne des zentralen Grenzwertsatzes wie folgt hergestellt werden.[29] Es werden nacheinander die natürlichen Zahlen betrachtet; und zwar in deren eindeutiger Primfaktorzerlegung. Jedes Mal, wenn die Anzahl der Faktoren gerade ist, wird dies als gewertet, und wenn sie ungerade ist, als . Über dieses Prozedere lässt sich eine Funktion auf den natürlichen Zahlen definieren:
- , wobei Anzahl der Primfaktoren von .
Diese wird auch als Liouville-Funktion bezeichnet, benannt nach Joseph Liouville.[30] Zu beachten ist, dass ein Produkt mit einer ungeraden Anzahl aus lauter Faktoren −1 wieder −1 ist, und eines mit einer geraden Anzahl an Faktoren −1 genau +1, da Minus mal Minus Plus ergibt. Zum Beispiel hat die Zahl insgesamt fünf Primfaktoren, denn
und daher gilt . Die folgende Tabelle zeigt den Sachverhalt für einige weitere Werte von .
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | … | 236 | 237 | 238 | 239 | … | 174.635.999 | 174.636.000 | 174.636.001 | 174.636.002 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Primfaktorzerlegung | – | 2 | 3 | 22 | 5 | 2·3 | 7 | 23 | 32 | 2·5 | 11 | 22·3 | … | 22·47 | 3·79 | 2·7·17 | 239 | … | 29·379·15.889 | 25·34·53·72·11 | 174.636.001 | 2·17·71·73·991 | … |
| Faktoranzahl Ω(n) | 0 | 1 | 1 | 2 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 3 | … | 3 | 2 | 3 | 1 | … | 3 | 15 | 1 | 5 | … |
| λ(n) = (–1)Ω(n) | 1 | −1 | −1 | 1 | −1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 | … | −1 | 1 | −1 | −1 | … | −1 | −1 | −1 | −1 | … |
Das genaue Verhalten der Primfaktorzerlegungen ist, für größer werdende Zahlen, ohne eine sehr aufwändige Berechnung nicht vorherzusagen und unterliegt starken Schwankungen. Die Riemannsche Vermutung besagt, dass die von der Liouville-Funktion definierte Folge pseudozufällig ist.[31][30] Sie ist zwar determiniert, kann also theoretisch berechnet werden und ihre Werte „liegen alle bereits fest“, dennoch ähnelt sie in ihren Eigenschaften einem sogenannten Random Walk.[32] Damit, so die Vermutung, sollten sich die aufaddierten Werte der Liouville-Funktion auf lange Sicht ungefähr wie ein „typischer Verlauf“ des oben beschriebenen Glücksspiels mit einem fairen Münzwurf verhalten.[30] Es kann für
festgehalten werden:
Vermutung: Es gilt, im Sinne des zentralen Grenzwertsatzes, für jedes beliebige . Äquivalent ist die Aussage, dass es für alle eine Konstante gibt, sodass die Ungleichung für alle gilt, kurz .[33]
Diese Form der Pseudozufälligkeit sagt anschaulich aus, dass sich Primzahlen in ihren Eigenschaften, wie Verteilung und Primfaktorzerlegung, „möglichst zufällig“ und „möglichst unabhängig“ verhalten. So soll zum Beispiel die Frage, ob sich eine zufällig gewählte Zahl in eine gerade oder in eine ungerade Anzahl an Primfaktoren zerlegen lässt, für wachsende Größe von mit „gleicher Wahrscheinlichkeit“ beantworten lassen.[30] Gleichzeitig sollen die Werte und für wachsende Werte „unabhängig“ sein. Also soll es keine einfache Möglichkeit geben, aus dem Verhalten des einen Wertes, das Verhalten des anderen zu ermitteln. Betrachtet man zum Beispiel
und den Nachfolger
- ,
so ist nicht unmittelbar ersichtlich, wie die Anzahlen der Primfaktoren kausal zusammenhängen.
-
Die Funktion bis x = 40 000 zusammen mit (orange). Etwa zwischen 18 000 und 20 000 gibt es ein gehäuftes Auftreten von Zahlen mit einer geraden Anzahl an Primfaktoren, das sich aber mit den üblichen Schwankungen eines Zufallsprozesses rechtfertigen lässt.
Wäre die Riemannsche Vermutung falsch, so gäbe es ein Ungleichgewicht in der Primzahlverteilung in dem Sinne, dass es zum Beispiel streckenweise unnatürlich viel gehäufter Zahlen mit einer geraden Anzahl an Primfaktoren, wie 10, 14, 25, 132, gäbe, als Zahlen mit einer ungeraden Anzahl an Primfaktoren, wie 7, 8, 12, 18 und 125. Das Scheitern der Riemannschen Hypothese würde die Verteilung der Primzahlen durcheinander bringen.[34]
Analog kann die Riemannhypothese auch für die Möbius-Funktion formuliert werden. Diese nimmt für Zahlen, die in eine ungerade bzw. gerade Anzahl paarweise verschiedener Primzahlen zerfallen, den Wert bzw. an, und wird für Zahlen, die mehrfach durch denselben Primteiler teilbar ist, . Es ist also zum Beispiel , und , da im letzten Fall die 3 mehr als einmal auftauchte.
Die Riemannsche Vermutung trifft genau dann zu, wenn für alle die Beschränkung für erfüllt ist.
Auch hier wird also eine Form der Pseudozufälligkeit vermutet.
Der Begriff der „Zufälligkeit“ unter den Primzahlen ist bis heute in erster Linie auch in Fachkreisen eine Anschauung, und bisher weder vollständig verstanden noch rigoros beschrieben worden. Heuristisch lassen sich einige wichtige Probleme, wie die Bestätigung der Goldbachschen Vermutung, aus dieser Eigenschaft herleiten, jedoch führt die gleiche Heuristik in anderen Fällen zu Widersprüchen.[35][36]
Der Weg über unendliche Reihen Bearbeiten
Um Fragen zu Primzahlen mit Mitteln der Analysis angreifen zu können, sind unendliche Reihen ein erstes Werkzeug.
Allgemeines zu Reihen Bearbeiten
Unter einer Reihe versteht man, veranschaulicht, eine niemals endende Summe von Zahlen. Dies können reelle, aber auch komplexe Zahlen sein. Die Dezimalschreibweise einer reellen Zahl kann als Reihe aufgefasst werden, etwa
oder auch
mit der Kreiszahl . Die durch die Punkte angedeuteten Summen enden niemals, da die Dezimalentwicklung von periodisch und die Kreiszahl irrational ist. Es gibt Reihen, die nicht geschlossen als Zahl darstellbar sind, etwa
aber auch solche, die gegen einen Grenzwert konvergieren (wie die oberen Beispiele mit Grenzwerten bzw. ). Reihen wie , die nicht konvergieren, nennt man divergent. Veranschaulichend gesagt kann eine Reihe nur dann konvergieren, falls die Glieder „schnell genug gegen 0 streben“. Aber nicht jede Reihe, deren Glieder gegen 0 streben, konvergiert, wie man an der harmonischen Reihe
sieht.

Einige Reihen spielen eine ganz besondere Rolle in der Mathematik, zum Beispiel die geometrische Reihe, die aufgrund der Euler-Produkte auch im Kontext der Riemannhypothese bedeutsam ist: Das Prinzip ist, zu einer Zahl alle natürlichen Potenzen aufzuaddieren. Man erhält dann
Es ist also zu jedem mit möglich, den Grenzwert der geometrischen Reihe geschlossen anzugeben. Es handelt sich auch um ein erstes Beispiel, dass eine Funktion durch eine Reihe definiert ist: man hat
und die Reihenglieder hängen sämtlich von ab. Die geometrische Reihe ist damit das Beispiel und , wobei für den ersten Summanden die Regel (und formal ) zu beachten ist.
Der Majorantentest und partielle Summation Bearbeiten
Die Bestimmung des Grenzwertes einer Reihe ist im Allgemeinen nicht einfach, doch in manchen Fällen ist bereits die Frage der Konvergenz schwer zu beantworten. In der Geschichte der Mathematik wurden Kriterien entwickelt, zu entscheiden, ob gewisse Reihen konvergieren oder nicht. Eines davon ist der Majorantentest: Dieser basiert auf der einfachen Überlegung, dass eine unendliche Summe nicht-negativer Zahlen, die nach oben beschränkt ist, bereits konvergieren muss. Ist also eine Zahlenfolge und für alle , so gilt:
- konvergiert konvergiert.
Anschaulich gehen die Werte für Konvergenz schnell genug gegen 0, weshalb es wegen auch die Werte tun müssen. Eine wichtige Folgerung dieses Prinzips ist, dass aus der Konvergenz der Reihe über die Absolutbeträge notwendigerweise schon die Konvergenz der Reihe folgt. Eine besonders wichtige Majorante ist die Reihe
die für reelle Zahlen konvergiert, was mit dem Integralkriterium gesehen werden kann. Sie kann dazu dienen, die Konvergenz sog. Dirichlet-Reihen nachzuweisen.

Eine andere Technik betrifft den Umgang mit Reihen der Form
Dabei werden die Folgen und „separiert“:
- wobei , sofern .
Dieser Umordnungstrick geht auf den Mathematiker Niels Henrik Abel zurück und wird als partielle Summation bezeichnet. Rückwirkend bestätigen lässt sich dies durch sukzessives Ausmultiplizieren und Verrechnen der Terme. Dieser Trick kommt vor allem dann zum Einsatz, wenn die Zahlen „schwanken“ (etwa ständige Vorzeichenwechsel), womit deren Summen verhältnismäßig klein sind, während die Zahlen sukzessive kleiner werden, da dann die Differenzen eventuell viel schneller gegen Null streben als die selbst. Die notwendige Bedingung besagt ihrerseits, dass das Abklingen der gegen Null das Wachstum des Terms dominiert.
Zusammenfassend lässt sich, sofern die Nebenbedingung erfüllt ist, mit und folgende Variante des Majorantentests anführen:[37]
- konvergiert konvergiert konvergiert.
Die Riemannsche Vermutung und Reihenkonvergenz Bearbeiten
Im Rahmen der Riemannhypothese ist die Reihe
von Interesse, wobei die Liouville-Funktion bezeichnet. Diese ist jedoch nicht konvergent, da die nicht gegen Null streben. Allerdings kann man den Summanden weitere Terme hinzufügen, die dann Konvergenz erzwingen. Hängen die hinzugefügten Terme noch von einer Variablen ab, kann aus der zu untersuchenden Folge eine Funktion erzeugt werden. Etwa ist auch
nicht konvergent, doch betrachtet man die zugehörige Potenzreihe, ergibt sich für die Funktion
- .
Wie die Primzahlen selbst schöpft die Liouville-Funktion Struktur aus Gesetzen multiplikativer Art. Es gilt das Gesetz , sie ist also eine streng multiplikative Funktion. Diese Eigenschaft bietet mathematisch viele Vorteile und muss daher für die weitere Analyse erhalten bleiben. Statt also Terme mit konstanter Basis und veränderlichem Exponenten hinzuzufügen, werden Ausdrücke mit veränderlicher Basis und konstantem Exponenten in Betracht gezogen. Mit den Potenzgesetzen folgt damit
und die Multiplikativität bleibt beim Übergang erhalten. Historisch bedingt werden die Exponenten mit statt bezeichnet und man nennt den resultierenden Reihentyp auch Dirichlet-Reihe. Dirichlet-Reihen können mit partieller Summation gut analysiert werden: Es sind Potenzfunktionen in , und durch Nehmen der Differenzen werden diese um den Faktor kleiner:
- (zum Beispiel wird aus eine lineare Funktion, und dieses Prinzip überträgt sich von auf beliebige Exponenten).
Dabei bedeutet das Zeichen , dass die linke Seite bis auf einen von abhängigen aber von unabhängigen Faktor stets kleiner ist als die rechte Seite. Der zusätzliche Faktor macht den Term um eine Potenzgrößenordnung kleiner als . Setzt man weiter mit der Liouville-Funktion, so haben diese Vorzeichenwechsel. Die Häufigkeit des Wegkürzens der Terme innerhalb steht mit der Anzahl der Zahlen mit gerader bzw. ungerader Primfaktoranzahl unterhalb in direktem Zusammenhang, und die Riemannsche Vermutung (RV) besagt für alle (siehe oben). Setzt man diese voraus, gilt für alle die Nebenbedingung und es folgt für eben diese mit Majorantentest und partieller Summation:
- konvergiert.
Im letzten Schritt kann so klein gewählt werden, dass wird, etwa durch . Die gleichen Überlegungen gelten für die Möbius-Funktion. Daraus motiviert sich:
Vermutung: Die Reihen bzw. konvergieren für alle .
Mit folgert man für mit dem Majorantentest
weshalb die betroffene Reihe hier „trivialerweise“ konvergiert. Gleiches gilt für die Möbius-Funktion. Dieses einfache Verfahren ist für nicht mehr möglich. Bereits der Fall ist schwierig und fruchtet durch eine zahlentheoretische Folgerung: Aus der Konvergenz der Reihe
gegen den Grenzwert 0 kann der Primzahlsatz gefolgert werden. Dass der Grenzwert tatsächlich 0 ist, fällt als „Beigabe“ beim Beweis der Konvergenz mit heraus.[38] Über die Fälle ist bis heute nichts bekannt. In diesem Sinne ist die Riemannsche Vermutung auch in dieser Hinsicht eine deutliche Verschärfung des Primzahlsatzes.
Formulierung über die Holomorphie von Dirichlet-Reihen Bearbeiten
In ihrer ursprünglichen Fassung ist die Riemannsche Vermutung zunächst kein Problem der Zahlentheorie, sondern ein Problem der komplexen Analysis. Die komplexe Analysis beschäftigt sich mit den Eigenschaften holomorpher Funktionen, sowie sich die klassische (reelle) Analysis mit den Eigenschaften differenzierbarer Funktionen beschäftigt.
Die Riemannhypothese besagt unter anderem, dass die Dirichlet-Reihe der Liouville-Funktion
eine in einem „möglichst großen Bereich“ holomorphe Funktion darstellt. Dabei ist „großer Bereich“ näher zu spezifizieren. Ähnlich wie die Konvergenzfrage im Reellen misst die Holomorphie das Verhalten der Reihe , und ein großer Holomorphiebereich impliziert ein „starkes“ gegenseitiges Wegheben der Terme in dieser Reihe.
Um Dirichlet-Reihen als holomorphe Funktionen zu sehen, müssen diese auch an komplexen Zahlen ausgewertet werden. Unter Verwendung der Formel von Euler, die imaginäre Zahlen im Exponenten sinnvoll interpretiert, gelingt dies für wie folgt:
Die Vorschrift im Komplexen für eine Dirichlet-Reihe lautet also
Wegen der Beschränktheit von Sinus und Kosinus für reelle Zahlen sieht man damit, dass sich das Verhalten von für festen Realteil aber veränderlichen Imaginärteil im Exponenten nur „geringfügig ändert“. Der Realteil von bestimmt die absolute Größe des Terms , während der Imaginärteil nur eine „Schwingung“ erzeugt, die in der komplexen Ebene als Drehung entlang des Einheitskreises verstanden werden kann. Genau genommen gilt . Bei wachsendem Realteil von nähern sich die Terme zunehmend der Null, weshalb die Konvergenzbedingungen „immer besser werden“. Unter anderem mit dieser Beobachtung kann eine bedeutende Eigenschaft für Funktionen gezeigt werden, die durch eine Dirichlet-Reihe definiert sind: Konvergiert eine Dirichlet-Reihe an einer Stelle , so tut sie das bereits an jeder Stelle mit , wobei an den Imaginärteil keine besonderen Bedingungen gestellt sind. Im Innern ihres Konvergenzbereichs stellt sie eine holomorphe Funktion dar.
Es folgt damit, dass Dirichlet-Reihen auf offenen Halbebenen der komplexen Ebene konvergieren und dort holomorph sind. Konvergiert eine Dirichlet-Reihe irgendwo, so gibt es ferner eine eindeutig bestimmte Zahl , die sogenannte Konvergenzabszisse, so dass die Dirichlet-Reihe für alle komplexen Zahlen mit konvergiert, und für alle mit divergiert. Über die Fälle kann keine allgemeine Aussage getroffen werden. Hiermit ergibt sich eine weitere Formulierung der Riemannhypothese. Ist die Reihe für alle konvergent, so auch für alle mit , und umgekehrt.
Vermutung: Die Reihen und konvergieren für alle mit , und insbesondere ist die von der Liouville- bzw. Möbius-Funktion erzeugte Dirichlet-Reihe in der Halbebene holomorph.
Für den Primzahlsatz wird lediglich die holomorphe Fortsetzbarkeit in den Bereich benötigt.[39] Über diese erste funktionentheoretische Fassung ist es möglich, den Zusammenhang zwischen der Primzahlverteilung und Nullstellen der sogenannten Riemannschen Zeta-Funktion zu formulieren.
Primzahlen und die Nullstellen der Zeta-Funktion Bearbeiten
Wie Bernhard Riemann bereits 1859 erkannte, besteht eine enge Verbindung zwischen Primzahlen und den Nullstellen einer bestimmten Funktion. Diese trägt den Namen Riemannsche Zeta-Funktion, und wird mit dem griechischen Buchstaben Zeta (klein) notiert; also . Es ist die Variablenbenennung im Kontext der Zeta-Funktion jedoch unüblich, da sie nicht nur reelle Zahlen entgegennimmt und abbildet, sondern auch komplexe Zahlen. Als Variable hat sich im Laufe der Zeit die von Riemann gewählte Benennung durchgesetzt, wobei (Sigma) der Realteil und der Imaginärteil von ist. Das Symbol bezeichnet wie üblich die imaginäre Einheit und erfüllt . Eine (komplexe) Nullstelle der Zeta-Funktion erfüllt die Gleichung .
Die Riemannsche Zeta-Funktion Bearbeiten

Die Riemannsche Zeta-Funktion wird in der Literatur als diejenige Dirichlet-Reihe definiert, deren Koeffizienten ausschließlich 1 sind, mit anderen Worten
Mit dem Majorantentest sieht man, dass die Reihe für alle Werte mit konvergiert. An der Stelle erhält man gerade die harmonische Reihe:
also gilt , damit ist die Konvergenzabszisse von , und die Dirichlet-Reihe wird die Zeta-Funktion nicht mehr für Zahlen mit darstellen. Für manche Werte im Konvergenzbereich konnten geschlossene Funktionswerte der Zeta-Funktion berechnet werden. So fand Leonhard Euler zum Beispiel
- und
mit der Kreiszahl .
Für die Zahlentheorie ist es bedeutsam, die Zeta-Funktion auch in größeren Bereichen betrachten zu können als nur die um 1 verschobene rechte Halbebene. Es kann gezeigt werden, dass sie eine Fortsetzung besitzt, die auch für Zahlen definiert ist, für welche die Dirichlet-Reihe nicht mehr konvergiert. Lediglich der Wert ist weiterhin auszuschließen, für alle anderen komplexen Zahlen ist mit der Fortsetzung allerdings definiert. Die Fortsetzung ist für alle holomorph, und damit wegen des Identitätssatzes für holomorphe Funktionen bereits eindeutig bestimmt, da der Definitionsbereich wegzusammenhängend ist. Es gibt also weiterhin nur „die eine“ Zeta-Funktion. Hintergrund der Fortsetzungsmöglichkeit ist, dass das verwandte Integral
- , falls ,
offenbar für alle fortgesetzt werden kann, mit komplexer Ableitung . Es sind aber die Funktionen
- und
„ähnlich genug“, dass aus den „guten Fortsetzungseigenschaften“ des Integrals auch die Fortsetzbarkeit von gefolgert werden kann, obgleich die mathematischen Details bei diesem Unterfangen weitaus technischer sind.

Eine weitere, auch für die Riemannsche Vermutung, bedeutsame Eigenschaft der Zeta-Funktion wurde bereits von Euler beobachtet, jedoch erst durch Riemann bewiesen. Die Zahlenwerte und stehen in enger Verbindung über die sogenannte Funktionalgleichung der Zeta-Funktion:[40]
Dabei ist die Gammafunktion und die Kreiszahl. Diese Gleichheit ist als global gültige Identität im Sinne des Beispiels , und nicht als Gleichung zu verstehen, wobei letztere nur für einige wenige Lösungen gelten könnte. Ebenfalls bemerkenswert ist, dass beide Terme in der Funktionalgleichung über den Variablenwechsel auseinander hervorgehen. Die Zeta-Funktion besitzt demnach ein Spiegelungsverhalten an der Geraden , die unter der Spiegelung unverändert bleibt.
Das Euler-Produkt Bearbeiten
Ihre zahlentheoretische Bedeutung erhält die Zeta-Funktion über das Euler-Produkt. Namensgeber Leonhard Euler entdeckte als erster diesen Zusammenhang, ohne jedoch dessen tiefere Bedeutung in vollem Umfang zu erkennen. Erst Bernhard Riemann konnte, da er die Zeta-Funktion als holomorphe Funktion in den komplexen Zahlen begriff, den Zusammenhang voll ausschöpfen. Hintergrund ist, dass für ein Studium der unendlich vielen Primzahlen alternativ ein einzelnes mathematisches Objekt analysiert werden kann, das Informationen zu jeder Primzahl in sich kodiert, und zwar gleichzeitig. Solche Objekte werden in der Zahlentheorie auch als globale Objekte bezeichnet. Genau ein solches Objekt ist die Riemannsche Zeta-Funktion.
Das Euler-Produkt ist eine alternative Darstellung der Zeta-Funktion im Konvergenzbereich der Dirichlet-Reihe. Als Formel geschrieben lautet es:
- wobei .
Dabei ist das Produktzeichen, und das rechte Produkt erstreckt sich über genau alle Primzahlen. Für unendliche Produkte (nach Euklid gibt es unendlich viele Primzahlen) gelten ähnliche Anschauungen wie für Reihen, nur dass die Faktoren („Glieder des Produktes“) im Laufe der Zeit gegen 1 streben müssen, falls das betroffene Produkt konvergieren soll, da Faktoren nahe 1, genau wie Summanden nahe 0, nur noch wenig am Zwischenwert ändern. Das Euler-Produkt ergibt sich aus der geometrischen Reihe sowie dem Fundamentalsatz der Arithmetik. Es ist andersherum eine analytische Formulierung der Tatsache, dass jede natürliche Zahl eine eindeutige Primfaktorzerlegung besitzt, wobei die Eindeutigkeit durch die im Zähler des Terms innerhalb der Zeta-Reihe ausgedrückt wird.
| Für die detaillierte Herleitung |
|
Für die formale Herleitung des Euler-Produktes werden lediglich die geometrische Reihe (siehe oben), der Satz, dass jede natürliche Zahl genau eine Zerlegung als Produkt von Primzahlen besitzt, sowie Ausmultiplizieren von Klammern benötigt. Zu Beginn bewährt es sich, nur eine endliche Anzahl von Primzahlen im Produkt zu beachten. Entwickelt man jeden Term als eine geometrische Reihe , so ergibt sich im Falle nur einer Primzahl wobei das Potenzgesetz zu beachten ist. Zur Rechten stehen genau die Zahlen, die ausschließlich Zweien in ihrer Primfaktorzerlegung haben, also die Zweierpotenzen. Verfährt man weiter mit den ersten zwei Primzahlen, ergibt sich Multipliziert man beide Klammen aus, ergeben sich in der Summe alle Kombinationen von Termen der Form mit , es gilt also und auf der rechten Seite stehen genau alle Terme , sodass nur Zweien und Dreien in seiner Primfaktorzerlegung hat. Beim Ausmultiplizieren wird jeder Summand der einen Klammer mit einem Summand der anderen Klammer verrechnet, und das in jeder Kombination, für sind die entsprechenden Terme in Rot markiert. Auf ähnliche Weise findet man, dass zu der entsprechenden Dirichlet-Reihe korrespondiert, in der alle Zahlen mit Primfaktorzerlegung auftauchen, und so weiter. Entsprechend gilt für allgemein die ersten Primzahlen Nun kann man in dieser Formel gegen Unendlich laufen lassen, und erhält da jede Zahl genau eine Zerlegung besitzt. |

Eine wichtige Folgerung des Euler-Produktes für die Analysis der Zeta-Funktion ist, dass für alle gilt. Dies ist eine Konsequenz einer Erweiterung des Satzes vom Nullprodukt für unendliche Produkte: keiner der Faktoren des Euler-Produktes ist für irgendeinen Eingabewert aus diesem Bereich null, also wird es auch nicht im Grenzwert Null sein. Weitaus nichttrivialer ist die Tatsache, dass das Euler-Produkt, im Gegensatz zur Dirichlet-Reihe, auch auf der Geraden , mit Ausnahme von , an Gültigkeit behält. Es gilt[41]
was die Nullstellenfreiheit von im gesamten Bereich zur Folge hat. Als eine Folgerung der Funktionalgleichung ergibt sich, dass die einzigen Nullstellen von außerhalb des sog. kritischen Streifens die trivialen Nullstellen
sind. Alle anderen Nullstellen bezeichnet man als nichttrivial, und diese liegen allesamt im kritischen Streifen.[42]
Der Zusammenhang mit der Liouville- und der Möbius-Funktion Bearbeiten
Der große Nutzen des Euler-Produktes besteht darin, dass sich mit seiner Hilfe einfache Verbindungen zwischen der Zeta-Funktion und zahlentheoretischen Funktionen, wie der Liouville-Funktion, aufstellen lassen. Diese ist eine vollständig multiplikative Funktion, also gilt für alle natürlichen Zahlen und , da das Produkt genau Primfaktoren hat, aber . Über die verallgemeinerte Form des Euler-Produktes für vollständig multiplikative Funktionen ergibt sich damit[43][44]
| Für die detaillierte Herleitung |
|
Zunächst betrachtet man den Term Wegen Punkt vor Strich scheint eine weitere Umformung dieses Termes in Summenform (= Striche) vergebens. Im Gegensatz dazu können Produkte (= Punkte) in Zähler und Nenner manipuliert und verrechnet werden. Man erhält mit dem Euler-Produkt Im Schritt wurde dabei die Regel Primzahl für Primzahl angewendet, und in Schritt der Doppelbruch aufgelöst. Mit der dritten binomischen Formel erhält man und folglich wobei sich die Terme in rot kürzten. Das zusammenfassende Resultat lässt sich erneut mit der geometrischen Reihe deuten: im Gegensatz zum Euler-Produkt für hat sich in dieser Formel „nur“ das Vorzeichen vor von Minus zu Plus geändert. Setzt man statt in die geometrische Reihe, erhält man womit die Vorzeichen in der hinteren Reihe alternieren, d. h. abwechseln. Erneut können die Klammern sukzessive ausmultipliziert werden, nur dass für jede Primzahlpotenz ein Vorzeichen mitgenommen wird. Also korrespondiert im Ergebnis zum Vorzeichen : Es ist etwa , denn hat 5 Primfaktoren, und es gilt . Damit findet man[44]
|
Auf sehr ähnlichem Weg lässt sich auf die erzeugende Dirichlet-Reihe der Möbius-Funktion als rationale Funktion der Zeta-Funktion geschlossen ausdrücken:
Formulierung über Nullstellen der Zeta-Funktion Bearbeiten
Mittels Euler-Produkt kann die Dirichlet-Reihe der sehr komplizierten Liouville-Funktion bzw. Möbius-Funktion geschlossen als rationale Funktion in Zeta-Funktionen ausgedrückt werden. Gleichzeitig besagt die Riemannsche Vermutung, dass sich der Term bzw. holomorph auf den Bereich fortsetzen lassen kann. Damit ist ausgeschlossen, dass der Nenner in diesem Bereich null wird, da es der Zähler wegen des Euler-Produktes auch nicht sein kann. Es wird folglich vermutet:

Vermutung: Alle Nullstellen der Riemannschen Zeta-Funktion erfüllen .
Aus der Funktionalgleichung der Zeta-Funktion geht hervor, dass genau dann wenn für den Fall , da sowohl die Gammafunktion als auch die Exponentialfunktion in diesem Bereich weder Pol- noch Nullstellen haben, sich also „neutral verhalten“. Gäbe es also zum Beispiel eine Nullstelle mit , so wäre mit die Riemannsche Vermutung verletzt. Einzig die Gerade bleibt unter der Transformation unverändert. Hieraus motiviert sich folgende hinreichende Version der Riemannschen Vermutung:
Vermutung: Alle Nullstellen der Riemannschen Zeta-Funktion im Streifen erfüllen .
Die Funktion ist ganz und nimmt an reellen Stellen reelle Werte an. Ergo hat sie im Punkt bloß reelle Ableitungen. Daraus folgt , wobei der Überstrich die komplexe Konjugation bedeutet (Spiegelung an der reellen Achse). Ist also eine nichttriviale Nullstelle der Zeta-Funktion, so auch . Wird dies mit der Funktionalgleichung kombiniert, treten die nichttrivialen Nullstellen zunächst in Vierergruppen auf (siehe Bild). Stimmt aber die Riemannsche Vermutung, verschmilzt dies wegen und entsprechend zu lediglich einer Zweiergruppe.[45]
Dies ist die auf Bernhard Riemann zurückgehende Originalformulierung. Sie motivierte sich weder aus der Restgliedabschätzung des Primzahlsatzes noch aus den für die Liouville-Funktion vermuteten Beschränktheitseigenschaften. Beide Alternativformulierungen wurden jedoch einige Jahre später als Konsequenz des vermuteten Nullstellenverhaltens der Zeta-Funktion gefolgert und sind zu diesem sogar äquivalent.
Riemann kam auf seine Vermutung bei der Untersuchung des Produkts der Zeta-Funktion mit der Gammafunktion[46]
- ,
wobei er setzte, und erhielt damit für alle mittels der Funktionalgleichung:
Es ist also eine gerade Funktion.[47] Es ist aber auch , da für reelle reellwertig ist. Der Faktor neutralisiert die trivialen Nullstellen und die Polstelle von , womit sich in diese Punkte holomorph fortsetzt, aber dort nicht verschwindet.[48] Das führt zu folgender einfacheren Form:[49]
Vermutung: Sämtliche Nullstellen der Funktion in der komplexen Ebene sind reell.
Riemann sprach von „reellen Wurzeln“ der Gleichung und meinte damit, dass für ein im kritischen Streifen die besagte Gleichung lediglich für reelle , also , zu lösen sei.
-
Schaubild der Funktionen (in blau) und (in orange) im Intervall . Eine komplexe Zahl ist genau dann Null, wenn Real- und Imaginärteil Null sind. Eingezeichnet sind die ersten 6 Nullstellen der Funktion , hier erkennbar als Riemanns „reelle Wurzeln“.
-
Komplexes Schaubild der Funktion im Bereich und . Die kritische Gerade entspricht, wegen des Variablenwechsels , nun der reellen Achse, die gestrichelt eingezeichnet ist. Der kritische Streifen wird von weißen Linien eingeschlossen. Die ersten 6 Nullstellen, als schwarze Punkte und durch eingezeichnete Pfeile erkennbar, liegen auf der kritischen Geraden (für genaue Koordinaten siehe auch das obere „reelle Bild“).
Die ersten nichttrivialen Nullstellen mit positivem Imaginärteil, nach dessen Größe geordnet, sind
Wegen ist zu beachten, dass auch Nullstellen vorliegen, wenn der Imaginärteil negativ gewählt wird. Für weitere Nullstellen siehe auch die Liste der nichttrivialen Nullstellen der Zeta-Funktion.
Nachbemerkungen Bearbeiten
Nullstellenordnungen Bearbeiten
Ebenfalls ungeklärt ist die Frage, welche Ordnungen die nichttrivialen Nullstellen der Zeta-Funktion haben. Es wird vermutet, dass sie alle die Ordnung 1 haben, also einfache Nullstellen sind.[50] Dies ist äquivalent dazu, dass die Ableitung an jeder nichttrivialen Nullstelle selbst nicht Null wird. Numerische Untersuchungen stützen diese Vermutung: alle bisher gefundenen Nullstellen hatten einfache Ordnung.
Im Falle der trivialen Nullstellen ist bereits bekannt, dass diese sämtlich einfach sind.[51]
Die Rolle der Zahl 1/2 Bearbeiten
Die Zahl spielt eine Schlüsselrolle in einigen Formulierungen der Riemannschen Vermutung. Zusammenfassend wird als Synthese der oberen Abschnitte festgehalten:
- Der Integrallogarithmus stimmt langfristig mit der Primzahl zählenden Funktion in der oberen Hälfte der Ziffern vor dem Komma überein, denn es gilt .
- Die Wahrscheinlichkeit, dass eine zufällig gewählte Zahl eine gerade (oder ungerade) Anzahl an Primfaktoren besitzt, beträgt asymptotisch , und für die summatorische Funktion der Liouville-Funktion gilt die vom zentralen Grenzwertsatz zu erwartende Schranke mit beliebigem .
- Es ist der Ausdruck unter unverändert. Ebenso bleibt die kritische Gerade (als einzige Gerade) unter unverändert.[Anm. 3]
- Alle nichttrivialen Nullstellen der Riemannschen Zeta-Funktion haben den Realteil .
In seinem, von Fields-Medaillen-Träger Peter Scholze und Jakob Stix kritisierten,[52] Beweisversuch der abc-Vermutung zieht Shin’ichi Mochizuki eine Verbindung zwischen der Riemannhypothese und anderen Theorien, darunter seiner selbst entwickelten Interuniversellen Teichmüller-Theorie und Hodge-Arakelov-Theorie aus der algebraischen Geometrie. Laut Mochizuki seien
- das Gaußsche Fehlerintegral,
- die schema-theoretische Hodge-Arakelov-Theorie,
- die Interuniverselle Teichmüller-Theorie,
- die Riemannsche Vermutung
sämtlich „Phänomene des Gewichts “ (phenomena of weight ) und, auf einer konkreten Ebene, Phänomene, die sich „um arithmetische Versionen von “ drehen.[53]
Bedeutung Bearbeiten
Primzahlen und zahlentheoretische Funktionen Bearbeiten
Restgliedabschätzungen Bearbeiten
Zahlreiche Schätzungen für zahlentheoretische Größen können im Falle der Richtigkeit der Riemannschen Vermutung bewiesen bzw. verbessert werden. Aus der Riemannschen Vermutung folgt beispielsweise eine Restgliedabschätzung im Primzahlsatz (Helge von Koch 1901):[54]
Ähnlich verhält es sich mit der Tschebyschow-Funktion . Trifft die Riemannhypothese zu, so gilt
und umgekehrt. Der minimale Abstand der Nullstellen zur Geraden kontrolliert darüber hinaus exakt die Fehlergüte im Primzahlsatz. In der Tat, ist , so gilt allgemein[55]
- und
Die Richtigkeit der Riemannschen Vermutung hätte auch unmittelbare Konsequenzen für das asymptotische Wachstumsverhalten der Zeta-Funktion auf der kritischen Geraden, also die Frage nach dem Anstieg von für . So kann etwa die Lindelöfsche Vermutung, die für alle besagt, aus der Richtigkeit der Riemannhypothese gefolgert werden.[56] Für zahlentheoretische Probleme, in denen, etwa im Rahmen der Perronschen Formel die Zeta-Funktion vertikal integriert werden muss, spielt dieses Wachstum eine entscheidende Rolle.[57] Die vertikalen Integrale kodieren die Größe der Restglieder für viele Schätzverfahren, etwa im Kontext des Dirichletschen Teilerproblems. Definiert man
so kann für alle [58]
gezeigt werden, wobei ein Polynom ist, und unter Annahme der Lindelöfschen Vermutung (insbesondere also unter Annahme der Riemannhypothese), kann der Fehler für stets zu verbessert werden.[59] Allgemeiner führt die Richtigkeit der Riemannsche Vermutung, wegen der maximalen Größe des nullstellenfreien Bereichs, zu einer Verbesserung der Selberg-Delange-Methode.[60]
Riemannsches Spektrum und Fourier-Analysis Bearbeiten
Die Fourier-Analysis beschäftigt sich, grob gesprochen, mit der Zerlegung von zum Beispiel Funktionen in ihr Spektrum. Die bedeutendsten Fälle sind die des kontinuierlichen und des diskreten Spektrums. Kann eine Funktion in ein kontinuierliches Spektrum zerlegt werden, ist sie andersherum aus einem solchen aufgebaut. Sie kann (bei einer geraden Funktion ) dann in der Form
geschrieben werden, wobei die Amplituden die Intensität beschreiben, mit der die Frequenz in auftaucht. Im Falle eines diskreten Spektrums ist aus einer Summe aus Schwingungen aufgebaut der Form[61]
- .
Aus Symmetriegründen kann die Summe auch bei begonnen werden, nachdem negative Teile des Spektrums als positiv betrachtet werden. Ist die Summe endlich, handelt es sich möglicherweise um einen Mehrklang, der durch Überlagerung mehrerer „reiner“ Schwingungen aufgebaut ist. Eine entscheidende Frage ist, ob und wie es möglich ist, aus dem Verhalten von dessen Spektrum zu rekonstruieren. Das allgemeine Werkzeug hierfür ist die Fourier-Transformation, doch bei diskreten Spektren reicht die Sprache der Funktion nicht mehr aus, die Fourier-Transformation zu beschreiben. Erst unter Verwendung von Distributionen kann dies rigoros gemacht werden, indem man festlegt, dass die inverse Fourier-Transformierte der formalen Reihe die Distribution
mit ist, unter Verwendung der Delta-Distribution.[62] Dieses Prinzip bleibt auch dann erhalten, wenn die beginnende Reihe formal ist, es werden also keinerlei Konvergenzbedingungen gestellt. Anschaulich ist eine „Funktion“, die an der Stelle „unendlich groß“ ist, und ansonsten Null. In einigen Fällen können Distributionen aber als allgemeine Fourier-Reihen aufgefasst werden, besitzen also ebenfalls ein Spektrum. Barry Mazur und William Stein weisen darauf hin, dass dies zu einer Dualität zwischen den Spektra zueinander inverser Distributionen führt. Eine Veranschaulichung ist durch Abbrechen der formalen Reihen an einer oberen Schranke mit anschließendem Auffinden von „Extremstellen“ (spike values) möglich. Betrachtet man also die endliche Summe
so ist ein spike value eine Stelle , in der für unbeschränkt ist, während es an den anderen Stellen lediglich oszilliert. Solche spike values können Informationen über das Spektrum der Transformierten kodieren, und umgekehrt.[63] Ein einfaches Beispiel ist die Reihe . Diese ist nirgends konvergent, oszilliert jedoch an allen Stellen und ist für unbeschränkt. Dies weist auf ein Spektrum hin, und in der Tat hat die Reihe wiederum spike values an den Stellen , womit die Dualität erkennbar ist.
Im Falle der Primzahlen führt eine derartige „Spektralanalyse“ über die Mangoldt-Funktion zu der formalen Reihe
womit das zu Beginn betrachtete Spektrum genau die Logarithmen aller Primpotenzen umfasst, also usw. Nach Abbruch der oberen Reihe an hohen Schranken werden zunehmend spike values erkennbar an den Stellen (siehe auch unteres, rechtes Bild)[64]
Die Werte werden auch als „Riemannsches Spektrum“ (Riemann spectrum) bezeichnet, und an den spike values der allgemeinen Fourier-Reihe
kann die Verteilung der Primzahlen exakt abgelesen bzw. rekonstruiert werden.[65] Trifft die Riemannsche Vermutung zu, so ordnen sich diese Werte auf natürliche Weise als die positiven Imaginärteile der nichttrivialen Nullstellen der Zeta-Funktion an.
-
Schaubild der Funktion mit den ersten 1000 Elementen des Riemannspektrums im Intervall . Deutlich zu erkennen sind die spike values an Primzahlpotenzen (durch die Wahl ).
-
Schaubild der Funktion . Zur Verdeutlichung sind die ersten Werte des Riemannschen Spektrums, hier ungefähr als Gipfel der spike values zu erkennen, mit roten Pfeilen markiert. Das Riemannsche Spektrum steht in einer Dualität zu den logarithmierten Primzahlpotenzen.
Terence Tao folgend sind die Primzahlen unregelmäßig über die ganzen Zahlen verteilt; wenn man jedoch eine Spektralanalyse dieser Verteilung durchführt, kann man bestimmte langfristige Oszillationen in der Verteilung erkennen (manchmal auch als die „Musik der Primzahlen“ bezeichnet), deren Häufigkeit durch eine Folge komplexer Zahlen beschrieben wird – den nichttrivialen Nullstellen der Riemannschen Zeta-Funktion. Im Prinzip sagen diese Zahlen „alles, was wir über die Primzahlen wissen wollen“.[66] Nach einem Hinweis von Andrew Granville können diese Ideen unter Annahme der Riemannhypothese mittels Techniken der Funktionentheorie, etwa Kurvenintegration, rigoros gemacht werden.[67]
Explizite Formeln Bearbeiten
Mit Hilfe der Nullstellen der Zeta-Funktion können Verteilungsfunktionen zu den Primzahlen rekonstruiert werden. Die Herleitung dieser Formeln beruht letztlich auf Methoden verwandt zur Fourier-Analysis. Ausgangspunkt sind die Perronschen Formeln. Diese besagen in ihrer effektiven Form
für und . Das bedeutet, dass eine diskrete Summe mit auf der einen Seite bis auf einen kalkulierbaren Fehler durch einen Integralausdruck auf der anderen Seite dargestellt wird. Der Integralausdruck ist ein analytischer Term, und für dessen Studium kann man sich der Eigenschaften des inneren Terms, des Integranden, bemächtigen. Durch eine Verschiebung der Integrationslinie nach links kann unter Anwendung des Residuensatzes der Funktionentheorie diese Formel expliziter gemacht werden. Dabei werden die Polstellen des Ausdrucks berücksichtigt. Polstellen entstehen unter anderem dort, wo verschwindet. Das Untermauert die Bedeutung der Nullstellen von beim Studium des Terms . Bereits Hans von Mangoldt war es möglich, die exakte, für und gültige Formel
zu beweisen, wobei die Summe über alle nichttrivialen Nullstellen von läuft. In diesem Ausdruck wird die Dualität zwischen Primzahlen und Nullstellen sichtbar. Der Term auf der rechten Seite nähert für immer genauer an, und man kann sich die Nullstellen wegen der Eulerschen Formel
als Frequenzen vorstellen, deren Überlagerung gerade die Zählfunktion ergibt. Da die Größenordnung des Terms auf der rechten Seite im Wesentlichen nur von den reellen Potenzen von bestimmt wird, reicht es für den Primzahlsatz, also , zu zeigen, dass für alle nichttrivialen Nullstellen gilt.[68] Gilt sogar für alle , also die Riemannsche Vermutung, so ist im Wesentlichen von der Ordnung einer Quadratwurzel.
Primzahlverteilung und -abstände Bearbeiten
Eine Frage der Zahlentheorie ist, wie sich die Abstände der Primzahlen verhalten, also die Differenzen , wenn die -te Primzahl bezeichnet. Zwar liefert die Riemannhypothese keine exakte Antwort auf diese Frage, dennoch sagt sie aus, dass sich die Abstände gleichmäßig durch eine verhältnismäßig „kleine“ Größe nach oben abschätzen lassen. So gilt, unter Annahme der Riemannhypothese für alle [69]
Das bedeutet, dass die Abstände zwischen zwei benachbarten Primzahlen im Wesentlichen nicht größer sind als die Quadratwurzel der kleineren Primzahl. Zum Beispiel ist
und . Jedoch können ähnliche Resultate bereits durch schwächere Annahmen erzielt werden, in etwa wenn gezeigt werden kann, dass in gewissen Teilstreifen nahe nur noch „wenige“ Nullstellen liegen können. Definiert man präzise
so kann die sog. Dichtehypothese
mit festem in manchen Fällen die Riemannsche Vermutung ersetzen.[70] So gilt unter Annahme von , , sowie für bereits
für und , mit der Tschebyschow-Funktion . Mit ist das Ergebnis nur unwesentlich schwächer als unter Annahme der Riemannschen Vermutung.[71] Die Dichteabschätzung stammt von Albert Ingham, womit sich schon zeigen lässt, dass jedes Intervall mit beliebigem eine Primzahl enthält.[72] Eine Verbesserung dieses Resultats lieferte Martin Huxley.[73]
Hinsichtlich der Verteilung von Primzahlen in „kurzen Intervallen“ weist Terence Tao darauf hin, dass die von ihm so genannte square root barrier (deutsch: „Quadratwurzelhürde“) eine feine Abschätzung verhindere. Hintergrund ist, dass im Primzahlsatz der Fehlerterm nicht unterhalb einer Quadratwurzel gedrückt werden kann. Ein starkes Beispiel dafür ist der Versuch, die größte Lücke zwischen aufeinanderfolgenden Primzahlen in einem Intervall für zu bestimmen. Es gebe, so Tao, überzeugende Heuristiken, die nahelegen, dass diese größte Lücke die Größe hat (Cramérsche Vermutung). Aber selbst wenn man die Riemannsche Vermutung annimmt, ist die beste obere Schranke für diese Lücke nur , hauptsächlich wegen der square root barrier.[74] Ferner kann die Legendresche Vermutung, die besagt, dass zwischen zwei benachbarten Quadratzahlen stets eine Primzahl liegt, selbst unter Annahme der Riemannhypothese nicht ohne Weiteres bewiesen werden.
Bezüglich der Forschung zu Primzahllücken hat sich die Siebtheorie als eine gute Alternative zur Riemannschen Vermutung erwiesen. Fortschritte in dieser Richtung stammen von Daniel Goldston, Cem Yıldırım, János Pintz sowie Yitang Zhang und James Maynard.[75][76][77][78] In etwa ist der Satz von Bombieri und Winogradow im Sinne einer Bildung von Durchschnitten über Dirichlet-Charaktere ähnlich mächtig wie die verallgemeinerte Riemannsche Vermutung.[79] Mit seiner Hilfe konnte unter anderem der Satz von Chen bewiesen werden, der besagt, dass jede hinreichend große gerade Zahl Summe einer Primzahl und einer Zahl mit maximal zwei Primfaktoren ist.
Kryptographie und Primzahltests Bearbeiten
Neben zahlreichen Anwendungen in vielen Bereichen der Mathematik ist die Riemannsche Vermutung auch in der Kryptographie von Interesse. Das RSA-Kryptosystem beispielsweise verwendet große Primzahlen, um sowohl einen öffentlichen als auch einen privaten Schlüssel zu konstruieren. Seine Sicherheit beruht auf der Tatsache, dass es für herkömmliche Computer noch keinen effizienten Algorithmus gibt, um eine Zahl in ihre Primfaktoren zu zerlegen. Die Theorie hinter RSA erfordert nur Ergebnisse aus der elementaren Zahlentheorie.[80] Wiederum auf der Grundlage der einfachen Zahlentheorie und unter Verwendung von Fermats kleinem Satz entwickelte Miller 1976 einen deterministischen Primzahltest, der unter der Annahme der so genannten verallgemeinerten Riemannschen Vermutung funktioniert.[81] Im Jahr 1980 nutzte Michael O. Rabin Millers Ergebnisse, um einen probabilistischen Test zu entwickeln, der unabhängig von der verallgemeinerten Riemannhypothese funktioniert.[82] Durch die Arbeit von Bach im Jahr 1990 kann dieser so genannte Miller-Rabin-Test in einen deterministischen Test umgewandelt werden, der mit der Geschwindigkeit abläuft, wobei wiederum die verallgemeinerte Riemannsche Vermutung vorausgesetzt wird.[83]
Montgomerys Paar-Korrelation-Vermutung Bearbeiten
Die Paar-Korrelation-Vermutung, aufgestellt von Hugh Montgomery, trifft eine Aussage über die Verteilung der Abstände zwischen benachbarten nicht-trivialen Nullstellen. Diese Fragestellung macht nur dann Sinn, wenn die Nullstellen auch alle auf einer gemeinsamen Geraden liegen. Montgomery nimmt die Riemannhypothese an und beweist damit
Weiter vermutete er
mit und falls und 0 sonst. Trifft diese zu, sind fast alle Nullstellen der Zeta-Funktion einfach, es kann im oberen Satz also durch ersetzt werden.[84]
Physik Bearbeiten
Hamiltonoperatoren und Zufallsmatrizen Bearbeiten
Eine zentrale Frage der Mathematik, aber auch der Physik, ist die Folgende: Wird ein System betrachtet, innerhalb dessen die Beobachtungen
gemacht werden, gibt es eine Möglichkeit zu beschreiben, wie diese genau verteilt bzw. angeordnet sind? Bei den Messungen könnte es sich zum Beispiel mathematisch um die Primzahlen, die positiven Imaginärteile nichttrivialer Nullstellen der Zeta-Funktion oder physikalisch die Energieniveaus von Atomkernen handeln. Hätte man ein vollumfängliches Verständnis des zugrunde liegenden Systems, so sollte es möglich sein, die Abstände exakt zu bestimmen. In der Praxis wird jedoch versucht, von der Kenntnis der Abstände zwischen den Werten zu Aussagen über das Systems zu gelangen.[85]
Der mögliche Zusammenhang zwischen den Primzahlen und Phänomenen der theoretischen Physik kann über Fragen der klassischen Mechanik motiviert werden. In etwa ist es stets möglich, eine geschlossene Lösung für das Zweikörperproblem anzugeben, das Folgendes fragt:
- Befinden sich zwei Objekte mit Massen und und Startgeschwindigkeiten bzw. an den initialen Punkten und , wie wird sich das System über die Zeit hinweg entwickeln, sofern die einzig relevante Kraft die Gravitation ist?
Bereits im Falle des Dreikörperproblems, also drei Startobjekten, ist eine geschlossene Lösung nur noch in sehr wenigen Spezialfällen zu ermitteln, das allgemeine Problem ist offen. Aus physikalischer Sicht ist geklärt, dass es eine Lösung geben muss, doch diese ist außer Reichweite, und für Probleme mit mehr als drei Objekten wie unser Sonnensystem wird es immer schwieriger. So ist es beispielsweise bis heute nicht möglich, vorherzusagen, ob der Zwergplanet Pluto nach etlichen Jahren dem gravitativen Einfluss der Sonne entweichen wird.[86]
Deutlich anspruchsvoller wird es jedoch beim Verständnisversuch zum Beispiel schwerer Atomkerne. Der Kern eines Atoms des Elementes Uran hat zum Beispiel insgesamt mehr als 200 Protonen und Neutronen, die allesamt zu einem komplexen Geflecht aus Kräften beitragen. Hätte man umfassenden Einblick in das System, das den Kern beschreibt, so ließen sich etwa dessen Energieniveaus exakt bestimmen. Durch Beschießen schwerer Atomkerne mit Neutronen konnten Resultate in diese Richtung experimentell erzielt werden, doch von einer vollständigen Analyse ist die heutige Physik noch weit entfernt. Jedoch steht eine Methode zur Formulierung solcher Probleme über sog. Operatoren auf Hilberträumen zur Verfügung. Ein Hilbertraum ist ein linearer Raum, besteht also aus Vektoren wie der klassische euklidische Raum , nur dass er unendlichdimensional ist. Beispiele von Hilberträumen sind Funktionenräume; etwa können zwei stetige Funktionen wie zwei Vektoren „mit Einträgen f(x) bzw. g(x)“ zu addiert werden, womit sich ein Vektor „mit Einträgen f(x)+g(x)“ ergibt. Ein System kann nun über eine fundamentale Gleichung der Form
beschrieben werden, wobei ein vom System abhängiger Hamilton-Operator und Energie-Eigenfunktionen mit Eigenwerten bezeichnen. Im Falle der Atomphysik ist der Operator bis heute bei Weitem zu kompliziert, um gelöst zu werden, jedoch kann das Problem durch statistische Mechanik angegangen werden. Veranschaulicht nutzt dieser Ansatz eine Form der Mittelwertbildung bei der Betrachtung sehr vieler möglicher Zustände von verschiedenen Teilchen innerhalb eines Raums. Der Physiker Eugene Paul Wigner konnte dieses Prinzip auch auf schwere Atomkerne übertragen und betrachtete anstelle eines Operators , dessen Einträge den exakten physikalischen Gesetzen entsprechen, Familien von -Matrizen, deren unabhängige Einträge durch eine Wahrscheinlichkeitsverteilung bestimmt werden. Die Statistik der Eigenwerte dieser endlichen Zufallsmatrizen kann berechnet werden, und die Durchschnitte all dieser Matrizen sollten für gegen ein „gutes Modell“ für die Energieniveaus von schweren Atomkernen streben.[87]
Schon David Hilbert und George Polya war aufgefallen, dass die Riemannhypothese folgen würde, falls die Nullstellen Eigenwerte eines Operators wären, wobei ein hermitescher (das heißt selbstadjungierter) Operator ist, der also nur reelle Eigenwerte hat, ähnlich wie die Hamiltonoperatoren in der Quantenmechanik. Nimmt man an, dass alle nichttrivialen Nullstellen auf einer Geraden liegen, können diese entsprechend dem Imaginärteil sinnvoll aneinander gereiht, und anschließend ihre Abstände untersucht werden. Im Jahr 1972 entdeckte Hugh Montgomery bei einem Gespräch mit dem Physiker Freeman Dyson, dass die Abstände von Nullstellen und von Eigenwerten zu hermiteschen Zufallsmatrizen Ähnlichkeiten aufweisen. Diese Matrizen sind dabei Teil des GUE (Gaussian unitary ensamble), die Einträge (wegen der Symmetrie gibt es dabei nur Freiheitsgrade) werden dabei unabhängig normalverteilt gewählt.[88]
In den 1990er Jahren begannen dann auch Physiker wie Michael Berry nach einem solchen zugrunde liegenden System zu suchen, etwa in der Theorie des Quantenchaos. Weitere Unterstützung finden diese Überlegungen in einer Analogie der „expliziten Formeln“ in der Theorie der Riemannschen Zeta-Funktion mit der Selberg-Spurformel, die die Eigenwerte des Laplace-Beltrami-Operators auf einer Riemannfläche mit den Längen der geschlossenen Geodäten in Beziehung setzt, und der Gutzwiller-Spurformel in der Quantenchaos-Theorie. Diese verbindet die Eigenwerte (Energien) der quantenmechanischen Version eines chaotischen klassischen Systems mit den Längen der periodischen Bahnen im klassischen Fall. Bei all diesen Spurformeln handelt es sich um Identitäten zwischen den Summen der jeweiligen Nullstellen, Bahnkurven-Periodenlängen, Eigenwerte usw.
Statistische Mechanik Bearbeiten
Eine weitere Idee aus der Physik, die in Zusammenhang mit der Riemannschen Vermutung diskutiert wurde, sind die „Yang-Lee-Nullstellen“ der ins Komplexe analytisch fortgesetzten Zustandssumme in Modellen der statistischen Mechanik. Chen Ning Yang und Tsung-Dao Lee bewiesen unter Verwendung eines Resultats von George Polya aus der Theorie der Zeta-Funktion, auf das sie Mark Kac aufmerksam machte,[89] dass in bestimmten Modellen die Nullstellen auf einem Kreis liegen, bei anderen Modellen nach einem Variablenwechsel liegen sie auf einer Geraden.[90] Es existieren Ansätze, dieses Resultat der statistischen Mechanik auf die Zeta-Funktion zu übertragen.[91]
All diesen Ideen liegt eine Analogie zugrunde, die sich vereinfacht etwa so beschreiben lässt: Die Primzahlen sind „Elementarteilchen“, die über die Multiplikation in Wechselwirkung treten und so die zusammengesetzten Zahlen aufbauen. Gleichzeitig werden die „Teilchen“ durch die Addition angeordnet. In der Zeta-Funktion werden nun in Form einer Summen- bzw. Produktformel beide Aspekte (additiv / natürliche Zahlen und multiplikativ/Primzahlen) miteinander verbunden.
Quasikristalle Bearbeiten
Eine Verbindung der Riemannschen Vermutung zu eindimensionalen Quasikristallen schlug Freeman Dyson 2009 vor.[92] Die mathematische Definition eines Quasikristalls lautet wie folgt. Ein Quasikristall ist eine Verteilung von diskreten Punktmassen, deren Fourier-Transformation eine Verteilung von diskreten Punktfrequenzen ist. Kurz gesagt, ein Quasikristall ist eine reine Punktverteilung, die ein reines Punktspektrum hat. Diese Definition schließt als Sonderfall die gewöhnlichen Kristalle ein, die exakt periodische Punktverteilungen mit exakt periodischen Punktspektren sind. Wenn die Riemannhypothese wahr ist, dann bilden, so Dyson, die Nullstellen der Zeta-Funktion gemäß der Definition einen eindimensionalen Quasikristall. Sie bilden eine Verteilung von Punktmassen auf einer Geraden, und ihre Fourier-Transformierte ist ebenfalls eine Verteilung von Punktmassen, jeweils eine bei den Logarithmen der gewöhnlichen Primzahlen. Dyson schlägt nun einen Ansatz vor, der die eindimensionalen Quasikristalle sämtlich klassifizieren und in deren Auflistung einen finden soll, der sich mit den Nullstellen der Zeta-Funktion identifizieren lässt.[93]
Geschichte Bearbeiten
Riemanns Originalarbeit von 1859 Bearbeiten

Im Jahr 1859 verfasste Bernhard Riemann, als Dank für seine Aufnahme in die Berliner Akademie der Wissenschaften, eine insgesamt 9-seitige Schrift, die später die Grundlagen für die moderne analytische Zahlentheorie legen sollte. Seine Arbeit zielte darauf ab, die Vermutung von Gauß zum Primzahlsatz zu beweisen und weiter zu vertiefen. Da der Aufsatz jedoch äußerst skizzenhaft aufgeführt war und zahlreiche darin getätigte Aussagen nicht streng bewiesen wurden, sollte es noch dauern, bis die Mathematiker die dort getätigten Behauptungen akzeptierten. Alle Aussagen Riemanns in seiner Arbeit, mit Ausnahme der dort in einem Nebensatz formulierten Riemannschen Vermutung und seiner Behauptung für die Häufigkeit der Nullstellen auf der kritischen Geraden, die jedoch aus der Riemannschen Vermutung folgen würde, gelten als bewiesen.
Die Riemannsche Vermutung wurde durch Riemann nebensächlich erwähnt, und nicht explizit als wichtiges Problem ausgewiesen. Riemann selbst schreibt über die Nullstellen der von ihm definierten Xi-Funktion:
„Man findet nun in der That etwa so viel reelle Wurzeln innerhalb dieser Grenzen, und es ist sehr wahrscheinlich, daß alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indeß die Aufsuchung desselben, nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien.“[94]
Er sicherte seine Vermutung jedoch durch aufwändige handschriftliche Berechnungen einiger weniger Nullstellen ab, wie Carl Ludwig Siegel in den 1930er Jahren bei der Untersuchung von Riemanns Nachlass herausfand.[95] In seinen nicht veröffentlichten Schriften wurde darüber hinaus nichts dazu gefunden.[96]
Trotz ihrer bahnbrechenden Wirkung verblieb Über die Anzahl der Primzahlen unter einer gegebenen Grösse der einzige Beitrag Riemanns zur Zahlentheorie. Der Schwerpunkt seiner Forschung lag in der Geometrie, sowie der Funktionentheorie, und deren Synthese. So entwickelte er das Konzept der Riemannschen Fläche und bewies den Riemannschen Abbildungssatz. Auch tat er sich als Pionier der modernen Differentialgeometrie hervor, wo er unter anderem das Konzept der Riemannschen Metrik etablierte, das unter anderem wichtig für die allgemeine Relativitätstheorie ist. Es definiert einen (lokalen) Abstandsbegriff auf gekrümmten Flächen bzw. Figuren. Riemann verstarb im Alter von nur 39 Jahren an den Folgen einer Tuberkulose.
Der Mathematiker und Mathematikhistoriker Harold Edwards formuliert einige Spekulationen, wie Riemann ohne nennenswerte numerische Evidenz zu seiner Vermutung gekommen sein könnte.[97] Präziser liefert Edwards einen Erklärungsversuch, was Riemann zu der Formulierung „sehr wahrscheinlich“ veranlasste. Als zentral wird die Rolle der Riemann-Siegelschen Theta-Funktion gesehen. Mit Hilfe dieser Funktion lässt sich die Anzahl der Nullstellen der Zeta-Funktion im Bereich berechnen.[98][99] Es gilt die Näherung
und Edwards argumentiert, dass Riemann heuristisch geschlossen haben könnte, dass der Term gleichzeitig die ungefähre Anzahl der Nullstellen beschreibt, die auf der kritischen Geraden liegen, also die Vermutung erfüllen.[100]
Im 20. Jahrhundert Bearbeiten
Hilberts achtes Problem Bearbeiten

Im Rahmen des 2. Internationalen Mathematikerkongresses des Jahres 1900 in Paris hielt David Hilbert am 8. August einen Vortrag. In diesem formulierte er eine Liste von 23 mathematischen Problemen, die seiner Ansicht nach zu den wichtigsten des kommenden Jahrhunderts zählten. Hilbert gehörte zu diesem Zeitpunkt bereits zu den führenden Mathematikern der Gegenwart. Problem Nr. 8 war die Riemannsche Vermutung:
„In der Theorie der Verteilung der Primzahlen sind in neuerer Zeit durch Hadamard, De La Vallee-Poussin, V. Mangoldt und andere wesentliche Fortschritte gemacht worden. Zur vollständigen Lösung der Probleme, die uns die Riemannsche Abhandlung „Über die Anzahl der Primzahlen unter einer gegebenen Größe“ gestellt hat, ist es jedoch noch nötig, die Richtigkeit der äußerst wichtigen Behauptung von Riemann nachzuweisen, daß die Nullstellen der Funktion , die durch die Reihe dargestellt wird, sämtliche den reellen Bestandteil haben – wenn man von den bekannten negativ ganzzahligen Nullstellen absieht. Sobald dieser Nachweis gelungen ist, so würde die weitere Aufgabe darin bestehen, die Riemannsche unendliche Reihe für die Anzahl der Primzahlen genauer zu prüfen und insbesondere zu entscheiden, ob die Differenz zwischen der Anzahl der Primzahlen unterhalb einer Größe und dem Integrallogarithmus von in der Tat von nicht höherer als der ten Ordnung in unendlich wird, und ferner, ob dann die von den ersten komplexen Nullstellen der Funktion abhängenden Glieder der Riemannschen Formel wirklich die stellenweise Verdichtung der Primzahlen bedingen, die man bei den Zählungen der Primzahlen bemerkt hat.“
Hilbert selbst ordnete die Riemannsche Vermutung als weniger schwierig ein als beispielsweise das Fermat-Problem: In einem Vortrag 1919 gab er der Hoffnung Ausdruck, dass ein Beweis noch zu seinen Lebzeiten gefunden würde, im Fall der Fermat-Vermutung vielleicht zu Lebzeiten der jüngsten Zuhörer; für am schwierigsten hielt er die Transzendenz-Beweise in seiner Problemliste[102] – ein Problem, das in den 1930er Jahren durch Gelfond und Theodor Schneider gelöst wurde.[103] Das Fermat-Problem wurde im Jahr 1995 von Andrew Wiles und Richard Taylor im Rahmen ihres Beweises des Modularitätssatzes gelöst.
Das hohe Ansehen, das Hilbert genoss, beflügelte die Mathematiker, sich mit seinen Problemen, darunter der Zeta-Funktion, auseinanderzusetzen. Bis heute gelten 15 der 23 Probleme als gelöst, jedoch nicht die Riemannsche Vermutung.[104]
Einflüsse auf die Zahlentheorie in England Bearbeiten

Der berühmte britische Mathematiker Godfrey Harold Hardy pflegte vor der Überquerung des Ärmelkanals bei schlechtem Wetter ein Telegramm abzuschicken, in dem er behauptete, einen Beweis gefunden zu haben, dem Beispiel von Fermat folgend, der auf dem Rand eines Buches der Nachwelt überlieferte, er hätte für seine Vermutung einen Beweis, der leider zu lang sei um auf dem Rand Platz zu finden.[105] Sein Kollege John Edensor Littlewood bekam in Cambridge 1906 als Student sogar die Riemannhypothese als funktionentheoretisches Problem von seinem Professor Ernest William Barnes gestellt, ohne Verbindung zur Primzahlverteilung – diesen Zusammenhang musste Littlewood für sich entdecken und bewies in seiner Fellowship-Dissertation, dass der Primzahlsatz aus der Hypothese folgt, was aber in Kontinentaleuropa schon länger bekannt war. Wie er in seinem Buch A mathematician’s miscellany zugab, warf dies kein gutes Licht auf den damaligen Stand der Mathematik in England. Littlewood leistete aber bald darauf wichtige Beiträge zur analytischen Zahlentheorie im Zusammenhang mit der Riemannhypothese.[106]
Aufnahme in die Liste der Smale-Probleme Bearbeiten
Stephen Smale, Träger der Fields-Medaille, veröffentlichte 1998 seine eigene – im Sinne von Hilbert verfasste – Liste von 18 Problemen. Problem Nummer 1 ist die Riemannsche Vermutung. Bisher wurden nur wenige Probleme auf Smales Liste gelöst.
Im 21. Jahrhundert: Erklärung zum Millennium-Problem Bearbeiten

Bereits im Jahr 1998 wurde das Clay Mathematics Institute (CMI) durch den Geschäftsmann Landon T. Clay und den Mathematiker Arthur Jaffe gegründet,[107] wobei Jaffe von 1998 bis 2011 auch die erste Präsidentschaft innehatte. Das CMI feierte das einhundertste Jahr nach Hilberts Rede auf dem Pariser Kongress im Jahr 1900 durch eine zweitägige Konferenz am Collège de France im Mai 2000. Dabei wurde ein 7-Millionen-Dollar-Fonds vorgestellt, von dem jeweils 1 Million Dollar für die Lösung von sieben großen mathematischen Problemen vergeben wird, den sogenannten Millennium-Problemen.[108] Die Preise wurden schließlich im Juni bekanntgegeben nach Angaben des CMI ins Leben gerufen, um
- einige der wohl schwierigsten Probleme zu würdigen, mit denen Mathematiker um die Jahrtausendwende zu kämpfen hatten,
- die Bedeutung der Arbeit an den wirklich schwierigen Problemen zu unterstreichen und
- bekannter zu machen, dass es in der Mathematik immer noch schwierige, bedeutende Probleme gibt.[109]
Da im 20. Jahrhundert kein Beweis für die Riemannsche Vermutung gefunden wurde, ist dieses Vorhaben zu einem der Millennium-Probleme erklärt worden. Dabei hatte es in der Liste die Position 4 erhalten, wobei sich die Rangfolge aber lediglich durch die Länge der Problemnamen definierte.[108]
Damit das Preisgeld verliehen werden kann, muss die betroffene Arbeit publiziert worden sein, und nach einer Ruhefrist von 2 Jahren von der Mathematikergemeinschaft eine breite Akzeptanz erfahren haben.[110] Unter den Regeln der Preisverleihung findet sich ferner auch eine Klausel bezüglich der Rolle von Gegenbeispielen. Im Falle der Riemannhypothese wäre ein Gegenbeispiel eine nichttriviale Nullstelle, die nicht auf der kritischen Geraden liegt, und eine solche könnte auch ohne tiefere Einsichten über die Problematik durch langes Rechnen mittels eines Computers entdeckt werden. Wenn nach Ansicht des CMI das Gegenbeispiel das Problem tatsächlich löst, könne das CMI die Verleihung des Hauptpreises aussprechen. Zeige hingegen das Gegenbeispiel, dass das ursprüngliche Problem nach Umformulierung oder Eliminierung eines Spezialfalls weiterbesteht, könne das CMI dem Autor lediglich einen kleinen Preis verleihen, dessen Höhe CMI nach eigenem Ermessen festlegt. Das Geld für diesen Preis werde dann nicht aus dem Problemfonds, sondern aus anderen CMI-Fonds entnommen.[111]
Forschungsgeschichte Bearbeiten
Beweis- und Widerlegungsversuche bedeutender Mathematiker Bearbeiten
Wegen ihrer enormen Bedeutung haben sich zahlreiche Forscher bereits an einem Beweis oder einer Widerlegung der Riemannhypothese versucht. Der Mathematiker Ken Ono meint, dass es „schwierig sei“, alle unternommenen Versuche zu zählen, und schätzt, dass es bisher „hunderte“ sind. Bislang habe jedoch keiner der Beweisversuche einer Überprüfung standgehalten, und für einen erfolgreichen Beweis sei eine „ganz andere Ebene der Mathematik“ vonnöten.[112] Unter einigen wenig bekannten Mathematikern und Amateuren gab es im Laufe der Zeit auch Vorstöße von bedeutenden Forschern, von denen einige im Folgenden angeführt sind.
Thomas Jean Stieltjes (1885–1894) Bearbeiten

Im Jahr 1885 unternahm Thomas Jean Stieltjes einen ersten Lösungsversuch.[113] Er behauptete, dass die Reihe für alle reellen Werte konvergiert. In einem Brief an Charles Hermite schrieb er:
„J’ai été … assez heureux … en demontrant cette propriété annoncée comme trés probable par Riemann, que toutes raciness de sont réelles. … Mais toutes ces recherches demanseront encore beaucoup de temps … Comme je ne puis pas pousser, en ce moment, activemenr ce travail à cause d’autres devoirs, je me propose de prendre un peu haleine et de laisser tout cela pendant quelques mois. Mais il n’y aura pas d’inconvénient, je l’esspére a publier dans les Comptes Rendus la Note ci-jointe qui, me semble, doit intéresser les géometres qui ont étudie le Mémoire de Riemann.“
„Ich war … ziemlich glücklich … als ich die von Riemann als sehr wahrscheinlich angekündigte Eigenschaft bewies, dass alle Wurzeln von reell sind. … Aber all diese Forschungen werden trotzdem noch viel Zeit in Anspruch nehmen … Da ich im Moment wegen anderer Aufgaben nicht in der Lage bin, diese Arbeit aktiv voranzutreiben, nehme ich mir vor, ein wenig durchzuatmen und alles für ein paar Monate ruhen zu lassen. Ich hoffe, dass es keine Unannehmlichkeiten gibt, wenn ich die beigefügte Notiz in den Comptes Rendus veröffentlichen werde, da ich glaube, dass diese Frage für die Geometer, die Riemanns Memoiren studiert haben, von Interesse sein sollte.“

Als Hermite in einer Antwort nach mehr Details fragte, gab Stieltjes in einem weiteren Brief vom 11. Juli 1885 weitere Ausführungen, die auf einer Ungleichung des Typs
mit einer festen Konstanten basierten, wobei die Mertensfunktion bezeichnet. Eine entsprechende Behauptung hatte er schließlich 1885 in seinem Aufsatz im Comptes Rendus der Académie des sciences aufgestellt.[115] Jedoch gab Stieltjes keinerlei Hinweis darauf, wie er zu dieser Ungleichung gelangt war, und schrieb stattdessen nur:
„Ma demonstration est bien pénible; je tâcherai, lorsque je reprendrai ces recherches, de la simplifier encore.“
„Mein Beweis ist ziemlich mühsam; wenn ich auf diese Untersuchungen zurückkomme, werde ich versuchen, sie zu vereinfachen.“
Auch in einem späteren Brief an Magnus Gösta Mittag-Leffler blieb er wenig konkret und nannte den Beweis des Lemmas „rein arithmetisch“ und „sehr schwierig“. Er habe das Ergebnis aus einer Reihe vorangegangener Aussagen erhalten, sei jedoch in der bereits 1885 vorgenommenen Vereinfachung nicht weiter gekommen.[114] Zur gleichen Zeit skizzierte Stieltjes die Schlussfolgerung des Primzahlsatzes aus seiner behaupteten Ungleichung für die Mertensfunktion in der sehr starken Form
für jedes . Zuvor hatte er sogar den besseren Fehlerterm angekündigt, seine Behauptung in einem weiteren Brief an Mittag-Leffler vom 23. März 1887 jedoch wieder zurückgenommen. Später war Stieltjes immer noch von der Richtigkeit seines Beweises überzeugt, wie weitere Briefe an Mittag-Leffler und auch Hermite aus den Jahren 1887 bzw. 1891 belegen. Er starb schließlich Ende des Jahres 1894 im Alter von nur 38 Jahren, und sein angeblicher Beweis wurde nie veröffentlicht. Zum Beispiel verkündete Jacques Hadamard 1896 ohne nähere Ausführungen in seiner Arbeit Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques[116] in der er den Primzahlsatz bewies, dass der kürzlich verstorbene Stieltjes die Riemannsche Vermutung bewiesen habe, ohne den Beweis zu publizieren. Laut Simon Cornelis van Veen, Professor für Mathematik an der Universität Leiden, an der zuvor auch Stieltjes wirkte, fanden sich in Stieltjes Nachlass keinerlei Spuren eines Beweises.[117]
Aus heutiger Perspektive wird es als sehr unwahrscheinlich eingeschätzt, dass Stieltjes über einen korrekten Beweis der Riemannhypothese verfügte. Zwar gehörte er zu den ersten Mathematikern, die offene Fragen in Riemanns revolutionärer Arbeit ergründeten, jedoch sei nach Aussage von Harold Edwards in der Vergangenheit hinreichend viel über die Riemannhypothese gearbeitet worden, dass man jedem angeblichen Beweis „zurecht mit großer Skepsis gegenüberstehe“. Unterstrichen werde dies durch die Unfähigkeit Stieltjes, seinen Beweis auch in späteren Jahren wiedergegeben zu haben. Zudem ist, selbst unter Annahme der Riemannschen Vermutung, bis heute die Frage offen, ob überhaupt gilt.[118] Es könnte bis dato lediglich
gefolgert werden.[84] Der Fall , also , genannt die Mertensvermutung, konnte ferner 1985 durch aufwändigen Einsatz von Computern, mittels Berechnung der ersten 2000 nichttrivialen Nullstellen der Zeta-Funktion auf mindestens 100 Nachkommastellen, widerlegt werden. Dabei wurde eine Beziehung zwischen und den Nullstellen ausgenutzt.[119]
Alan Turing (1937–1952) Bearbeiten

Alan Turing war der Meinung, die Vermutung sei falsch. Vorausgegangen waren Gespräche zwischen Turing und Godfrey Harold Hardy 1937 in Princeton, in denen sich Hardy pessimistisch über die Richtigkeit der Riemannhypothese äußerte. Hintergrund waren die zahlreichen vergeblichen Versuche Hardys, des Problems Herr zu werden. In der Überzeugung, dass die Riemannsche Vermutung falsch sein müsste, schloss Turing, dass unter Einsatz möglichst großer Rechenleistung eine Nullstelle gefunden werden könne, die diese verletze. Turings Biograph Andrew Hodges schreibt diesbezüglich:
„Apparently he had decided that the Riemann hypothesis was probably false, if only because such great efforts had failed to prove it. Its falsity would mean that the zeta- function did take the value zero at some point which was off the special line, in which case this point could be located by brute force, just by calculating enough values of the zeta-function.“
„Offensichtlich hatte er [Turing] entschieden, dass die Riemannsche Hypothese wahrscheinlich falsch war, und sei es nur, weil so große Anstrengungen fehlgeschlagen sind, sie zu beweisen. Die Falschheit der Riemannschen Hypothese würde bedeuten, dass die Zeta-Funktion an einem Punkt, der außerhalb der speziellen Linie [kritischen Geraden] liegt, den Wert Null annimmt. In diesem Fall könnte dieser Punkt brute force gefunden werden, indem einfach genügend Werte der Zeta-Funktion berechnet werden.“
Dieses Programm war jedoch bereits in Angriff genommen worden. Tatsächlich hatte Riemann selbst die ersten Nullstellen ausfindig gemacht und überprüft, dass diese allesamt auf der kritischen Geraden lagen. In den Jahren 1935 bis 1936 hatte der Oxforder Mathematiker Edward Charles Titchmarsh mit Hilfe von Lochkarten, die damals für die Berechnung astronomischer Vorhersagen verwendet wurden, gezeigt, dass die ersten 1041 Nullstellen der Zeta-Funktion alle auf der kritischen Geraden lagen.[121] Turings Vorhaben, eine weit größere Zahl an Nullstellen zu berechnen, brachte jedoch zwei Kernprobleme mit sich. Aufgrund ihrer schwierigen Definition konnte die Riemannsche Zeta-Funktion einerseits, wenn überhaupt, nur annähernd numerisch berechnet werden. Dabei oblag den Mathematikern der Nachweis, dass die Fehlerterme bei dieser Annäherung für ein korrektes Endergebnis hinreichend klein waren. Titchmarshs Vorgehensweise hatte auf einer Methode von Riemann aufgebaut, die allerdings erst 70 Jahre später beim Aufarbeiten von Riemanns Nachlass durch Carl Ludwig Siegel bekannt wurde. Für die Ausweitung dieser Berechnungen auf tausende weitere Nullstellen bedurfte es einer Neujustierung der Methodik, besonders hinsichtlich der Fehlerabschätzungen.[122] Das zweite Problem betraf die Bewältigung der zahlreichen elementaren Rechenoperationen, die mit der Berechnung einhergingen, etwa Additionen, Multiplikationen oder auch Auswertungen trigonometrischer Funktionen bzw. massenhaftes Nachschlagen von Werten in Kosinustabellen. Dass die Berechnungsmuster jenen ähnelten, die zur Bestimmung von Planetenpositionen gebraucht wurden, war schon Titchmarsh bewusst gewesen, weshalb seine Rechnungen mit den Lochkartenmethoden der Planetenastronomie durchgeführt worden waren. Für die annähernde Bestimmung der Zeta-Werte wurden Überlagerungen von Schwingungen im großen Stil gebraucht. Turing hatte erkannt, dass der Algorithmus auch jenem zur Bestimmung der Gezeiten ähnelte, denn diese konnten als Summe einer Reihe von Wellen mit unterschiedlichen Perioden betrachtet werden: tägliche, monatliche, jährliche Schwingungen von Anstieg und Rückgang. Eine für solche Probleme konstruierte Maschine gab es damals bereits in Liverpool. Diese arbeitete nach einem völlig analogen Prinzip, wandelte also theoretische Rechnungen in explizite physikalische Vorgänge um, was im Gegensatz zur Turing-Maschine stand, die lediglich mit Symbolen hantierte. Turing erkannte, dass eine solche analoge Maschine massenhaft Additions-, Multiplikations- bzw. Nachschlageoperationen in Kosinustabellen sparen konnte.[123]
Dank des Einflusses Hardys und Titchmarshs wurde Turings Antrag auf Unterstützung des Projektes bei der Royal Society genehmigt, und sein Vorhaben mit 40 Pfund unterstützt. Im Sommer 1939 glich sein Zimmer einer „Rumpelkammer aus Zahnrädern, die überall auf dem Boden verteilt waren“.[124] Doch 1940 wurde seine Arbeit durch die Wirrungen des Zweiten Weltkrieges jäh unterbrochen. England zog alle intellektuellen Kräfte in Bletchley Park zusammen, um die deutsche Enigma-Chiffriermaschine zu knacken. Zwar konnte Turing nicht weiter nach Nullstellen suchen, doch seine Vorarbeit ließ sich überraschend gut auf die Dechiffrierarbeiten anwenden. Erst um 1950 brachte er seine ursprünglich für die Zeta-Funktion konstruierte Maschine zum Laufen, die 1104 Nullstellen berechnen konnte, eh sie zusammenbrach. Weitere Forschungen an der Riemannschen Vermutung blieben Turing jedoch verwehrt, da er 1952 wegen seiner Homosexualität verhaftet, und wegen eines „grob anzüglichen Akts“ zu einer medikamentösen Behandlung verurteilt wurde. Am 8. Juni 1954 wurde er tot in seinem Zimmer aufgefunden, wobei die Todesursache eine Cyanidvergiftung war.[125]
Hans Rademacher (1945) Bearbeiten

1945 behauptete Hans Rademacher, die Vermutung widerlegt zu haben, und erregte damit einiges Aufsehen in den USA. John Robert Kline von der University of Pennsylvania, an der auch Rademacher lehrte, hatte den Herausgeber Abraham A. Albert der Transactions of the American Mathematical Society per Telegramm informiert, dass ein erfolgreicher Widerlegungsschluss bald publiziert werden könne. Auf das Telegramm hin kam ein Brief von Rademacher selbst, in dem er mitteilte, dass seine Berechnungen von dem berühmten Mathematiker Carl Siegel vom Princeton Institute for Advanced Study überprüft und bestätigt worden waren. Herausgeber Albert machte sich bereit, die historische Arbeit bereits in der Mai-Ausgabe zu veröffentlichen. Nur eine Woche vor dem Druck der neuen Ausgabe wurde allerdings mitgeteilt, dass Siegel doch noch einen Fehler in der Argumentation von Rademacher entdeckt hatte. Albert kommentierte dies mit: „Die ganze Sache hat sicherlich eine Menge falscher Hoffnungen geweckt“.[126]
Der Denkfehler Rademachers hatte seinen Ursprung in der Mehrdeutigkeit des komplexen Logarithmus. Im Gegensatz zur Situation im Reellen gibt es keine Möglichkeit, den komplexen Logarithmus als eine überall außerhalb von 0 stetige, geschweige denn differenzierbare, Funktion in der komplexen Ebene zu begreifen. Vielmehr gibt es theoretisch unendlich viele Logarithmen eines festgelegten Wertes, und man ist zur Herstellung einer klaren Vorschrift gezwungen, sich auf einen Zweig festzulegen, wobei jedoch die Unstetigkeit entsteht. Rademacher hatte indes zwei verschiedene Zweige für Werte angenommen, die jedoch demselben gewählten Zweig zugehörig sein mussten.[127]
John Forbes Nash Jr. (1959) Bearbeiten

Der US-amerikanische Mathematiker und spätere Nobel- und Abelpreisträger John Forbes Nash war fasziniert von dem Problem. Erwiesenermaßen hatte er schon als Vierzehnjähriger in Eric Temple Bells Buch Men of Mathematics (1937) über die Riemannsche Vermutung gelesen. Bereits als junger Mann war er vom Magazin Fortune als der „vielversprechendste Mathematiker der Welt“ gekürt worden, weshalb Kollegen ihm einen Beweis zutrauten. Im Frühjahr 1959 kündigte er an, dass eine seiner Ideen, die auf der Theorie der Pseudoprimzahlen beruhte, möglicherweise funktionieren könnte. In einem Vortrag vor großem Publikum trug er schließlich seine Gedanken vor, die die versammelten Zuhörer völlig entsetzten, da, wie Donald Newman später berichtete, „kein Wort zum anderen passte“. Die Präsentation sei, so Newman, „schrecklich“ gewesen. Tatsächlich war der Vortrag eine Auswirkung von Nashs Schizophrenie, die sich seit einiger Zeit entwickelt hatte und ihn schließlich für viele Jahre arbeitsunfähig machen sollte.[128]
Hideya Matsumoto (1984) Bearbeiten
Auf einer im Jahr 1984 gehaltenen Konferenz in Paris gab der dort wirkende japanische Mathematiker Hideya Matsumoto[129] einen Vortrag über Metaplektische Gruppen. Obwohl in der Ankündigung nicht erwähnt, behauptete er in seinem Vortrag aus der Positivität einer sphärischen Funktion die Riemannhypothese folgern zu können, und außerdem, dass er die Positivität beweisen könne. Die in seinen Ausführungen skizzierten Details waren jedoch unvollständig, es gab aber ein Manuskript. Die Ankündigung erregte damals einige Aufmerksamkeit unter Mathematikern. Samuel Patterson, der dem Vortrag ebenfalls beiwohnte, nahm das ernst, da seine bisherige Arbeit (unter anderem algebraische K-Theorie) ihn als fähigen Mathematiker auswies.[130] Zur selben Zeit arbeitete Aleksandar Ivić an seinem Buch über die Riemannsche Zeta-Funktion, in dem er unter anderem den Beweis für das bis dato optimale nullstellenfreie Gebiet einarbeitete. Er konnte bei der Sichtung des angeblichen Beweises jedoch mit den ungewöhnlichen Methoden Matsumotos wenig anfangen und zeigte sich tief frustriert, da er viel Zeit in das Buch investiert hatte, und nun fürchtete, es könne noch vor seiner Veröffentlichung an Bedeutung verlieren. Wenig später fand Yōichi Motohashi, der sich auf Wunsch eines der führenden japanischen Mathematiker Kunihiko Kodaira damit befasste, beim Durchsehen des Manuskripts jedoch einen Fehler in der Definition des Logarithmus der Zeta-Funktion, der jenem von Rademacher zuvor zu ähneln schien. Auch Patterson beschäftigte sich einige Jahre mit dem Beweisversuch, erklärte ihn schließlich auch für falsch, nannte ihn jedoch den bisher „bei weitem ernsthaftesten Versuch“.[131]
Louis de Branges de Bourcia (seit 1985) Bearbeiten

Louis de Branges de Bourcia beschäftigte sich jahrzehntelang mit dem Problem. Im Jahr 1985, kurz nach seinem erfolgreichen Beweis der berühmten Bieberbach-Vermutung, stellte er einen auf seiner Theorie der Hilberträume ganzer Funktionen basierenden Beweisversuch vor. Nachdem das Manuskript nur wenig Beachtung gefunden hatte, wurde es schließlich Peter Sarnak übergeben, der damals gerade sein Mathematikstudium in der Graduate School abgeschlossen hatte. Nachdem sich Sarnak „viele Stunden“ mit dem Beweis beschäftigt hatte, fand er schließlich einen „fatalen Fehler“ (big blunder).[132] Andrew Odlyzko äußerte sich zudem skeptisch, ob der Ansatz an sich fruchtbar sei. Seiner Auffassung nach sei es „unnatürlich“, die Zeta-Funktion in solch einem allgemeinen Framework geeignet unterzubringen.[133]
Bereits 1989 präsentierte de Bourcia anlässlich einer Vortragsreihe im Institut Henri Poincaré in Paris einen weiteren Beweisversuch. Die auf 450 Minuten angesetzte Vortragsreihe in fünf Teilen wurde von der Gemeinschaft negativ aufgenommen. Kritisiert wurde, dass in den ersten viereinhalb Teilen im Wesentlichen bloß bekannte historische Tatsachen über die Vermutung zusammengetragen wurden, während für die Skizzierung des eigentlichen Beweisversuchs nur etwa eine halbe Stunde übrig blieb. Der Beweis wurde schließlich in schnellem Tempo durchgegangen, wobei sich de Bourcia auch nach dem Vortrag nicht anschickte, auf Fragen zu technischen Details genauer einzugehen. Kurz nach seiner Rückkehr in die USA erkannte er seinen neuen Beweis selbst als fehlerhaft.[134]
2004 veröffentlichte er einen neuen Beweis, der kritisch geprüft wurde. Bereits Jahre zuvor hatte Eberhard Freitag jedoch ein Gegenbeispiel für eine im Beweis aufgestellte Behauptung gegeben, sodass der Beweis mittlerweile als falsch angesehen wird.
Michael Francis Atiyah (2018) Bearbeiten

Im Jahr 2018 kündigte der Fields-Medaillen- und Abelpreisträger Michael Atiyah einen Beweis an und löste damit ein großes Medienecho aus.[135][136] Einen Vortrag über seine Beweisstrategie hielt er am 24. September 2018 im Laureate Forum in Heidelberg.[137] Zu diesem Zeitpunkt war Atiyah bereits 89 Jahre alt. Er selbst bezeichnete seinen Versuch als „einfachen Beweis“, der auf Vorarbeiten der führenden Mathematiker John von Neumann, Friedrich Hirzebruch und Paul Dirac aufbaue. Ausgeschrieben benötige er nicht mehr als 5 Seiten.[138] Durch Zusammenführen ihrer Erkenntnisse und unter der Annahme, dass die Riemannsche Vermutung nicht zutrifft, behauptete Atiyah, zu einem Widerspruch zu gelangen. „Es sieht wie ein Wunder aus“, sagte Atiyah, „aber ich behaupte, dass die ganze harte Arbeit schon vor 70 Jahren geleistet wurde“.[139]
Atiyahs Beweisversuch wurde von der Wissenschaftsgemeinschaft mit Skepsis und wenig Resonanz aufgenommen.[112][139] Ein Grund dafür ist, dass Atiyah in den letzten Jahren immer wieder fehlerhafte Beweise für einige Probleme geliefert hatte.[138] So äußerte etwa der Physiker John Baez: „Ich wette, dass Atiyahs behaupteter Beweis […] Experten nicht überzeugen wird. Im Jahr 2017 behauptete er, einen 12-seitigen Beweis für den Satz von Feit-Thompson zu haben, der normalerweise 255 Seiten umfasst. Er zeigte ihn den Experten und … Schweigen“.[140] Die Fachzeitschrift Science kontaktierte mehrere Kollegen von Atiyah. Sie alle äußerten sich „besorgt“ über seinen Wunsch, den Ruhestand zu verlassen, um Beweise zu präsentieren, die lediglich auf „wackeligen Assoziationen“ (shaky associations) basierten, und sagten, es sei „unwahrscheinlich“, dass sein Beweis der Riemannschen Vermutung erfolgreich sein würde. Laut Science wollte jedoch keiner seinen Mentor oder Kollegen öffentlich kritisieren, aus Angst, die Beziehung zu gefährden.[138] Atiyah selbst blieb durch die geäußerte Skepsis unbeeindruckt, und äußerte: „Niemand glaubt einen Beweis der Riemannhypothese, schon gar nicht einen Beweis von jemandem, der 90 Jahre alt ist“, und fügte hinzu: „Die Leute sagen: ‚Wir wissen, dass Mathematiker am besten arbeiten, bevor sie 40 sind‘. Ich versuche, ihnen zu zeigen, dass sie falsch liegen. Dass ich auch mit 90 noch etwas leisten kann“.[140]
Im Januar 2019 verstarb Michael Atiyah im Alter von 89 Jahren.
Teilresultate Bearbeiten
Nullstellen auf der kritischen Geraden Bearbeiten
Satz von Hardy Bearbeiten

Der Satz von Hardy, 1914 bewiesen durch Godfrey Harold Hardy,[141] besagt, dass unendlich viele nichttriviale Nullstellen der Riemannschen Zeta-Funktion auf der kritischen Geraden liegen. Abgesehen von numerischen Arbeiten von Jørgen Pedersen Gram und R. J. Backlund war dies das erste konkrete Resultat über die Nullstellen der Riemannschen Zeta-Funktion auf der kritischen Geraden.[142] In seinem damals revolutionären Beweis machte sich Hardy zunutze, dass für alle reellen Zahlenwerte der Ausdruck
nur reelle Funktionswerte annimmt. Dies vereinfachte das Problem auf die zu klärende Existenz unendlich vieler Nullstellen einer reellwertigen Funktion. Der durch Widerspruch geführte Beweis zeigt auf, dass für unendlich oft sein Vorzeichen wechseln muss, was mit dem Zwischenwertsatz schon zeigt, dass unendlich viele Nullstellen auf besitzt.[143]
Es gibt heutzutage mehrere Beweise für den Satz von Hardy.[144] Einer hiervon macht Gebrauch von einem Satz von Leopold Fejér aus der Analysis. Dieser besagt, dass für eine positive reelle Zahl die Anzahl der Vorzeichenwechsel innerhalb einer auf stetigen (reellen) Funktion nicht kleiner ist als die Zahl der Vorzeichenwechsel in der Folge
Für den Beweis des Satzes von Hardy macht man dann von der Integralgleichung
Gebrauch.[145] Wegen wechselt die rechte Seite für unendlich oft ihr Vorzeichen. Nachweislich haben aber weder der Kosinus Hyperbolicus noch die Funktion positive Nullstellen, weshalb alle Vorzeichenwechsel von der Xi-Funktion, also letztlich der Zeta-Funktion, ausgehen müssen.
-
Schaubild der Funktion . Diese korrespondiert zur Grenzfunktion des ersten Integrals im Satz von Fejér. Zu erkennen sind die ersten „reellen Wurzeln“ der Gleichung und die damit korrespondierenden Vorzeichenwechsel. Zu jeder dieser Nullstellen wechselt die Funktion auch das Vorzeichen, da diese bisher sämtlich einfache Nullstellen sind.

Der Satz von Hardy liefert a priori keinen Beweis der Riemannschen Vermutung, da „unendlich viele“ nicht zwangsläufig „alle“ bedeutet. In etwa gibt es unendlich viele gerade Zahlen, aber nicht alle natürlichen Zahlen sind gerade.
Im Jahr 1921 verbesserte Hardy zusammen mit seinem Freund und Kollegen John Edensor Littlewood die Aussage auf das wesentlich stärkere Resultat, dass für hinreichend große Werte die Anzahl der Nullstellen auf der kritischen Geraden im Segment mindestens beträgt, wobei eine positive Konstante bezeichnet.
Atle Selberg verbesserte dieses Ergebnis 1942 auf [142] und zeigte damit, dass ein positiver Anteil aller Nullstellen auf der kritischen Geraden liegt.[146] Es gibt also eine Konstante , sodass
wobei die gesamte Anzahl von Nullstellen mit bezeichnet. Für diesen und andere Beiträge wurde er im Jahre 1950 mit der Fields-Medaille geehrt. Ab diesem Punkt wurde daran gearbeitet, möglichst hohe Werte für zu finden.
Anteile nichttrivialer Nullstellen auf der kritischen Geraden Bearbeiten
Im Jahr 1973 konnte Norman Levinson zeigen, dass mindestens ein Drittel () der nicht-trivialen Nullstellen auf der kritischen Geraden liegen muss, also , wobei jedoch als hinreichend groß vorausgesetzt wird.[147] Es war das erste explizite Resultat über die Proportion der nichttrivialen Nullstellen auf der kritischen Geraden, obwohl auch Selbergs ursprüngliche Methode hätte effektiv gemacht werden können.[148] 1975 konnte er die Schranke auf verbessern.[149] Das Resultat, sowie auch dessen Beweisidee, steht in einem engen Zusammenhang zum Nullstellenverhalten der ersten Ableitung der Zeta-Funktion im Streifen . Ein Nebenprodukt ist außerdem die Erkenntnis, dass höchstens 66 Prozent der Nullstellen auf der kritischen Geraden eine Ordnung höher als 1 haben können.[150] Im Kern verwendet die Methode die Funktionalgleichung der Zeta-Funktion und damit einhergehend, dass immer dann wenn
wobei und den Hauptzweig des komplexen Arguments bezeichnet.

Geringfügig verbesserte Werte stammen 1979 von Shi-Tuo Lou ()[151] und 1983 von Brian Conrey ().[152] Conrey hatte dabei nicht nur die Zeta-Funktion selbst, sondern auch die Ableitungen der Xi-Funktion studiert. Bezeichne die Anzahl der Nullstellen von mit . Dabei bezeichnet die -te Ableitung von . Conrey definierte zusätzlich die Größen
mit und . Durch eine komplizierte Version der Methode von Levinson bewies er
und allgemein für .[153] Durch eine Technik, die jener beim Beweis der Riemann-von-Magoldtschen Formel für ähnelt, kann zudem
gezeigt werden, wobei die Anzahl der Nullstellen von im Bereich und bezeichnet. Somit zeigt Conreys Resultat, dass in einem gewissen Sinne „fast alle“ Nullstellen der Funktion für auf der kritischen Geraden liegen.[154] Aleksandar Ivić schätzte es jedoch als „sehr unwahrscheinlich“ ein, dass sich Levinsons Methodik auch für einen Beweis der Aussage eignet, dass 100 Prozent der nichttrivialen Nullstellen auf der kritischen Geraden liegen.[155] Da 100 Prozent aber lediglich asymptotisch zu verstehen ist im Sinne von
wäre auch dies noch kein Beweis der Riemannschen Vermutung.
1989 verbesserte Conrey diesen Wert weiter auf , wobei er wiederum Techniken von Levinson verfeinerte.[156] In einem asymptotischen Sinne liegen also mehr als 40 % der nichttrivialen Nullstellen auf der kritischen Geraden. Im Jahr 2020 zeigten Kyle Pratt, Nicolas Nobles, Alexandru Zaharescu und Dirk Zeindler, dass mehr als aller Nullstellen auf der kritischen Geraden liegen.[157]
Nullstellenfreie Regionen Bearbeiten

Bereits Ende des 19. Jahrhunderts konnte mit Hilfe eines einfachen Widerspruchsbeweises gezeigt werden, dass die Zeta-Funktion keine Nullstellen auf der Geraden besitzt. Grundlage dieses Beweises ist die von Franz Mertens gezeigte, für alle mit gültige Ungleichung[158]
Ein wichtiger Zwischenschritt beim Beweis dieser Ungleichung ist die trigonometrische Identität sowie das Euler-Produkt.[159] Es gab seit dem Bemühungen, bessere nullstellenfreie Bereiche im kritischen Streifen zu finden. In diesen kann, teils durch mathematisch sehr aufwändige Schätzverfahren, das Auftreten einer Nullstelle ausgeschlossen werden. Jedoch ist diesen Bereichen gemein, dass ihre „Güte“ mit wachsendem Imaginärteil der Eingabe abnimmt. Also werden diese Bereiche zunehmend dünner und verlieren an Aussagekraft.
Die Existenz des bereits als „klassisch“ bezeichneten nullstellenfreien Bereichs
mit einer Konstanten war bereits Charles-Jean de La Vallée Poussin bekannt.[160]
Das bis heute schärfste nullstellenfreie Gebiet, mit großem technischem Aufwand gewonnen, ist für gegeben durch[161]
Es ist die Konsequenz einer von Nikolai Michailowitsch Korobow und Iwan Matwejewitsch Winogradow im Jahr 1958 bewiesenen oberen Schranke für die Zeta-Funktion.[162] Dieses Gebiet führt beim Primzahlsatz zur bis heute besten Fehlerabschätzung. Für eine Konstante gilt[163][164]
was von der durch die Riemannhypothese postulierten Fehlergröße jedoch noch weit entfernt ist. Ein expliziter Wert für die Konstante in der Fehlerfunktion, nämlich , wurde 2002 von Ford gegeben.[161] Insbesondere ist nicht bekannt, ob es ein gibt, sodass gilt für alle mit .[165]
Nichtkommutative Geometrie Bearbeiten
Ein vom Fields-Medaillen-Preisträger Alain Connes 1996 im Rahmen der von ihm entwickelten Nichtkommutativen Geometrie angegebener Operator passt „fast“. Connes konnte aber bisher nicht die Existenz weiterer Nullstellen außerhalb der kritischen Geraden ausschließen.[166]
Numerische Untersuchungen Bearbeiten
Bereits 1903 veröffentlichte Jørgen Pedersen Gram numerische Näherungswerte für die ersten 15 im kritischen Bereich liegenden Nullstellen.[167] Im Jahr 1936 hatte der in Oxford wirkende Mathematiker Edward Charles Titchmarsh mit einer Maschine, die ursprünglich für astronomische Berechnungen konstruiert worden war, die ersten 1.041 nicht-trivialen Nullstellen der Zeta-Funktion berechnet.[168] Im Jahr 1953 wurden diese Berechnungen von Alan Turing fortgesetzt. Seine Methode wird bis heute benutzt. Erstmals kam dabei ein Computer zum Einsatz.[169][170]
Ab Beginn der 1980er Jahre wurden die Computer immer leistungsstärker. Bereits im Jahr 1979 hatte eine Gruppe aus Amsterdam um Herman te Riele und Richard P. Brent 200 Millionen Nullstellen überprüft (etwas später erhöhten sie ihre Rechnung auf 300 Millionen) – alle lagen auf der kritischen Geraden. Damit widersprachen sie einer Vorhersage von Don Zagier, der geäußert hatte, es sei „ein Wunder“, falls diese immer noch ausnahmslos auf der kritischen Geraden lägen.[171] Zagier berief sich dabei auf theoretische Gründe, die zwar die Lage der ersten paar Tausend Nullstellen auf der Geraden bekräftigten, jedoch für steigende Zahlen schwächer – und letztlich sogar dagegen sprechend – auszulegen waren.

Bis 2005 wurden im Rahmen des sog. ZetaGrid Project, unter Benutzung der Methode des verteilten Rechnens, an der viele tausend Internetnutzer teilnahmen, die ersten 900 Milliarden Nullstellen überprüft. Um dieselbe Zeit berechnete Xavier Gourdon mit Unterstützung von Patrick Demichel bis Oktober 2004 die ersten 10 Billionen () Nullstellen, wobei sie das Verfahren von Odlyzko und Schönhage nutzten.[172][173] Alle lagen auf der kritischen Geraden.
Obwohl es sich bei allen Rechnungen um numerische Verfahren handelt, zeigen diese exakt und nicht nur annähernd, dass sich die untersuchten Nullstellen auf der kritischen Geraden befinden.[174] Das verwendete Verfahren nutzt einige Sätze aus der Funktionentheorie, wie den Residuensatz sowie das Prinzip vom Argument. Eine Berechnungsmöglichkeit sieht wie folgt aus: Bezeichnet die Anzahl der Nullstellen im Rechteck mit den Ecken und , so gilt
Dabei bezeichnet ein Umlaufintegral, wobei der Rand von in einfach mathematisch positiver Richtung durchlaufen wird, und ferner sei nicht der Imaginärteil einer Nullstelle der Zeta-Funktion. In diesem Integral kann die Zeta-Funktion und ihre Ableitung beliebig genau über die Euler-Maclaurin-Formel oder die Riemann-Siegel-Formel berechnet werden. Da die Größe eine ganze Zahl ist, kann das Endergebnis nach hinreichend guter Rechenarbeit durch Runden gefunden werden. Da jedoch stetig und reell für reelles ist, gibt es zwischen zwei beliebigen Punkten, an denen sich das Vorzeichen ändert, eine Nullstelle ungerader Ordnung. Durch geschickte Wahl von Zwischenstellen kann man Vorzeichenwechsel von im Intervall ermitteln. Wenn die Anzahl der Vorzeichenwechsel gleich ist, kann man daraus schließen, dass alle Nullstellen von in einfach sind und die Riemannsche Vermutung erfüllen.[175]
Weitere äquivalente Aussagen Bearbeiten
Die Suche nach zur Riemannhypothese äquivalenten Aussagen war und ist Gegenstand intensiver Forschung. Kann eine dieser Aussagen beweisen werden, folgt die Riemannsche Vermutung. Andersherum hat ein Beweis der Riemannschen Vermutung auch die Gültigkeit der äquivalenten Aussage zur Konsequenz. Keine der eingeschlagenen Richtungen hat bisher jedoch zu neuen Erkenntnissen über die Zeta-Funktion geführt, und es ist nicht bekannt, ob sie als wirklichen Fortschritt zur Lösung des Problems gewertet werden können.[176]
Arithmetik Bearbeiten
Teilersummen Bearbeiten

Die Riemannsche Vermutung zieht nicht nur Konsequenzen für die Verteilung der Primzahlen, sondern auch das Verhalten von Teilern ganzer Zahlen nach sich. Dies betrifft zum Beispiel die Teilerfunktion
- ,
also die Summe aller positiven Teiler einer Zahl – so ist etwa . Zum Beispiel besagt das Ramanujan-Robin-Kriterium (nach Srinivasa Ramanujan und Guy Robin), dass die Riemannhypothese genau dann zutrifft, wenn die Ungleichung
für alle erfüllt ist.[177] Dabei ist die Euler-Mascheroni-Konstante, die Eulersche Zahl und der natürliche Logarithmus. Robin selbst bewies die schwächere Abschätzung[178]
Ähnlich dazu ist das von Jeffrey Lagarias gefundene Kriterium, das besagt, dass die Riemannsche Vermutung äquivalent ist zur Ungleichung
- ,
wobei und die -te harmonische Zahl bezeichnet.[179]
Eulersche Phi-Funktion Bearbeiten
Die Eulersche Phi-Funktion an der Stelle zählt die Anzahl der zu teilerfremden Zahlen, die höchstens sind. Etwa ist , denn es gibt nur zwei Zahlen , die teilerfremd zu sind: und . Da es natürlich nur natürliche Zahlen bis gibt, gilt nach Definition , doch das genaue Verhalten von beugt sich, ähnlich wie im Falle der Primzahlen, keinem einfachen Prinzip. In etwa ist der Quotient für wachsende nicht konvergent und unterliegt starken Schwankungen. Die Riemannsche Vermutung ist äquivalent zu der Aussage (erstes Kriterium von Jean-Louis Nicolas), dass[180]
für alle gilt, wobei die -te Primzahl, das Primorial von , die Euler-Mascheroni-Konstante und die Eulersche Zahl bezeichnet. Ist sie hingegen falsch, so ist diese Ungleichung für eine unendliche Zahl an Werten wahr und für eine unendliche Zahl an Werten falsch. Zudem trifft sie genau dann zu, falls[180]
Dabei bezeichnet den Limes superior. Das Ergebnis stammt ebenfalls von Nicolas.
Analysis Bearbeiten
Asymptotische Analysis Bearbeiten
Schon 1916 hatte der Mathematiker Marcel Riesz gezeigt, dass die Riemannsche Vermutung äquivalent ist zu der Aussage
für alle .[181] Nachweislich handelt es sich bei der Potenzreihe zur linken um eine ganze Funktion in .[182] Die Koeffizienten der Reihe alternieren, und so ist es schwierig, das exakte Wachstumsverhalten für größer werdende Werte von zu schätzen. Dieses Resultat bettet sich in eine ganze Reihe von Kriterien ein, die ganze Funktionen betreffen. Ist eine ganze Funktion mit
- ,
so sei die korrespondierende Funktion definiert durch
Da , haben die Potenzreihen zu und denselben Konvergenzradius. Es gelte für
- ,
und zusätzlich für
- .
Das Báez-Duarte-Kriterium besagt, dass die Riemannsche Vermutung dann äquivalent ist zu für .[183]
Funktionalanalysis Bearbeiten
Ein aus mathematischer Sicht überraschender Zusammenhang zur Riemannhypothese besteht zu Dichtheitsaussagen von Teilräumen von Banach- und Hilbert-Räumen. Dazu zählt das Kriterium von Nyman, benannt nach Bertil Nyman. Für jedes definiere
- ,
wobei die Gauß-Klammern bezeichnet. Die Riemannsche Vermutung ist dann äquivalent dazu, dass das lineare Erzeugnis der Menge dicht in (siehe auch Lp-Raum) liegt.[184] Arne Beurling verallgemeinerte die Arbeit von Nyman. Dazu definiert man den reellen Vektorraum
- ,
wobei den fraktionalen Teil von bezeichnet. Das Nyman-Beurling-Kriterium besagt, dass für der Raum genau dann dicht im Banach-Raum liegt, wenn die Riemannsche Zeta-Funktion keine Nullstellen in der Halbebene besitzt.[185]
Varianten und Verallgemeinerungen Bearbeiten
Verallgemeinerte Riemannsche Vermutung Bearbeiten
Die verallgemeinerte Riemannsche Vermutung (englisch Generalized Riemann Hypothesis (GRH)) dehnt die Aussage der Riemannhypothese auf den Fall von L-Funktionen zu Dirichlet-Charakteren aus, also auf die sog. Dirichletschen L-Funktionen. Dabei wird zunächst einem Dirichlet-Charakter (einer periodischen, streng multiplikativen zahlentheoretischen Funktion) eine Dirichlet-Reihe mit Euler-Produkt zugeordnet via
Erneut ist diese Darstellung nur für Werte gültig, und die Funktionen lassen sich analytisch auf ganz fortsetzen, wobei in ein Pol erster Ordnung im Falle eines Hauptcharakters, d. h., nimmt an allen Stellen ungleich Null bloß den Wert 1 an, und ansonsten eine hebbare Singularität vorliegt. In letzterem Fall dehnt sich sogar zu einer ganzen Funktion aus. Die verallgemeinerte Riemannsche Vermutung besagt nun, dass alle (nichttrivialen) Nullstellen von im Streifen den Realteil haben.[186] Aus der verallgemeinerten Riemannschen Vermutung folgt die Riemannsche Vermutung mit als Spezialfall.
Kurz gesagt überträgt die verallgemeinerte Riemannsche Vermutung Folgerungen der Riemannhypothese auch auf Primzahlen in arithmetischen Progressionen, also etwa den Primzahlen in der Progression 7, 1007, 2007, 3007, … Sie stellt damit etwa eine starke Verschärfung des Dirichletschen Primzahlsatzes bzw. Satzes von Siegel-Walfisz dar, indem sie auch hier eine Fehlergröße der Hauptabschätzung in den Bereich einer Quadratwurzel verordnet.[187] Andrew Granville konnte zeigen, dass die (starke) Goldbachsche Vermutung im Wesentlichen zur verallgemeinerten Riemannschen Vermutung äquivalent ist.[188] Eine andere Anwendung betrifft den sog. Tschebyschow Bias, eine Aussage, dass es in einem gewissen Sinne mehr Primzahlen gibt also solche mit . Unter Annahme der GRH für den nichttrivialen Dirichlet-Charakter modulo 4 konnte
im Jahr 1914 von Godfrey Harold Hardy und John Edensor Littlewood gezeigt werden.[189]
Zahlkörper Bearbeiten
Die Dedekindsche Zeta-Funktion eines Zahlkörpers verallgemeinert die Riemannsche Zeta-Funktion. Dabei befasst sich mit der „Primfaktorzerlegung“ im Ganzheitsring von . Der Ring ist die Menge aller Elemente , die Lösung einer Polynomgleichung mit ganzen Zahlen sind.[190] Zum Beispiel ist und . Die Frage, ob es allgemein in eine eindeutige Zerlegung in Primelemente gibt, ist von zahlentheoretischer Relevanz und ihre Antwort lautet im Allgemeinen „Nein“. So sind die Zahlen zwar alle prim und paarweise verschieden in , jedoch gilt
Um Eindeutigkeit wieder herzustellen, wird auf die Ideale von übergegangen. Vor diesem Hintergrund entwickelte Ernst Eduard Kummer die Idee der „idealen Zahlen“, die jedoch als überholt gilt.[191] Es kann gezeigt werden, dass jedes nicht-triviale ganze Ideal eine eindeutige multiplikative Zerlegung in Primideale besitzt. Dies ermöglicht schließlich die Definition einer Zeta-Funktion
die in ein Euler-Produkt über die Primideale zerfällt:[192]
Hierbei bezeichnet die natürliche Zahl die Norm des Ideals (ein Maß für seine „Dichte“ in ).
Die Funktion besitzt eine holomorphe Fortsetzung nach , hat einen Pol erster Ordnung in und erfüllt eine Funktionalgleichung.[193] Die Riemannsche Vermutung für Zahlkörper besagt nun, dass alle nichttrivialen Nullstellen der Funktion den Realteil besitzen.
Eine Folgerung der Riemannhypothese für Zahlkörper ist die Richtigkeit der Artinschen Vermutung.
Grand Riemann Hypothesis Bearbeiten
Im Rahmen der Grand Riemann Hypothesis (deutsch: „Große Riemannsche Vermutung“) wird die Riemannhypothese auf eine sehr weite Klasse sog. L-Funktionen ausgeweitet. Das betrifft L-Funktionen, die automorphen Darstellungen zugeordnet sind. Der einfachste Fall sind hier Darstellungen der Dimension 1, also Dirichletsche L-Funktionen, weshalb die Grand Riemann Hypothesis die verallgemeinerte Riemannsche Vermutung beinhaltet. Der Fall der Dimension 2 betrifft L-Funktionen bezüglich Modulformen, wobei der Fall zu Spitzenformen besonders interessant ist. Ein Beispiel ist
wobei
und die Diskriminante, eine Spitzenform mit Gewicht 12, und die Ramanujansche tau-Funktion bezeichnet. Ganz allgemein kann die L-Funktion zu einer Darstellung nur mit Begriffen der höheren Mathematik erfasst werden. Man beginnt mit dem Adelering der rationalen Zahlen und betrachtet eine automorphe, cuspidale Darstellung von (wobei GL die allgemeine lineare Gruppe bezeichnet). Diese ist nun äquivalent zu mit () oder , wobei eine irreduzible unitäre Darstellung der und eine Primzahl ist. Zu jeder Primzahl kann nun ein lokaler Faktor
mit komplexen Parametern , die von bestimmt sind, gebildet werden. Auf ähnliche Weise erhält man für einen Gamma-Faktor
wobei Aus den lokalen Euler-Faktoren kann damit ein globales Objekt konstruiert werden via
Mit der Automorphie von kann gezeigt werden, dass sich die Komplettierung zu einer ganzen Funktion fortsetzt und eine Funktionalgleichung unter erfüllt. Die Grand Riemann Hypothesis besagt, dass alle Nullstellen von im Bereich den Realteil haben.[194]
Es wird im Rahmen des Langlands-Programms vermutet, dass sich „alle“ L-Funktionen, insbesondere die für die Arithmetik interessanten Dirichletschen-, Dedekindschen-, Heckeschen-, Artinschen-, Hasse-Weil- Zeta- bzw. L-Funktionen aus den oben genannten multiplikativ Zusammensetzen, womit die Riemannsche Vermutung in diesen Fällen aus der Grand Riemann Hypothesis folgen würde.[195]
Varietäten über endlichen Körpern Bearbeiten
Während der Fall globaler Körper allgemein offen ist, wurden im 20. Jahrhundert bedeutende Fortschritte in der Theorie lokaler Körper, der Funktionenkörper und endlicher Körper erreicht. Ähnlich wie die Dedekindsche Zeta-Funktion arithmetische Daten eines (globalen) Zahlkörpers in sich kodiert, können Varietäten, also Lösungen von Polynomgleichungen, über endlichen Körpern Zeta-Funktionen zugeordnet werden. Am einfachsten sind hier Kurven, die aus den Lösungen einer einzigen Gleichung in zwei Variablen aufgebaut sind, etwa . Dabei werden also die Lösungen innerhalb der Koordinatenraums betrachtet, wobei ein endlicher Körper ist. Die zugehörige Zeta-Funktion einer Kurve über mit , mit einer Primzahlpotenz , kann wie folgt definiert werden:
wobei die natürliche Exponentialfunktion, die Körpererweiterung von vom Grade ist und die Anzahl von Lösungen der Gleichung in .[196] Die Riemannsche Vermutung besagt dann, dass diese Zeta-Funktion stets eine Funktionalgleichung erfüllt und alle Nullstellen den Realteil besitzen. Der Fall von Kurven des Geschlechts , sog. elliptischer Kurven, wurde dabei im Jahr 1934 von Helmut Hasse, und für beliebiges Geschlecht von André Weil in den 1940ern bewiesen.[197] Weil vermutete überdies, dass sich die Riemannhypothese auch auf den Fall sämtlicher Varietäten über endlichen Körpern ausdehnen sollte, also Nullstellengebilde von beliebigen Systemen von Polynomgleichungen (beliebig, aber endlich viele Polynome in beliebig vielen Variablen). Diese sog. Weil-Vermutungen konnten erst 1974 durch Pierre Deligne bewiesen werden, nach bedeutender Vorarbeit von Alexander Grothendieck, Emil Artin und Jean-Louis Verdier, welche die étale Kohomologie entwickelten. Diese ist ein zentrales Werkzeug in Delignes Beweis, der außerordentlich hoch in seiner Schwierigkeit ist und zu den bedeutendsten Fortschritten der Mathematik des 20. Jahrhunderts zählt.[198]
Rezeption Bearbeiten
In Fachkreisen Bearbeiten
Nach Meinung vieler führender Mathematiker ist die Riemannsche Vermutung, zusammen mit ihren Verallgemeinerungen auf L-Funktionen, das derzeit wichtigste offene Problem der reinen Mathematik.[49]
Der deutsche Fields-Medaillen-Träger Gerd Faltings nennt das Problem „wirklich wichtig“ und schätzt es als jenes mit derzeit „höchstem Prestige“ ein. Bezüglich der Rolle Riemanns weist er darauf hin, dass dieser es „ja nicht wirklich vermutet“ habe, sondern lediglich „gefragt habe, ob es so sei“.[199]
Peter Borwein, Stephen Choi, Brendan Rooney und Andrea Weirathmueller bezeichnen die Riemannsche Vermutung als „Heiligen Gral“ unter den mathematischen Problemen. Die Lösung eines solchen Problems sei stets wie die Erstbesteigung des Mount Everest, jedoch seien viele „große Probleme“ eher „isolierte Gipfel“ gewesen, wie etwa das Fermat-Problem als solches. Bei der Riemannhypothese sei dies aber „anders“, da eine Menge ungelöster Probleme aus ihr folgen würden.[200]
Atle Selberg hielt die Riemannhypothese für wahr und gab 1946 folgende Einschätzung:
„Ich denke, wir glauben deshalb so gerne an die Richtigkeit der Riemannschen Vermutung, weil es die schönste und einfachste Verteilung für die Nullstellen ist, die wir uns vorstellen können. Es gibt diese Symmetrie entlang der kritischen Geraden. Außerdem hätte sie die natürlichste Verteilung der Primzahlen zur Folge. Irgendwie möchten wir gerne glauben, dass zumindest etwas in diesem Universum richtig sein sollte.“
Film und Fernsehen Bearbeiten
In der Folge Prime Suspect (Staffel 1, Folge 5) der Serie Numbers – Die Logik des Verbrechens wird die Tochter Emily (Emma Prescott) des Mathematikers Ethan Burdick (Neil Patrick Harris) entführt, der von sich behauptet, die Riemannsche Vermutung bewiesen zu haben. Ethan Burdick fürchtet indes „Diebstahl und eine Sabotage“ seiner Arbeit durch einen Rivalen.[202]
In der Literatur Bearbeiten
Harold Davenport berichtete, dass sich Godfrey Harold Hardy und John Edensor Littlewood beinahe zerstritten, da Hardy eine Kriminalgeschichte verfasst hatte, in der ein Mathematiker die Riemannsche Vermutung bewiesen hatte, dann aber von einem zweiten Mathematiker ermordet wurde, da dieser den Beweis für sich beanspruchen wollte. Littlewood war nicht primär wegen der hintergründigen Tatsache verärgert, dass er äußerst viel mit Hardy publizierte, aber ein Mitautor des fiktiven Beweises unerwähnt blieb, sondern der Mörder eine gewisse Ähnlichkeit mit ihm habe. Er bestand darauf, dass Hardy das Manuskript nie veröffentlichen sollte, und dieser gab schließlich nach.[203]
Im Roman Die Riemannsche Vermutung (2006, Roten av minus én, dt. Wurzel aus Minus eins) des norwegischen Schriftstellers Atle Næss wird teilweise Bezug auf das mathematische Problem genommen.[204]
In dem Roman Life After Genius von M. Ann Jacoby (2008) versucht die Hauptfigur Theodore „Mead“ Fegley, der erst 18 Jahre alt ist und sich im letzten Semester des Colleges befindet, die Riemannhypothese für sein Forschungsprojekt im letzten Studienjahr zu beweisen. Er benutzt auch einen Supercomputer, um mehrere Milliarden Nullstellen der Riemannschen Zeta-Funktion zu berechnen. In mehreren Traumsequenzen innerhalb des Buches führt Mead einige Gespräche mit Bernhard Riemann über das Problem und die Mathematik im Allgemeinen.[205]
In dem 2013 veröffentlichten Roman The Humans von Matt Haig (dt. Ich und die Menschen, 2014) ermorden überlegene Außerirdische einen genialen Mathematikprofessor, der die Riemannsche Vermutung bewiesen hatte, und entsenden einen der Ihren in seinen freigewordenen Körper, um die Spuren dieser Entdeckung auszutilgen, einschließlich aller Personen, die davon wissen könnten. Sie sind der Meinung, dass die Menschheit noch lange nicht reif sei für die weitreichenden Folgen dieser Entdeckung und das Universum vor den Menschen geschützt werden müsse.
Literatur Bearbeiten
- Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. dtv / C.H.Beck, München 2003 und 2004, ISBN 3-423-34299-4 (populäre Darstellung der Geschichte der Vermutung).
- Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis. Cambridge University Press, 2015, ISBN 978-1-107-49943-0, (Entwurf 2013 als PDF; 7,6 MB). ( vom 15. September 2013 im Internet Archive).
- John Derbyshire: Prime obsession – Bernhard Riemann and the greatest unsolved problem in Mathematics. Washington 2003, ISBN 0-309-08549-7.
- Harold Edwards: Riemann’s Zeta Function. New York 1974, Dover 1991, ISBN 0-486-41740-9.
- Karl Sabbagh: Dr. Riemann’s zeros. Atlantic books, London 2002.
- Edward Charles Titchmarsh: The Theory of the Riemann Zeta-Function. Bearbeitet von Heath-Brown. Clarendon, Oxford 1987, ISBN 0-19-853369-1.
- P. Borwein, S. Choi, B. Rooney, A. Weirathmueller: The Riemann hypothesis. A resource for the afficionado and virtuoso alike. (CMS Books in Mathematics 27) Canad. Math. Soc., Springer-Verlag, o. O. 2008, ISBN 978-0-387-72125-5.
- Julian Havil: Gamma – Eulers Konstante, Primzahlstrände und die Riemannsche Vermutung. Springer Verlag, o. O. 2007.
- Jürg Kramer: Die Riemannsche Vermutung. In: Elemente der Mathematik. Band 57, 2002, S. 90–95. hu-berlin.de. (PDF; 400 kB).
- Dan Rockmore: Stalking the Riemann Hypothesis. Pantheon Books, New York 2005.
- Kevin Broughan: Equivalents of the Riemann Hypothesis. 2 Bände, Cambridge University Press, Cambridge 2017.
Weblinks Bearbeiten
Texte Bearbeiten
- Christopher Deninger: Primzahlen und die Riemannsche Vermutung. ( vom 1. Juni 2010 im Internet Archive). (PDF; 350 kB).
- Alain Connes: An Essay on the Riemann hypothesis, 2015, Arxiv.
- Xavier Gourdon: The 10^13 first zeros of the Riemann Zeta function, and zeros computation at very large height. (PDF; 413 kB).
- Clay Mathematics Institute zur Riemannschen Vermutung mit Faksimile von Riemanns Arbeit und Bombieris sowie Sarnaks offizieller Beschreibung.
Videos Bearbeiten
- 3Blue1Brown: Visualizing the Riemann zeta function and analytic continuation auf YouTube, 9. Dezember 2016.
- Weitz / HAW Hamburg: Die Riemannsche Vermutung (Weihnachtsvorlesung 2016) auf YouTube, 12. Mai 2017.
- Mathewelten / ARTE: Die Riemannsche Vermutung auf YouTube, 11. Dezember 2021.
Anmerkungen Bearbeiten
- ↑ Zum Beispiel über die erzeugende Funktion.
- ↑ Für wird aus der Näherung eine Gleichheit.
- ↑ Es ist jedoch zu beachten, dass die Existenz einer Funktionalgleichung dieses Typs kein hinreichendes Werkzeug für einen Beweis der Riemannschen Vermutung darstellen kann. Es muss über ein Euler-Produkt zusätzlich eine „arithmetische Komponente“ mitwirken. So gibt es Dirichlet-Reihen, deren Komplettierungen mit einem Gamma-Faktor zwar eine analoge Funktionalgleichung, jedoch kein Euler-Produkt besitzen, und für welche die Riemannsche Vermutung erwiesenermaßen falsch ist.
Einzelnachweise Bearbeiten
- ↑ Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. viii.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 5.
- ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers, American Mathematical Society, Vol. 203, 2020, S. 57.
- ↑ Alain Connes: An Essay on the Riemann Hypothesis In: John Forbes Nash u. Michael Th. Rassias (Hrsg.): Open Problems in Mathematics. Springer, S. 228.
- ↑ Simon Rubinstein-Salzedo: Cryptography, Springer, S. 137.
- ↑ Don Zagier: Die ersten 50 Millionen Primzahlen, Elemente der Mathematik, Band 15, Birkhäuser, S. 4.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 2.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 1.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 2.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory, Springer Monographs in Mathematics, S. 13.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 4.
- ↑ Carl Friedrich Gauss Werke, Zweiter Band, Herausgegeben von der königlichen Gesellschaft der Wissenschaften zu Göttingen, 1863, (Brief), S. 444–447.
- ↑ a b Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 41.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory, Springer Monographs in Mathematics, S. 183.
- ↑ Tom M. Apostol: Introduction to Analytic Number Theory. Springer, 1976, S. 74.
- ↑ Joel Spencer, Ronald Graham: The Elementary Proof of the Prime Number Theorem. Mathematical Intelligencer 2009, Nr. 3.
- ↑ Florian K. Richter: A new elementary proof of the Prime Number Theorem, Bulletin of the London Mathematical Society, Volume 53, Issue 5, S. 1365–1375.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, S. 216–217.
- ↑ a b Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. 41.
- ↑ David J. Platt: Computing analytically, Mathematics of Computation, Vol. 84, Nr. 293, May 2015, S. 1532 (Theorem 7.1).
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume One: Arithmetic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 164, S. 22.
- ↑ Schoenfeld, Lowell (1976): Sharper bounds for the Chebyshev functions and . II. Mathematics of Computation, 30 (134): S. 337–360, Corollary 1, (PDF).
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer, 1992, S. 453.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 93.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 87–90.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 188.
- ↑ Steven J. Miller, Ramin Takloo-Birhash: An Invitation to Modern Number Theory, Princeton University Press, S. 274.
- ↑ A. Klenke: Wahrscheinlichkeitstheorie, 3. Auflage, Springer, siehe Kapitel 15.
- ↑ Arpita Kar, M. Ram Murty: The Central Limit Theorem in Algebra and Number Theory, In: B. Ramakrishnan, Bernhard Heim, Brundaban Sahu (edt.): Modular Forms and Related Topics in Number Theory, S. 101.
- ↑ a b c d P. Borwein, S. Choi, B. Rooney, A. Weirathmueller: The Riemann hypothesis. A resource for the afficionado and virtuoso alike. (CMS Books in Mathematics 27) Canad. Math. Soc., Springer, 2008, S. 6.
- ↑ Terence Tao: Pseudorandomness properties of the Liouville function, Tao Lecture Series, Universität Bonn, abgerufen am 30. Dezember 2021.
- ↑ P. Borwein, S. Choi, B. Rooney, A. Weirathmueller: The Riemann hypothesis. A resource for the afficionado and virtuoso alike. (CMS Books in Mathematics 27) Canad. Math. Soc., Springer, 2008, S. 6–7.
- ↑ P. Borwein, S. Choi, B. Rooney, A. Weirathmueller: The Riemann hypothesis. A resource for the afficionado and virtuoso alike. (CMS Books in Mathematics 27) Canad. Math. Soc., Springer, 2008, S. 46.
- ↑ Enrico Bombieri: The Riemann hypothesis. In: J. Carlson, A. Jaffe, und A. Wiles (Hrsg.) The Millennium Prize Problems, Clay Mathematical Institute jointly with the American Mathematical Society, S. 111.
- ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers, American Mathematical Society, Vol. 203, 2020, S. 3–4.
- ↑ Terence Tao: Poincarés legacies: pages from year two of a mathematical blog, S. 621–622.
- ↑ Konrad Knopp: Theorie und Anwendung der unendlichen Reihen, 5. Auflage, Springer, S. 323.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory, Springer Monographs in Mathematics, S. 239, 253.
- ↑ D. Zagier: Newman’s short proof of the prime number theorem. In: The American Mathematical Monthly, Bd. 104, Nr. 8 (Oktober 1997), S. 705–708 (PDF).
- ↑ Enrico Bombieri: The Riemann hypothesis. In: J. Carlson, A. Jaffe, und A. Wiles (Hrsg.) The Millennium Prize Problems, Clay Mathematical Institute jointly with the American Mathematical Society, S. 107.
- ↑ Hugh L. Montgomery, Robert C. Vaughan: Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics, S. 185.
- ↑ Hugh L. Montgomery, Robert C. Vaughan: Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics, S. 328.
- ↑ Tom M. Apostol: Introduction to Analytic Number Theory. Springer, 1976, S. 229–231.
- ↑ a b Hugh L. Montgomery, Robert C. Vaughan: Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics, S. 22.
- ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers, American Mathematical Society, Vol. 203, 2020, S. 64.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 43.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 51.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 37.
- ↑ a b Enrico Bombieri: The Riemann hypothesis. In: J. Carlson, A. Jaffe, und A. Wiles (Hrsg.) The Millennium Prize Problems, Clay Mathematical Institute jointly with the American Mathematical Society, S. 108.
- ↑ J. B. Conrey, A. Ghosh und S. M. Gonek: Simple Zeros of the Riemann Zeta‐Function, Proceedings of the London Mathematical Society, Volume 76, Issue 3, S. 497.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 176.
- ↑ Peter Scholze, Jakob Stix: Why abc is stil a conjecture, abgerufen am 4. Januar 2022.
- ↑ Inter-universal Teichmüller Theory IV: Log-volume computations and set-theeoretic foundations, Research Institute for Mathematical Sciences, Kyoto University, abgerufen am 4. Januar 2022.
- ↑ Helge von Koch: Sur la distribution des nombres premiers. Acta Mathematica, Band 24, 1901, S. 159–182.
- ↑ Gerald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Third Edition, S. 271.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 130.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 131–133.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 133.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 136.
- ↑ Gerald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Third Edition, S. 277–291.
- ↑ Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. 87.
- ↑ Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. 88.
- ↑ Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. 87–88.
- ↑ Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. 90–93.
- ↑ Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. 103.
- ↑ Terence Tao: E pluribus unum: From Complexity, Universality, Dædalus, the Journal of the American Academy of Arts & Sciences, S. 30–31.
- ↑ Barry Mazur, William Stein: Prime Numbers and the Riemann Hypothesis, Cambridge University Press, S. 136–138.
- ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers, American Mathematical Society, Vol. 203, 2020, S. 57.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 217.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 217–218.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 218.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 226.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 232.
- ↑ Terence Tao: An Epsilon of Room, II: pages from year three of a mathematical blog, American Mathematical Society, S. 213.
- ↑ D. A. Goldston, Y. Motohashi, J. Pintz, C. Y. Yıldırım: Small Gaps between Primes Exist. In: Japan Academy. Proceedings. Series A. Mathematical Sciences. 82(4), S. 61–65.
- ↑ D. A. Goldston, J. Pintz, C. Y. Yıldırım: Small gaps between primes II (Preliminary). Preprint, 8. Februar 2005.
- ↑ Yitang Zhang: Bounded gaps between primes. In: Annals of Mathematics. 179(3), 2014, S. 1121–1174.
- ↑ James Maynard: Small gaps between primes. In: Annals of Mathematics. Second Series, 181, 2015, S. 383–413.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 320.
- ↑ Neal Koblitz: A Course in Number Theory and Cryptography, Second Edition, Springer, 1994, Kapitel IV.
- ↑ Gary L. Miller: Riemann’s Hypothesis and Tests for Primality, Journal of Computer and System Sciences, 1976, 13(3): S. 300–317.
- ↑ M. O. Rabin: Probabilistic algorithm for testing primality, Journal of Number Theory, 1980, 12(1): S. 128–138.
- ↑ Eric Bach: Explicit bounds for primality testing and related problems, Mathematics of Computation, 1990, 55(191): S. 355–380.
- ↑ a b Aleksandar Ivić: The Riemann Zeta-Function. Theory and Applications. Dover Publications Inc., S. 48.
- ↑ Steven J. Miller, Ramin Takloo-Birhash: An Invitation to Modern Number Theory, Princeton University Press, S. 359.
- ↑ Steven J. Miller, Ramin Takloo-Birhash: An Invitation to Modern Number Theory, Princeton University Press, S. 360.
- ↑ Steven J. Miller, Ramin Takloo-Birhash: An Invitation to Modern Number Theory, Princeton University Press, S. 360–361.
- ↑ Steven J. Miller, Ramin Takloo-Birhash: An Invitation to Modern Number Theory, Princeton University Press, S. 384.
- ↑ Mark Kac: Comments on G. Pólya’s „Bemerkung uber die integraldarstellung der Riemannschen zeta-funktion“. (Acta Mathematica, Band 48, 1926, S. 305–317), in: Polya, Collected Works, Band 2, MIT Press 1974.
- ↑ Tsung-Dao Lee, Yang Chen-Ning: Statistical Theory of Equations of State and Phase Transitions. II. Lattice Gas and Ising Model, Physical Review, 87 (3): S. 410–419.
- ↑ Andreas Knauf: Number theory, dynamical systems and statistical mechanics, Reviews in Mathematical Physics, 11 (8): S. 1027–1060.
- ↑ Freeman Dyson: Birds and Frogs. In: Notices AMS. 2009. (PDF; 800 kB).
- ↑ Freeman Dyson: Quasi-Crystals and the Riemann Hypothesis. In: Hugh Montgomery, Ashkan Nikeghbali, Michael Th. Rassias (Hrsg.): Exploring the Riemann Zeta Function, Springer, S. v–vii.
- ↑ Bernhard Riemann: Über die Anzahl der Primzahlen unter einer gegebenen Größe. 19. Oktober 1859. In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin. 1860, S. 671–680.
- ↑ Siegel: Über Riemanns Nachlaß zur analytischen Zahlentheorie. In: Studien zur Geschichte der Math. Astron. und Phys. Abt. B: Studien, Band 2, 1932, S. 45–80.
Siegel: Gesammelte Abhandlungen. Band 1, Springer Verlag, 1966. - ↑ Laugwitz: Bernhard Riemann. 1996, S. 178.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 164–166.
- ↑ Andrew Odlyzko: On the Distribution of Spacings Between Zeros of the Zeta Function. In: Mathematics of Computations. Band 48, Nr. 117, 1987, S. 276.
- ↑ Peter Borwein et al.: The Riemann Hypothesis. Springer, New York 2008, Abschnitt 3.3, S. 32.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 164.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, S. 244–245.
- ↑ John Derbyshire: Prime Obsession. Joseph Henry Press, S. 354–355.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, S. 147.
- ↑ Julian Havil: Gamma. Springer-Verlag, Berlin et al. 2007, S. 245.
- ↑ 143 year old problem still has mathematicians guessing. In: New York Times. Die Anekdote ist auch in der Hilbert-Biografie von Constance Reid zu finden.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, S. 161.
- ↑ John Derbyshire: Prime Obsession. Joseph Henry Press, S. 353.
- ↑ a b John Derbyshire: Prime Obsession. Joseph Henry Press, S. 354.
- ↑ The Clay Mathematics Institute: Overview and History. In: Website des Clay Mathematics Institute, abgerufen am 22. Januar 2022.
- ↑ Rules for the Millennium Prizes. In: Website des Clay Mathematics Institute, abgerufen am 20. Februar 2022.
- ↑ Regeln des Millennium-Preises von der offiziellen Webseite, siehe Abschnitt 5. c. i.–ii.
- ↑ a b Emily Conover: Here’s why we care about attempts to prove the Riemann hypothesis. In: Science News, abgerufen am 12. Februar 2022.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory, Springer Monographs in Mathematics, S. 158–159.
- ↑ a b c Władysław Narkiewicz: The Development in Prime Number Theory, Springer Monographs in Mathematics, S. 159.
- ↑ Thomas Jean Stieltjes: Sur une fonction uniforme, Comptes Rendus Acad. Sci. Paris, Vol. 101, S. 153–154.
- ↑ Jacques Hadamard: Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques. In: Bulletin de la Société Mathématique de France. 24, 1896, S. 199–220. (PDF; 1,3 MB), dort S. 199 ff.
- ↑ Władysław Narkiewicz: The Development in Prime Number Theory, Springer Monographs in Mathematics, S. 160.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 263.
- ↑ Andrew Odlyzko, Herman te Riele: Disproof of the Mertens Conjecture, Journal für die reine und angewandte Mathematik, 1985 (357): S. 138–160.
- ↑ Andrew Hodges: Alan Turing: The Enigma, Vintage, Princeton University Press, 2014, S. 178.
- ↑ Edward Charles Titchmarsh: The Zeros of the Riemann Zeta-Function, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, The Royal Society, 1936, 151 (873): 234–255
- ↑ Andrew Hodges: Alan Turing: The Enigma, Vintage, Princeton University Press, 2014, S. 178–179.
- ↑ Andrew Hodges: Alan Turing: The Enigma, Vintage, Princeton University Press, 2014, S. 179.
- ↑ Andrew Hodges: Alan Turing: The Enigma, Vintage, Princeton University Press, 2014, S. 197–198.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, S. 238–239.
- ↑ Science: As You Were. In: Time Magazine (Monday, Apr. 30, 1945), abgerufen am 23. Januar 2022.
- ↑ Karl Sabbagh: Dr. Riemann’s Zeros, Atlantic Books London, S. 91.
- ↑ Karl Sabbagh: Dr. Riemann’s Zeros, Atlantic Books London, S. 87–88.
- ↑ It figures, Los Angeles Times, 15. Januar 1985.
- ↑ Karl Sabbagh: Dr. Riemann’s Zeros, Atlantic Books London, S. 95. Der dort angegebene Vorname Makoto von Matsumoto ist falsch.
- ↑ Karl Sabbagh: Dr. Riemann’s Zeros, Atlantic Books London, S. 96.
- ↑ Karl Sabbagh: Dr. Riemann’s Zeros, Atlantic Books London, S. 139–140.
- ↑ Karl Sabbagh: Dr. Riemann’s Zeros, Atlantic Books London, S. 140.
- ↑ Karl Sabbagh: Dr. Riemann’s Zeros, Atlantic Books London, S. 140–141.
- ↑ Kevin O’Sullivan: World of maths aflutter over new proof of 160-year-old hypothesis. In: Irish Times, abgerufen am 12. Februar 2022.
- ↑ Rhys Blakely: Sir Michael Atiyah: Age is just a number, says 89-year-old maths genius. In: The Times, abgerufen am 12. Februar 2022.
- ↑ Lecture: The Riemann Hypothesis, Heidelberg Laureate Forum, abgerufen am 12. Februar 2022.
- ↑ a b c Frankie Schembri: Skepticism surrounds renowned mathematician's attempted proof of 160-year-old hypothesis. In: Science, abgerufen am 12. Februar 2022.
- ↑ a b Gilead Amit: Riemann hypothesis likely remains unsolved despite claimed proof. In: New Scientist, abgerufen am 12. Februar 2022.
- ↑ a b On Michael Atiyah and the Riemann Hypothesis. In: American Mathematical Society Blogs, abgerufen am 12. Februar 2022.
- ↑ Godfrey H. Hardy: Sur les Zéros de la Fonction de Riemann, C. R. Acad. Sci. Paris, 158, S. 1012–1014 (1914).
- ↑ a b Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 226.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 226–229.
- ↑ Steven J. Miller, Ramin Takloo-Birhash: An Invitation to Modern Number Theory, Princeton University Press, S. 62.
- ↑ Steven J. Miller, Ramin Takloo-Birhash: An Invitation to Modern Number Theory, Princeton University Press, S. 63.
- ↑ Gerald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Third Edition, S. 265.
- ↑ Norman Levinson: At least One-Third of Zeros of Riemann’s Zeta-Function are on ., Proc. Nat. Acad. Sci. USA, Vol. 71, No. 4, S. 1013–1015.
- ↑ Aleksandar Ivić: The Riemann Zeta-Function. Theory and Applications. Dover Publications Inc., S. 251.
- ↑ Norman Levinson: Deduction of semi-optimal mollifier for obtaining loweer bounds for for Riemann’s zeta-function, Proc. Nat. Acad. Sci. USA, Vol. 72, S. 294–297.
- ↑ Norman Levinson: At least One-Third of Zeros of Riemann’s Zeta-Function are on ., Proc. Nat. Acad. Sci. USA, Vol. 71, No. 4, S. 1013.
- ↑ Shi-Tuo Lou: A lower bound for the number of zeros of Riemann’s zeta-function on , Recent Progress in Analytic Number Theory, Symposium Durham 1979 (Vol. 1), Academic, London, 1981, S. 319–325.
- ↑ Brian Conrey: Zeros of derivatives of the Riemann zeta function on the critical line, J. Number Theory, 16, 1983, S. 49–74.
- ↑ Aleksandar Ivić: The Riemann Zeta-Function. Theory and Applications. Dover Publications Inc., S. 264.
- ↑ Aleksandar Ivić: The Riemann Zeta-Function. Theory and Applications. Dover Publications Inc., S. 264–265.
- ↑ Aleksandar Ivić: The Riemann Zeta-Function. Theory and Applications. Dover Publications Inc., S. 252.
- ↑ J. B. Conrey: More than two fifths of the zeros of the Riemann zeta function are on the critical line. J. Reine Angew. Math. 399 (1989), S. 1–26; doi:10.1515/crll.1989.399.1.
- ↑ Kyle Pratt, Nicolas Robles, Alexandru Zaharescu, Dirk Zeindler: More than five-twelfths of the zeros of are on the critical line. Res Math Sci 7, 2 (2020).
- ↑ F. Mertens: Ueber eine Eigenschaft der Riemann’schen ζ-Function. Wien 1898, S. 1429–1434.
- ↑ Gerald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Third Edition, S. 238.
- ↑ Harold M. Edwards: Riemann’s Zeta Function. Dover, S. 79.
- ↑ a b K. Ford: Vinogradov’s integral and bounds for the Riemann zeta function. In: Proc. London Math. Soc. 85. Jahrgang, Nr. 3, 2002, S. 565–633, doi:10.1112/S0024611502013655 (englisch).
- ↑ Gerald Tenenbaum: Introduction to Analytic and Probabilistic Number Theory, Graduate Studies in Mathematics, American Mathematical Society, Third Edition, S. 252.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 250.
- ↑ W. Ellison, M. Mendès France: Les nombres premiers. Hermann, 1975.
- ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Auflage, Springer, S. 459.
- ↑ Alain Connes: Trace formula in non commutative geometry and the zeros of the Riemann zeta function. 10. November 1998.
- ↑ Gram: Sur les zéros de la fonction de Riemann. In: Acta Mathematica. Band 27, 1903, S. 289–304.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, S. 234
- ↑ Turing, Alan M. (1953), Some calculations of the Riemann zeta-function, Proceedings of the London Mathematical Society, Third Series, 3: S. 99–117.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, S. 238.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, S. 268.
- ↑ Ed Pegg Jr.: «Ten Trillion Zeta Zeros».
- ↑ Gourdon, Xavier (2004): The first zeros of the Riemann Zeta function, and zeros computation at very large height (PDF)
- ↑ Calculations relating to the zeros. Kapitel 15. In: Titchmarsh: The Theory of the Riemann Zeta function.
- ↑ Enrico Bombieri: The Riemann hypothesis. In: J. Carlson, A. Jaffe, und A. Wiles (Hrsg.) The Millennium Prize Problems, Clay Mathematical Institute jointly with the American Mathematical Society, S. 113.
- ↑ Peter Sarnak: Problems of the Millennium: The Riemann Hypothesis ( des vom 13. April 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis., Princeton University & Courant Institute of Math. Sciences, S. 6.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume One: Arithmetic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 164, S. 193.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume One: Arithmetic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 164, S. 167.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume One: Arithmetic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 164, S. 195.
- ↑ a b Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume One: Arithmetic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 164, S. 97.
- ↑ Marcel Riesz: Sur l’hypothèse de Riemann, Acta Mathematica, Band 40, 1916, S. 185–190.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 10.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 20.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 23.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 30.
- ↑ Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, S. 115.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 275–276.
- ↑ Andrew Granville: Refinements of Goldbach’s Conjecture, and the generalized Riemann hypothesis. In: Functiones et Approximatio, Commentarii Mathematici. Band 37, Nr. 1. Faculty of Mathematics and Computer Science of Adam Mickiewicz University, Poznań 2007, S. 159–173.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 323–324.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, S. 6.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, S. 18.
- ↑ Jürgen Neukirch: Algebraische Zahlentheorie. Springer-Verlag, Berlin/Heidelberg 1992, S. 478.
- ↑ Henri Cohen: Number Theory, Volume II. Analytic and Modern Tools. Springer Verlag, S. 217.
- ↑ Peter Sarnak: Problems of the Millennium: The Riemann Hypothesis ( des vom 13. April 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis., Princeton University & Courant Institute of Math. Sciences, S. 2–3.
- ↑ Peter Sarnak: Problems of the Millennium: The Riemann Hypothesis ( des vom 13. April 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis., Princeton University & Courant Institute of Math. Sciences, S. 3.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 178.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 189.
- ↑ Kevin Broughan: Equivalents of the Riemann Hypothesis. Volume Two: Analytic Equivalents. Encyclopedia of Mathematics and Its Applications, Vol. 165, S. 188–189.
- ↑ Große Probleme. In: Spektrum der Wissenschaft, Serie Mathematik (Ausgabe 22. 08. 2008), S. 85.
- ↑ P. Borwein, S. Choi, B. Rooney, A. Weirathmueller: The Riemann hypothesis. A resource for the afficionado and virtuoso alike. (CMS Books in Mathematics 27) Canad. Math. Soc., Springer, 2008, S. 3–4.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, ISBN 978-3-423-34299-5, S. 200.
- ↑ Siehe Prime Suspect – Storyline. In: Imdb, abgerufen am 7. Januar 2022.
- ↑ Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. 5. Auflage. Beck, München 2006, S. 160.
- ↑ Die Riemannsche Vermutung. Von der Schönheit der Primzahlen und den Rätseln der Liebe. Übersetzt von Günther Frauenlob. Piper, München 2007, ISBN 978-3-492-05110-1 (Roten av minus en, 2006).
- ↑ Len Goodman, Eric Weisstein: Riemann Hypothesis. In: MathWorld, abgerufen am 27. März 2022.


































































































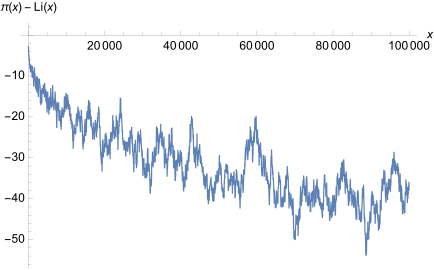
































































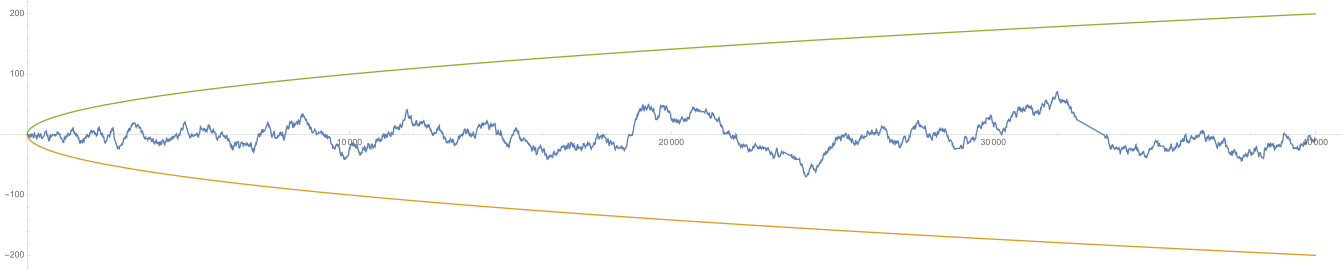



















































































































![{\displaystyle I(s):=\int _{1}^{\infty }{\frac {1}{n^{s}}}\mathrm {d} n=\left[-{\frac {n^{1-s}}{s-1}}\right]_{1}^{\infty }={\frac {1}{s-1}}\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e47e0e7f52784f3db3c4a8734705ab23cfa9c5be)



























































































































































![{\displaystyle [{\tfrac {3}{2}},30]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3866f1e0a0d2598655037b60250afc73f31db8)


































![{\displaystyle [x,x+x^{{\frac {2}{3}}+\varepsilon }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb33be0dccb49c6a28f8928a34ce15e0c59a473d)
![{\displaystyle [x,2x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d77a8feed20f52857ca045fb586e7e93d679880d)







![{\displaystyle 0\in [\alpha ,\beta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcc5fa430cbbc125b8c4d5f9aa14616f44480142)










![{\displaystyle f,g\colon [0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ad6ce3c782a6583e885145ad9ff770df8249ac)






























![{\displaystyle [0,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63d050b0ffe6cc6f635808b9a013366a60e6d0c0)
































































![{\displaystyle [-T,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b8466d3122dfdddcf0f209fc31dd4d3e05e5797)










































![{\displaystyle {\mathcal {M}}:=\left\{f:f(x)=\sum _{n=1}^{N}a_{n}r\left({\frac {\theta _{n}}{x}}\right),a_{n}\in \mathbb {R} ,\theta _{n}\in (0,1],\sum _{n=1}^{N}a_{n}\theta _{n}=0,N\in \mathbb {N} \right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7742686b7460b032fb4cb6af4e5bf4f902d80f7)
































































