Integrallogarithmus

Der Integrallogarithmus ist eine analytische Funktion auf den reellen Zahlen $x\geq 0,\;x\neq 1$ (oder $x>1$) in die reellen Zahlen. Sie hat praktische Relevanz in einigen Gebieten der Physik wie der Quantenfeldtheorie und bei der Lösung der Laplace-Gleichung in Halbleitern sowie in der Zahlentheorie, da sie eng mit der Dichte der Primzahlen verknüpft ist.

Funktionsgraph von $\operatorname {li} (x)$ im Bereich zwischen 0 und 10

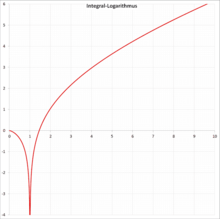
Definition

Es sind zwei Definitionen üblich, die sich um eine Konstante unterscheiden. Für eine der wichtigsten Anwendungen – als asymptotische Vergleichsgröße für die Primzahlfunktion im Primzahlsatz – spielt der Unterschied zwischen den beiden Definitionen keine Rolle.

Eine Definition im Bereich $x\geq 0$ lautet

$\operatorname {li} (x)=\int _{0}^{x}{\frac {\mathrm {d} t}{\ln t}}\ ,$

dabei muss $\operatorname {li}$ wegen der Polstelle bei $x=1$ für $x>1$ über einen Grenzwert definiert werden (cauchyscher Hauptwert):

$\operatorname {li} (x)=\lim _{\varepsilon \to 0^{+}}\left(\int _{0}^{1-\varepsilon }{\frac {\mathrm {d} t}{\ln t}}+\int _{1+\varepsilon }^{x}{\frac {\mathrm {d} t}{\ln t}}\right)\ .$

Eine andere Definition für $x>1$ ist

$\operatorname {Li} (x)=\operatorname {li} (x)-\operatorname {li} (2)=\int _{2}^{x}{\frac {\mathrm {d} t}{\ln t}}\ .$

Bei $x=1$ liegt keine Polstelle, sondern eine logarithmische Singularität vor.

Eigenschaften

Funktionsgraph von $\operatorname {li} (x)$ im Bereich zwischen 0 und 2 (umfasst 0, 1, µ und 2)

Einige Werte:

• $\operatorname {li} (0)=0$
• $\operatorname {li} (1)=-\infty$
• $\operatorname {li} (\mu )=0$
• $\operatorname {li} (2)=1{,}04516\;37801\;17492\;78484\ldots$ (Folge A069284 in OEIS)

Dabei ist $\mu =1{,}45136\;92348\;83381\;05028\ldots$ (Folge A070769 in OEIS) die Ramanujan-Soldner-Konstante.

Es gilt $\operatorname {li} (x)=\operatorname {Ei} (\ln x)$ mit der Integralexponentialfunktion $\operatorname {Ei}$, daraus erhält man die Reihendarstellung

$\operatorname {li} (x)=\gamma +\ln \left|\ln x\right|+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k\cdot k!}}\ ,$

wobei $\gamma =0{,}57721\;56649\;01532\;86060\ldots$ (Folge A001620 in OEIS) die Euler-Mascheroni-Konstante ist.

Aus der Definition von $\operatorname {li}$ erhält man durch lineare Substitution

$\operatorname {li} (x)=x\int _{0}^{1}{\frac {\mathrm {d} t}{\ln(x\,t)}}\ ,$

wobei für $x>1$ wegen der Singularität bei $t=1/x$ der cauchysche Hauptwert eingesetzt werden muss.
Ferner haben wir für $x\geq 0,x\neq 1$

$\int _{0}^{x}\operatorname {li} (t)\,{\mathrm {d} t}=x\,\operatorname {li} (x)-\operatorname {li} (x^{2}).$

Außerdem gilt für $p>-1,p\not =0$

$\int _{0}^{1}\operatorname {li} (t)\,t^{p-1}\,\mathrm {d} t=-{\tfrac {1}{p}}\ln(p+1),$

für $p=1$ erhält man $\textstyle \int _{0}^{1}\operatorname {li} (t)\,\mathrm {d} t=-\ln 2.$
Im Grenzfall $p=0$ ist $\textstyle \int _{0}^{1}\operatorname {li} (t)\,t^{-1}\,\mathrm {d} t=-1.$

Eine weitere Formel ist $\textstyle \int _{0}^{1}\operatorname {li} (t^{-1})\,t\,\mathrm {d} t=\textstyle \int _{1}^{\infty }\operatorname {li} (t)\,t^{-3}\,\mathrm {d} t=0.$

Die Golomb-Dickman-Konstante $\lambda =\textstyle \int _{0}^{1}\mathrm {e} ^{\operatorname {li} (x)}\mathrm {d} x=0{,}62432\;99885\;43550\;87099\ldots$ (Folge A084945 in OEIS) tritt in der Theorie zufälliger Permutationen bei der Abschätzung der Länge des längsten Zykels einer Permutation und in der Zahlentheorie bei der Abschätzung der Größe des größten Primfaktors einer Zahl auf.

Asymptotisches Verhalten

Funktionsgraph von $\operatorname {li} (x)$ im Bereich zwischen 1 und 10¹³

Für große $x$ lässt sich $\operatorname {li} (x)$ durch

$\operatorname {li} (x)=0!\,{\frac {x}{\ln x}}+1!\,{\frac {x}{\ln ^{2}x}}+2!\,{\frac {x}{\ln ^{3}x}}+3!\,{\frac {x}{\ln ^{4}x}}+\dotsb$

approximieren. Die Reihe ist eine asymptotische Entwicklung; sie konvergiert nicht, sondern nähert sich dem wahren Wert an, um sich dann wieder zu entfernen. Die beste Approximation wird nach etwa $\ln x$ Gliedern erreicht, dann werden die Summanden größer durch die stärker werdende Wirkung der Fakultät.

Siehe auch

• Integralsinus
• Integralcosinus

Literatur

• Johann Georg Soldner: Théorie et tables d’une nouvelle fonction transcendante. Lindauer, München 1809 (französisch; bei Google Books)
• Niels Nielsen: Theorie des Integrallogarithmus und verwandter Transzendenten, B. G. Teubner, Leipzig 1906 (archive.org)

Weblinks

• Eric W. Weisstein: Logarithmic Integral. In: MathWorld (englisch).
• Logarithmic integral. bei The Wolfram Functions Site (englisch; mit Berechnungsmöglichkeit)