Irrationale Zahl
Eine irrationale Zahl ist eine reelle Zahl, die keine rationale Zahl ist. Kennzeichen einer irrationalen Zahl ist also, dass sie nicht als Quotient zweier ganzer Zahlen darstellbar ist. In der Dezimalschreibweise werden irrationale Zahlen mit einer nicht periodischen, unendlichen Anzahl von Dezimalstellen dargestellt (z. B. 0,10110111011110…), d. h., sie sind unendliche nichtperiodische Dezimalbrüche.

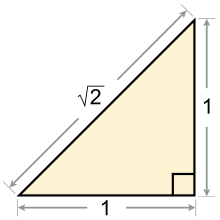
Bekannte irrationale Zahlen sind die Eulersche Zahl und die Kreiszahl , die darüber hinaus transzendent sind. Auch die Quadratwurzel aus Zwei und das Teilungsverhältnis des Goldenen Schnitts sind irrationale Zahlen.
Definition
BearbeitenEine reelle Zahl heißt irrational, wenn sie nicht als Bruch zweier ganzer Zahlen dargestellt werden kann; sie kann nicht als mit geschrieben werden.
Im Gegensatz zu rationalen Zahlen, die als endliche oder periodische Dezimalzahlen dargestellt werden können, sind irrationale Zahlen solche, deren Dezimaldarstellung weder abbricht, noch periodisch ist.
Es gibt zwei Arten von Irrationalzahlen:
- Algebraische Zahlen, etwa oder quadratische Wurzeln aus Nicht-Quadratzahlen wie
- algebraische irrationale Zahlen, die quadratische Gleichungen lösen, nennt man quadratisch irrationale Zahlen
- Transzendente Zahlen, etwa die Kreiszahl oder die Eulersche Zahl
- Weil jede rationale Zahl algebraisch – um genau zu sein, algebraisch vom Grad 1 – ist, ist jede reelle transzendente Zahl irrational.
Die Menge der irrationalen Zahlen lässt sich als Differenzmenge schreiben, wobei die Menge der reellen Zahlen und die Menge der rationalen Zahlen bezeichnet.
Entdeckung der Irrationalität
BearbeitenDen ersten Beweis für irrationale Größenverhältnisse gab es in der griechischen Antike im 5. Jahrhundert v. Chr. bei den Pythagoreern. Definitionen für irrationale Zahlen, die den heutigen Ansprüchen an Exaktheit genügen, finden sich bereits in den Elementen von Euklid. Übersetzungen in die heutige Sprache der Mathematik gaben zuerst Karl Weierstraß und Richard Dedekind an.[2]
Hat man ein Quadrat mit der Seitenlänge und berechnet dessen Diagonale , folgt aus dem Satz des Pythagoras also . Die positive Lösung dieser Gleichung bezeichnet man heute mit . Für griechische Mathematiker stellte sich die Frage, ob sich die Länge dieser Diagonalen exakt durch ein Verhältnis zweier natürlicher Zahlen und , also einen Bruch , darstellen lässt. Schon Euklid bewies durch Widerspruch, dass dies unmöglich ist; sein Beweis wird heute noch in der Schule gelehrt. Ob die Entdeckung der Irrationalität durch Anwendung des pythagoräischen Lehrsatzes auf ein Quadrat erfolgte oder, wie Kurt von Fritz meinte, durch stetige Teilung am Pentagramm, ist unbekannt.[3]
Die ältere wissenschaftsgeschichtliche Forschung nahm an, dass die Entdeckung der Irrationalität zu einer Grundlagenkrise der damaligen griechischen Mathematik oder der pythagoreischen Zahlenlehre führte. Man sei nämlich vorher von der Grundvoraussetzung ausgegangen, dass alles durch ganzzahlige Zahlverhältnisse ausdrückbar sei, und die Widerlegung dieser Ansicht habe das Weltbild der Pythagoreer erschüttert. Damit wurde eine antike Legende in Zusammenhang gebracht, wonach der Pythagoreer Hippasos von Metapont im 5. Jahrhundert v. Chr. durch die schriftliche Bekanntmachung dieser Entdeckung einen Geheimnisverrat begangen habe und später im Meer ertrunken sei, was als göttliche Strafe gedeutet wurde. Ein Teil der Quellen überliefert, Hippasos selbst habe die Irrationalität entdeckt. Wissenschaftshistoriker gehen heute davon aus, dass es eine solche Krise nicht gegeben hat und die Irrationalität nicht als Geheimnis betrachtet wurde. Eine mögliche Erklärung der Verratslegende ist, dass sie durch ein Missverständnis entstand, weil das griechische Eigenschaftswort, das für „irrational“ (im mathematischen Sinn) verwendet wurde, zugleich die Bedeutungen „unsagbar“ und „geheim“ hatte.[4] Tatsache ist aber auch, dass sich die griechische Mathematik in der Zeit nach Hippasos grundlegend veränderte.
Zahlen, deren Irrationalität bewiesen ist
Bearbeiten- Schon der Pythagoreer Archytas von Tarent bewies die Irrationalität von für natürliche Zahlen . Der Beweis für den Fall ( ) ist in Euklids Elementen überliefert (Euklids Beweis der Irrationalität der Wurzel aus 2). Den Satz des Archytas verallgemeinerte Euklid selbst in seiner Musiktheorie, in der er die Irrationalität beliebiger Wurzeln bewies.
- Eine weitere wichtige quadratische Irrationalität ist der Goldene Schnitt .
- Die Eulersche Zahl ist irrational. Dies wurde von Leonhard Euler 1737 bewiesen. Ihre Transzendenz wurde 1873 von Charles Hermite bewiesen.
- 1761 bewies Johann Heinrich Lambert die Irrationalität der Kreiszahl , ihre Transzendenz wurde 1882 von Ferdinand von Lindemann bewiesen.
- Die nichtganzzahligen Nullstellen eines normierten Polynomes mit ganzzahligen Koeffizienten sind irrational. Insbesondere sind die Quadratwurzeln aus Nichtquadratzahlen irrational.
- Im Jahr 1979 bewies Roger Apéry die Irrationalität der Apéry-Konstante .[5]
- ist für jede algebraische Zahl transzendent (siehe Satz von Lindemann-Weierstraß)
- ist transzendent (siehe Satz von Gelfond-Schneider).
- ist transzendent, dies hat Carl Ludwig Siegel bewiesen.
- Die Transzendenz und damit die Irrationalität von (wie auch von ) folgen aus dem Satz von Gelfond-Schneider.
- Die lemniskatische Konstante ist transzendent (Theodor Schneider, 1937).
- Im Jahr 1963 bewies Solomon W. Golomb die Irrationalität der Summe der Reziproken aller Fermat-Zahlen.[6] Es gilt:
- Alle liouvilleschen Zahlen sind transzendent und damit irrational.
- ist für jede rationale Zahl stets irrational, was wiederum wegen der Rationalität von die Irrationalität von nach sich zieht.[7]
- Überdies ist nach dem Satz von Lindemann-Weierstraß für jede algebraische (und damit auch für jede rationale) Zahl transzendent.
- Bewiesen ist ebenfalls, dass als transzendente Zahl irrational ist, während die Irrationalität von fraglich ist.[8]
Zahlen, deren Irrationalität vermutet wird
Bearbeiten- Die Irrationalität der Zahlen wird vermutet, ist aber noch nicht bewiesen. Man kann aber leicht sehen, dass mindestens eine von einer beliebigen Paarbildung irrational sein muss. Dies gilt allgemein für zwei beliebige transzendente Zahlen und
- Für kein einziges Paar ganzer, von verschiedener Zahlen und ist bekannt, ob irrational ist. Bekannt ist jedoch, dass im Falle der Existenz rationaler Linearkombinationen der Wert einen konstanten Wert annimmt.
- Weiterhin ist unbekannt, ob , , , , , die Catalansche Konstante oder die Euler-Mascheroni-Konstante irrational sind.
Die Überabzählbarkeit der irrationalen Zahlen
BearbeitenWie das erste Diagonalargument von Cantor zeigt, ist die Menge der rationalen Zahlen abzählbar. Es gibt also eine Folge rationaler Zahlen, die jede rationale Zahl enthält. Cantors zweites Diagonalargument beweist, dass es überabzählbar viele reelle Zahlen gibt. Das bedeutet gleichzeitig, dass es überabzählbar viele irrationale Zahlen geben muss;[9] denn andernfalls wären die reellen Zahlen als Vereinigung zweier abzählbarer Mengen selbst abzählbar.
Cantor hat weiter gezeigt, dass auch die Menge der algebraischen Zahlen, wozu alle Wurzelausdrücke gehören, noch abzählbar ist. Darüber hinaus gilt, dass die algebraische Hülle jeder abzählbaren Teilmenge der reellen oder komplexen Zahlen (solche Mengen können insbesondere aus transzendenten Zahlen bestehen) ebenfalls abzählbar ist, also sicher nicht alle reellen Zahlen enthält.
Literatur
Bearbeiten- Peter Bundschuh: Einführung in die Zahlentheorie (= Springer-Lehrbuch). 6., überarbeitete und aktualisierte Auflage. Springer Verlag, Berlin / Heidelberg 2008, ISBN 978-3-540-76490-8.
- John H. Conway, Richard K. Guy: Zahlenzauber: Von natürlichen, imaginären und anderen Zahlen. Aus dem Amerikan. von Manfred Stern. Springer Basel AG, Basel 1967, ISBN 978-3-0348-6085-7, doi:10.1007/978-3-0348-6084-0.
- Steven R. Finch: Mathematical Constants (= Encyclopedia of Mathematics and its Applications. Band 94). Cambridge University Press, Cambridge [u. a.] 2003, ISBN 0-521-81805-2.
- Tom Müller: Irrationalitätsbeweise (= Berliner Studienreihe zur Mathematik. Band 25). Heldermann Verlag, Lemgo 2014, ISBN 978-3-88538-125-9.
- Oskar Perron: Irrationalzahlen (= Göschens Lehrbücherei, I. Gruppe. Band 1). 4., durchgesehene und ergänzte Auflage. Walter de Gruyter & Co., Berlin 1960.
- Harald Scheid: Zahlentheorie. 3. Auflage. Spektrum Akademischer Verlag, Heidelberg / Berlin 2003, ISBN 3-8274-1365-6.
- Carl Ludwig Siegel: Transzendente Zahlen. Übersetzung aus dem Englischen von B. Fuchssteiner und D. Laugwitz (= BI-Hochschultaschenbücher. Band 137*). Bibliographisches Institut, Mannheim 1967.
Weblinks
BearbeitenEinzelnachweise
Bearbeiten- ↑ Für die Menge der irrationalen Zahlen gibt es kein eigenes Kürzel, aber eine Zahl ist genau dann irrational, wenn sie reell und nicht rational ist. Es gilt also:
Menge der irrationalen Zahlen := Menge der reellen Zahlen ohne Menge der rationalen Zahlen. - ↑ Lucio Russo: Die vergessene Revolution oder die Wiedergeburt des antiken Wissens. Springer, Berlin / Heidelberg / New York 2005, ISBN 978-3-540-20938-6, S. 53–56.
- ↑ Walter Burkert: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon. Carl, Nürnberg 1962, S. 430–440.
- ↑ Walter Burkert: Weisheit und Wissenschaft. Studien zu Pythagoras, Philolaos und Platon. Carl, Nürnberg 1962, S. 436 f.
- ↑ Roger Apéry: Irrationalité de ζ (2) et ζ (3). In: Astérisque. Nr. 61, 1979, S. 11–13.
- ↑ Solomon W. Golomb: On the sum of the reciprocals of the Fermat numbers and related irrationalities. Canad. J. Math., Vol. 15, 1963, S. 475–478, archiviert vom am 21. März 2016; abgerufen am 9. August 2016.
- ↑ Carl Ludwig Siegel: Transzendente Zahlen (= BI-Hochschultaschenbücher. Band 137*). Bibliographisches Institut, Mannheim 1967, S. 18.
- ↑ Carl Ludwig Siegel: Transzendente Zahlen (= BI-Hochschultaschenbücher. Band 137*). Bibliographisches Institut, Mannheim 1967, S. 81.
- ↑ Das bedeutet insbesondere, dass sich nicht alle irrationalen Zahlen „darstellen“ oder „berechnen“ lassen.



