Rationale Funktion
Eine rationale Funktion ist in der Mathematik eine Funktion, die als Quotient zweier Polynomfunktionen darstellbar ist. Sie hat also die Form
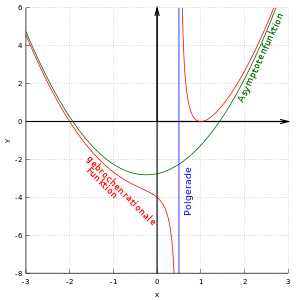
blau: Polgerade durch die Polstelle bei
grün: Asymptotenfunktion , stetig behebbare Definitionslücke bei
mit natürlichen Zahlen und . Die Zahlen können beliebige reelle Zahlen (oder auch komplexe Zahlen) sein; die einzige Einschränkung ist, dass sein muss. Die höchsten Koeffizienten und sollen nicht Null sein.
Abstrakter kann man für die Koeffizienten Elemente eines beliebigen Körpers zulassen. Die rationalen Funktionen mit komplexen Koeffizienten gehören zu den meromorphen Funktionen.
Allgemeiner kann man rationale Funktionen in mehreren Variablen sowie rationale Funktionen auf algebraischen Varietäten über beliebigen Körpern betrachten.
Einteilung
Bearbeiten- Ist das Nennerpolynom vom Grad , also konstant, so spricht man von einer ganzrationalen Funktion oder von einer Polynomfunktion.
- Kann man den Funktionsterm ausschließlich mit einem Nennerpolynom vom Grad darstellen, so handelt es sich um eine gebrochenrationale Funktion.
- Ist und , so handelt es sich um eine echt gebrochenrationale Funktion.
- Ist und , so handelt es sich um eine unecht gebrochenrationale Funktion. Sie kann über Polynomdivision in eine ganzrationale Funktion und eine echt gebrochenrationale Funktion aufgeteilt werden (siehe unten).
Beispiele für rationale Funktionen mit unterschiedlichen Zählergraden und Nennergraden :
| Beispiel | alternative Schreibweise | m = | n = | Funktionstyp |
|---|---|---|---|---|
| 3 | 0 | ganzrational | ||
| 1 | 2 | echt gebrochenrational | ||
| 3 | 3 | unecht gebrochenrational | ||
| 2 | 1 | unecht gebrochenrational |
Kurvendiskussion
BearbeitenAnhand des Funktionsterms der rationalen Funktion lassen sich folgende Aussagen zum Funktionsgraphen machen (Kurvendiskussion).
Definitionsbereich, Nullstellen und Polstellen
BearbeitenDie gebrochenrationale Funktion ist an den Nullstellen der Nennerfunktion nicht definiert.
Die Nullstellen einer gebrochenrationalen Funktion werden durch diejenigen Nullstellen der Zählerfunktion bestimmt, die zum Definitionsbereich der gesamten Funktion gehören.
Ein Spezialfall ergibt sich, wenn eine reelle Zahl gleichzeitig Nullstelle des Zählerpolynoms und des Nennerpolynoms ist. Dann sind Zähler- und Nennerpolynom durch den zugehörigen Linearfaktor (eventuell sogar mehrfach) teilbar, das heißt, der Funktionsterm kann mit diesem Faktor (eventuell mehrfach) gekürzt werden.
- Kommt im Nenner -mal öfter vor als im Zähler (mit natürlicher Zahl , ), so liegt eine Polstelle vor ( heißt dann die Vielfachheit der Polstelle);
- andernfalls hat die rationale Funktion an der Stelle eine stetig hebbare Definitionslücke, und man kann die Funktion stetig fortsetzen
Beispiele:
- Die Funktion hat den Definitionsbereich , da die Nennerfunktion die Nullstelle hat, und die Nullstelle , da das die einzige Nullstelle der Zählerfunktion ist (und zu gehört). ist eine (doppelte) Polstelle.
- Die Funktion hat den Definitionsbereich . Hier ist aber nun eine Nullstelle der Zähler- und der Nennerfunktion. Um den entsprechenden Linearfaktor zu kürzen, faktorisiert man Zähler und Nenner zunächst (durch Ausklammern bzw. Anwenden der binomischen Formeln); das führt auf bzw. nach kürzen auf . Damit ergibt sich: ist eine (einfache) Polstelle, dagegen eine stetig behebbare Definitionslücke von , und hat die Nullstelle (beachte: ist keine Nullstelle von , da dieser Wert nicht zu gehört!). Für die stetige Fortsetzung von ergibt sich: und .
Asymptotisches Verhalten
BearbeitenFür das Verhalten für gegen Unendlich sind die Grade bzw. des Zähler- bzw. Nennerpolynoms entscheidend:
Für geht
- (Fall 1) gegen , falls , wobei die Vorzeichenfunktion darstellt.
- (Fall 2) gegen , falls (die Asymptote ist parallel zur -Achse),
- (Fall 3) gegen (die -Achse ist waagrechte Asymptote), falls ,
Für ergibt sich in den Fällen 2 und 3 jeweils derselbe Grenzwert wie für . Im Fall 1 muss man Zähler- und Nennergrad noch genauer berücksichtigen:
- Ist gerade, so ergibt sich derselbe Grenzwert wie für .
- Ist ungerade, so ändert sich im Vergleich zu das Vorzeichen des Grenzwerts.
Beispiele:
- Bei der gebrochenrationalen Funktion ist der Zählergrad und der Nennergrad , der Grenzwert für ist also .
- Die gebrochenrationale Funktion hat den Zählergrad und auch den Nennergrad ; da hier und ist, ergibt sich für die Gleichung der waagrechten Asymptote: .
- Die gebrochenrationale Funktion hat den Zählergrad und den Nennergrad ; mit den Koeffizienten und ergibt sich also: für . Da hier ungerade ist, folgt für den Grenzwert für das umgedrehte Vorzeichen, also . Diese Funktion kann man auch schreiben als , das heißt, die (schräge) Asymptote hat die Gleichung (und daraus ergibt sich auch leicht wieder das eben geschilderte Grenzverhalten).
Untersuchung mit Polynomdivision
Im oben genannten Fall 1 ( ) kann man den Funktionsterm mittels Polynomdivision in eine Summe aus einem Polynom und einem echt gebrochenrationalen Term zerlegen; das Polynom beschreibt dann eine sogenannte Asymptotenkurve. Das oben beschriebene Verhalten der Funktionswerte für kann man auch einfacher erhalten, indem man nur das Verhalten dieser Asymptotenkurve untersucht. Im Sonderfall ergibt sich eine schräg verlaufende Asymptote.
Wie oben stehen für den Grad des Zählerpolynoms und für den Grad des Nennerpolynoms . Es werden wieder alle Fälle betrachtet (nicht nur ).
Mittels Polynomdivision von durch erhält man zunächst eine Darstellung
mit Polynomen und , wobei der Grad von echt größer als der von ist. Daraus folgt die nützliche Gleichung
- .
Das asymptotische Verhalten von ist nun dasselbe asymptotische Verhalten der ganzrationalen Funktion („Asymptotenfunktion“) . Der Quotient spielt keine Rolle.
Wenn man sich die Mühe der Polynomdivision gemacht hat und die oben beschriebene nützliche Gleichung aufstellt, tut man sich mit der Fallunterscheidung leichter. Es gilt:
Fall 1: → -Achse ist Asymptote:
Fall 2: → waagerechte Asymptote:
Fall 3: → schräge Asymptote: mit und
Fall 4: → ist ein Polynom vom Grad ; der Leitkoeffizient dieses Polynoms ist gleich .
Symmetrie
BearbeitenEine Polynomfunktion (ganzrationale Funktion) ist gerade/ungerade, wenn alle Exponenten gerade/ungerade sind. Sind Zählerpolynom und Nennerpolynom von einem dieser beiden Typen, so ist auch die rationale Funktion gerade oder ungerade:
- Sind und beide gerade oder beide ungerade, so ist gerade (d. h. der Graph ist symmetrisch zur y-Achse)
- Ist gerade und ungerade, so ist ungerade (d. h. der Graph ist punktsymmetrisch zum Ursprung); gleiches gilt, wenn ungerade und gerade ist.
In allen anderen Fällen, wenn also Zähler- oder Nennerfunktion oder beide weder gerade noch ungerade sind, sind Symmetrieeigenschaften von schwieriger zu entscheiden. (Siehe auch Kurvendiskussion und Symmetrie in der Geometrie).
Beispiele:
- Der Graph zur Funktion mit ist symmetrisch zum Ursprung, da ungerade und gerade, die Funktion insgesamt also ungerade ist.
- Der Graph zur Funktion ist symmetrisch zur y-Achse, da und beide ungerade, die Funktion insgesamt also gerade ist. Das kann man auch anders sehen: Klammert man in Zähler und Nenner jeweils x aus, kann man den Funktionsterm kürzen zu ; nun sind und gerade, die Funktion insgesamt also wiederum gerade.
- Beim Graph zur Funktion mit dem Term ist zunächst keine Symmetrie erkennbar ( ist ungerade, aber weder gerade noch ungerade); man kann aber zeigen, dass der Graph symmetrisch zum Punkt P(1|1) ist; es gilt nämlich:
- und
- ,
- also insgesamt: , was eben gerade Symmetrie zum Punkt P(1|1) bedeutet. Alternativ kann man auch zeigen, dass der Graph von aus dem Graph der Funktion (welcher symmetrisch zum Ursprung ist) durch Verschieben um 1 in -Richtung und um 1 in -Richtung hervorgeht.
Ableitung
BearbeitenZum Ableiten gebrochenrationaler Funktionen muss man im Allgemeinen die Quotientenregel verwenden; zusätzlich kann auch oft die Kettenregel nützlich sein, beispielsweise wenn die Nennerfunktion eine Potenz eines Binoms ist. Vor dem Ableiten empfiehlt es sich oft, den Funktionsterm zunächst mit Hilfe einer Polynomdivision umzuschreiben und den übrigbleibenden echt gebrochenrationalen Term zu kürzen.
Beispiele:
- Bei der Funktion ist es sinnvoll, neben der Quotientenregel auch die Kettenregel anzuwenden, statt zunächst im Nenner die erste binomische Formel anzuwenden. Mit der Kettenregel ergibt sich zunächst für die Ableitung der Nennerfunktion (in der Quotientenregel meist mit bezeichnet):
- ,
- und damit insgesamt für die Ableitungsfunktion von :
- .
- Nun kann man im Zähler einen Faktor ausklammern und kürzen:
- .
- Vereinfachen des Zählers führt schließlich auf
- .
- Den Funktionsterm bringt man mit Hilfe einer Polynomdivision zunächst auf die Form
- ,
- woran man auch gleich die Gleichung der schrägen Asymptote ablesen kann:
- .
- Faktorisieren von Zähler und Nenner führt dann auf
- ,
- man kann also einen Faktor kürzen. Schließlich hat man:
- ;
- in dieser Form kann man die Funktion nun deutlich leichter ableiten als in der ursprünglich gegebenen.
- Mit Hilfe der Quotientenregel ergibt sich:
- .
- Setzt man die erste Ableitung gleich Null, um die Extremstellen zu suchen, so empfiehlt es sich vorher, die beiden Brüche wieder zusammenzufassen:
- .
Stammfunktion
BearbeitenIm Gegensatz zu den ganzrationalen Funktionen ist es bei gebrochenrationalen Funktionen oft relativ schwierig, eine Stammfunktion zu finden. Dafür kann man, je nach Form der gebrochenrationalen Funktion, unter anderem folgende Regeln anwenden (meist muss man den Funktionsterm durch Umformungen und/oder Substitution zunächst in eine passende Form bringen):
- für
- für
- oder
- für
- für
- für
Oft kann für die Bestimmung einer Stammfunktion auch die Partialbruchzerlegung hilfreich sein. Beispiele:
- Gesucht sei eine Stammfunktion zu . Mittels einer Polynomdivision kann man das zunächst umschreiben zu:
- .
- Anwenden der ersten Regel liefert dann als mögliche Stammfunktion:
- .
- Gesucht sei eine Stammfunktion zu , wobei zwischen −0,5 und 0,5 liegen soll. Wieder kann man den Funktionsterm zunächst mittels einer Polynomdivision umschreiben:
- .
- Anwenden der vierten Regel liefert dann als mögliche Stammfunktion:
- .
- Gesucht sei eine Stammfunktion zu . Das kann auch geschrieben werden als
- mit .
- Anwenden der letzten Regel liefert dann als mögliche Stammfunktion:
- .
- Eine Stammfunktion zu kann man mit Hilfe der Substitution bestimmen, nachdem man den Nenner mittels quadratischer Ergänzung umgeformt hat:
- Eine Stammfunktion zu kann man mit Hilfe der Partialbruchzerlegung erhalten, nachdem man den Nenner zunächst faktorisiert hat:
Rationale Funktionen in mehreren Variablen
BearbeitenEine rationale Funktion in Variablen ist eine Funktion der Form , wobei und Polynome in den Unbestimmten sind und .
Beispiele
BearbeitenStetigkeit
BearbeitenDer Definitionsbereich von besteht aus denjenigen Punkten , die entweder keine Nullstelle von sind oder deren Vielfachheit als Nullstelle von mindestens so groß ist wie die Vielfachheit als Nullstelle von . Rationale Funktionen sind in allen Punkten ihres Definitionsbereiches stetig.
Anwendungen
BearbeitenRationale Funktionen haben vielfältige Anwendungen in Naturwissenschaften und Technik:
- Viele Größen sind umgekehrt proportional zueinander, eine der Größen ist also eine rationale Funktion der anderen, wobei der Zähler konstant und der Nenner eine (homogene) lineare Funktion ist. Einige wenige Beispiele:
- Die Geschwindigkeit und die für eine feste Strecke benötigte Zeit sind umgekehrt proportional zueinander:
- Die Konzentration eines Stoffes ist bei fester Stoffmenge umgekehrt proportional zum Volumen des Lösungsmittels:
- Beschleunigung und Masse sind bei fester Kraft umgekehrt proportional zueinander: .
- Für die Kapazität eines Plattenkondensators gilt in Abhängigkeit vom Plattenabstand : mit dem Flächeninhalt der Platten, der elektrischen Feldkonstante und der Permittivität .
- In vielen Bereichen der Physik kommen Funktionen von zwei Variablen und der folgenden Form vor: . Ist eine der beiden Variablen, z. B. , konstant oder wählt man sie als Parameter, so ergibt sich eine rationale Funktion (bzw. Funktionenschar) von . Solche Funktionen treten immer dann auf, wenn sich der gesamte Kehrwert irgendeiner Größe als Summe oder Differenz der Kehrwerte zweier anderer Funktionen ergibt.
- Mittels der Linsengleichung der Optik kann man die Brennweite als Funktion von Gegenstandsweite und Bildweite darstellen: ; umstellen nach oder liefern eine sehr ähnliche Funktion, allerdings mit - statt mit +.
- Für den Gesamtwiderstand einer Parallelschaltung zweier Widerstände und ergibt sich: ; eine analoge Formel gilt bei der Reihenschaltung zweier Kondensatoren.
- In der Mechanik ergibt sich, wenn man zwei Federn mit Federkonstanten und aneinander hängt, für die gesamte Federkonstante der Anordnung:
- Bei einem Spannungsteiler ist die gesamte an einem Widerstand abfallende Spannung gegeben durch: , wobei die zu teilende Spannung und der andere Widerstand ist.
- Für die elektrische Leistung , die ein Gerät mit Widerstand erbringt, das an einer Spannungsquelle (Spannung ) mit Innenwiderstand angeschlossen ist, ergibt sich: . Die größtmögliche Leistung (zu bestimmen mit Hilfe der Differenzialrechnung) erhält man also dann, wenn ist (Leistungsanpassung).
- Für die Induktivität einer (nicht zu kurzen) Spule in Abhängigkeit von ihrem Radius gilt: . Dabei ist die Länge der Spule (man kann also auch als rationale Funktion von auffassen), die Windungszahl und die magnetische Feldkonstante.
- Die Bremskraft einer Wirbelstrombremse hängt folgendermaßen von der Geschwindigkeit ab: mit Konstanten und .
- Bei der Atwoodschen Maschine hängt die Beschleunigung folgendermaßen von den beiden Massen und ab: ; man kann also als rationale Funktion sowohl von als auch von auffassen.
- Auch geometrische Fragestellungen führen oft auf rationale Funktionen. Beispiel: Bei einer Truhe, die aus einem Quader (Grundseitenlängen und , Höhe ) mit aufgesetztem Halb-Zylinder (Höhe , Radius ) besteht, gilt für den Oberflächeninhalt in Abhängigkeit von bei gegebenem Volumen : .
Abweichende Bedeutung in der abstrakten Algebra
BearbeitenRationale Funktionen über einem beliebigen Körper
BearbeitenIn der abstrakten Algebra wird der Begriff einer rationalen Funktion in einem allgemeineren und etwas unterschiedlichen Sinne verwendet. Und zwar versteht man unter einer rationalen Funktion in Variablen über einem Körper ein Element des Quotientenkörpers des Polynomrings . Dieser Quotientenkörper wird Rationaler Funktionenkörper genannt.
Im Allgemeinen ist eine rationale Funktion also keine Funktion irgendeiner Art, sondern ein (formaler) Bruch aus zwei Polynomen. Die Umkehrung muss nicht gelten, der Unterschied macht sich allerdings nur über endlichen Körpern bemerkbar: So ist z. B. für jede Primzahl über dem endlichen Körper (dem Körper aller Restklassen ganzer Zahlen modulo ) der Bruch eine wohldefinierte rationale Funktion in der Variablen , aber keine Funktion im eigentlichen Sinne des Begriffes, weil man in diese Funktion keinen einzigen Wert einsetzen darf, ohne dass der Nenner 0 wird. (Denn setzt man irgendein in diese „Funktion“ ein, erhält man , was undefiniert ist, weil der Nenner nach dem kleinen Fermatschen Satz gleich 0 ist.) Über unendlichen Körpern allerdings ist eine rationale Funktion immer eine Funktion, die zwar eine Definitionslücke haben kann, aber diese Definitionslücke ist nur sehr klein im Vergleich zum Definitionsbereich. Dieser Gedanke wird mit dem Begriff der Zariski-Topologie formalisiert: Die Definitionslücke ist eine Zariski-abgeschlossene Menge, und die abgeschlossene Hülle des Definitionsbereiches ist die ganze Menge.
Rationale Funktionen auf einer algebraischen Varietät
BearbeitenSei eine algebraische Varietät definiert durch Polynome , also
Sei
Der Ring der ganzen Funktionen ist . Der Körper der rationalen Funktionen ist der Quotientenkörper des Ringes der ganzen Funktionen.
Allgemeiner gibt es den Begriff rationaler Abbildungen zwischen (quasi-projektiven) Varietäten. Rationale Funktionen sind der Spezialfall rationaler Abbildungen von einer Varietät nach .
Weblinks
Bearbeiten- Rationale Funktionen - Ein Digitales Lehrbuch © 2000 - 2001 by Henning Koch










