Kurvendiskussion

Unter Kurvendiskussion versteht man in der Mathematik die Untersuchung des Graphen einer Funktion auf dessen geometrische Eigenschaften, wie zum Beispiel Schnittpunkte mit den Koordinatenachsen, Hoch- und Tiefpunkte, Wendepunkte, gegebenenfalls Sattel- und Flachpunkte, Asymptoten, Verhalten im Unendlichen usw. Diese Informationen erlauben es, eine Skizze des Graphen anzufertigen, aus der all diese für die Funktion charakteristischen Eigenschaften unmittelbar ablesbar sind.

Abb. 1: Plot der Funktion f im Ausschnitt:
−1 < x < 5,
0 < y < 12

Abb. 2: Plot der Funktion f im Ausschnitt:
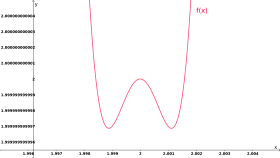
1,995 < x < 2,005,
1,999999999995 < y < 2,000000000005

Es ist heute hingegen nicht mehr das Ziel einer Kurvendiskussion, den Menschen dabei zu unterstützen, eine möglichst genaue Zeichnung des Graphen der Funktion zu produzieren: das kann inzwischen jeder Funktionsplotter (etwa ein grafikfähiger Taschenrechner, ein Smartphone mit entsprechender Software, ein Tabellenkalkulationsprogramm oder Computeralgebra-Software) besser.

Ziel der Kurvendiskussion ist vielmehr,

• die Koordinaten der charakteristischen Punkte des Graphen exakt zu bestimmen (aus einem Funktionsplot lassen sich lediglich ungefähre Werte ablesen);
• charakteristische Eigenschaften wie Symmetrie oder Verhalten im Unendlichen zu beweisen. Aus einem Funktionsplot kann man immer nur Aussagen über den abgebildeten Ausschnitt des Koordinatensystems ablesen, z. B. für den Bereich $-6\leq x\leq 6$, $-4\leq y\leq 10$. Ob der Graph einer Funktion aber z. B. bei $x=10.000$ noch einmal einen „Schlenker“ macht oder nicht, darüber kann nur auf der Grundlage einer Kurvendiskussion eine zuverlässige Aussage getroffen werden.
• genauer hinzusehen: ein augenscheinliches globales Minimum kann sich – bei entsprechender Vergrößerung – als ein lokales Maximum herausstellen. Man vergleiche etwa die beiden Plots der Funktion

$f(x)=2\cdot (x-2)^{4}-0{,}000005\cdot (x-2)^{2}+2$

in Abbildung 1 bzw. Abbildung 2. Eine Kurvendiskussion deckt solche Phänomene stets auf, ob sie sich im Molekülbereich oder in astronomischen Dimensionen abspielen: weil eine Kurvendiskussion nicht – wie ein Funktionsplot – von der Auflösung abhängt.

Zudem lässt sich eine Kurvendiskussion auch ganz ähnlich bei Funktionen durchführen, die von vielen Variablen abhängen (also z. B. von $x_{1}$, $x_{2}$ und $x_{3}$ anstelle von nur $x$). Eine zwei- oder dreidimensionale Visualisierung einer derartigen Funktion ist nicht mehr möglich.

Die Bedeutung der Kurvendiskussion wird auch deutlich vor dem Hintergrund, dass in entscheidungsunterstützenden Systemen Hoch- bzw. Tiefpunkte automatisch, d. h. ohne Benutzerinteraktion, zu berechnen sind. Soll beispielsweise die Auswirkung der Veränderung einer Randbedingung auf die zu optimierende Größe untersucht werden, so würde solch ein System den jeweiligen Extremwert anzeigen bzw. grafisch visualisieren, während ein Wert, der die Randbedingung beschreibt (etwa die Höhe einer Ressource), variiert wird.

Definitionsbereich

Bei einer Kurvendiskussion wird fast immer die Menge $\mathbb {R}$ aller reellen Zahlen als Grundmenge vorausgesetzt. Der maximale Definitionsbereich einer Funktion $f$ ist also die Menge aller reellen Zahlen $x$, für die der Funktionswert $f(x)$ definiert ist. Für ganzrationale Funktionen (Polynomfunktionen) ist der maximale Definitionsbereich gleich $\mathbb {R}$. Bei gebrochenrationalen Funktionen gehören alle reellen Zahlen mit Ausnahme der Nullstellen des Nenners zum maximalen Definitionsbereich.

Beispiele:

• $f(x)={\frac {1}{x(x-3)}};\quad D=\mathbb {R} \setminus \{0;3\}$

Der Nenner des Bruchs darf nicht gleich 0 sein. Daher sind die $x$-Werte 0 und 3 ausgeschlossen.

• $f(x)={\sqrt {25-x^{2}}};\quad D=\{x\in \mathbb {R} |-5\leq x\leq 5\}=[-5;5]$

Der Radikand, also der Rechenausdruck unter der Quadratwurzel, muss größer oder gleich 0 sein. Diese Bedingung ist genau für die Zahlen erfüllt, deren Betrag kleiner oder gleich 5 ist.

• $f(x)=\ln(x+4);\quad D=\{x\in \mathbb {R} |x>-4\}=\left]-4;\infty \right[$

Die natürliche Logarithmusfunktion $\ln$ ist nur für positive Argumente definiert. Also muss $x>-4$ gelten.

Schnittpunkte mit den Koordinatenachsen

Um die Nullstellen einer Funktion $f$ und damit die Schnittpunkte des Funktionsgraphen mit der $x$-Achse zu finden, wird die Lösungsmenge der Gleichung $f(x)=0$ berechnet. Die genaue Vorgehensweise hängt davon ab, welche Funktion untersucht wird. Ist die Funktion $f$ beispielsweise durch einen Bruchterm gegeben, so wird der Zähler gleich 0 gesetzt, um die Nullstellen zu erhalten.

Um den Schnittpunkt des Funktionsgraphen mit der $y$-Achse zu bestimmen, wird für $x$ der Wert 0 eingesetzt. Der y-Achsenabschnitt liegt dann folglich bei $(0|f(0))$.

Symmetrieeigenschaften

Bei der Beantwortung der Frage, ob der Graph der gegebenen Funktion in irgendeiner Weise symmetrisch ist, müssen mehrere Fälle berücksichtigt werden.

Achsensymmetrie bezüglich der y-Achse

• Der Graph einer Funktion $f$ ist genau dann achsensymmetrisch bezüglich der $y$-Achse, wenn für beliebige $x$-Werte des Definitionsbereiches gilt:

$f(-x)=f(x)$

Bei ganzrationalen Funktionen bedeutet diese Bedingung, dass nur gerade Exponenten auftreten.

Punktsymmetrie bezüglich des Ursprungs

• Der Graph einer Funktion $f$ ist genau dann punktsymmetrisch bezüglich des Ursprungs, wenn für beliebige $x$-Werte des Definitionsbereiches gilt:

$f(-x)=-f(x)$

Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch bezüglich des Ursprungs, wenn nur ungerade Exponenten vorkommen.

Achsensymmetrie bezüglich einer beliebigen Achse

• Achsensymmetrie in Bezug auf die Gerade mit der Gleichung $x=x_{0}$ (parallel zur $y$-Achse) lässt sich überprüfen mithilfe der Bedingung

$f(x_{0}-h)=f(x_{0}+h).$

Achsensymmetrisch sind unter anderem die Graphen der quadratischen Funktionen. Die Symmetrieachse ergibt sich in diesem Fall aus der $x$-Koordinate des (Parabel-)Scheitels.

Punktsymmetrie bezüglich eines beliebigen Zentrums

• Die Bedingung für Punktsymmetrie bezüglich des Punktes $(x_{0}|y_{0})$ lautet

$f(x_{0}-h)+f(x_{0}+h)=2y_{0}$

oder (äquivalent)

$f(x_{0}+h)-y_{0}=y_{0}-f(x_{0}-h).$

Die Graphen aller kubischen Funktionen sind punktsymmetrisch. Symmetriezentrum ist jeweils der (einzige) Wendepunkt (siehe unten).

Extrempunkte

→ Hauptartikel: Extrempunkt

Um die Extrempunkte – das heißt Hoch- und Tiefpunkte – einer stetig differenzierbaren Funktion $f$ zu bestimmen, wird die erste Ableitung von $f$ gleich 0 gesetzt, das heißt, die Lösungsmenge der Gleichung $f'\,(x)=0$ wird berechnet. Alle Lösungen dieser Gleichung sind mögliche sogenannte Extremstellen.

Die Bedingung $f'\,(x)=0$ ist allerdings nur eine notwendige Bedingung für Extremstellen. Eine Stelle mit der Steigung 0 könnte auch ein Sattelpunkt sein. Das Standardbeispiel ist $f(x)=x^{3}$ an der Stelle 0. Obwohl $f'\,(0)=0$ gilt, ist der Punkt $(0|0)$ kein Extrempunkt, sondern ein Sattelpunkt.

Zum Nachweis der Extrempunkteigenschaft benötigt man daher eine der weiter unten genannten hinreichenden Bedingungen.

Notwendige Bedingung

Es leuchtet anschaulich ein, dass die Tangente an einen Funktionsgraphen in einem Extrempunkt parallel zur $x$-Achse verlaufen muss. Die Steigung einer solchen Tangente muss also den Wert 0 haben. Präziser gilt:

• $f$ sei eine reelle Funktion, die auf einem offenen Intervall $I$ definiert und an der Stelle $x_{0}$ (mit $x_{0}\in I$) differenzierbar ist. Nimmt $f$ an der Stelle $x_{0}$ ein relatives Extremum (also ein relatives Maximum oder Minimum) an, so gilt $f'\,(x_{0})=0$.

Am Rand des Definitionsbereichs und an Stellen, an denen die gegebene Funktion nicht differenzierbar ist, sind die Voraussetzungen dieser Bedingung nicht erfüllt. Relative Extrema an solchen Stellen lassen sich also im Allgemeinen nicht durch Nullsetzen der Ableitung bestimmen.

Hinreichende Bedingung: Wert der zweiten Ableitung

Die folgende hinreichende Bedingung bietet oft eine bequeme Möglichkeit, den Nachweis für ein relatives Extremum zu führen und zugleich die Art (Maximum oder Minimum) zu bestimmen. Da auch die zweite Ableitung benötigt wird, spricht man gelegentlich vom $f''$-Test.

• $f$ sei eine reelle Funktion, die in einem offenen Intervall $I$ definiert und zweimal differenzierbar ist.

Gilt an einer Stelle $x_{0}\in I$ zugleich

1. $f'(x_{0})=0$ und
2. $f''(x_{0})>0$,

so hat $f$ an dieser Stelle ein relatives Minimum.

Gilt dagegen zugleich

1. $f'(x_{0})=0$ und
2. $f''(x_{0})<0$,

so hat $f$ an dieser Stelle ein relatives Maximum.

Beispiel:

${\begin{aligned}f(x)&=-x^{2}+8x\\f'(x)&=-2x+8\\f''(x)&=-2\end{aligned}}$

Durch Nullsetzen der ersten Ableitung ($-2x+8=0$) erhält man $x=4$. Einsetzen in die zweite Ableitung ergibt $f''(4)=-2<0$ (Bedingung für ein relatives Maximum). Der Graph von $f$ hat also genau einen Extrempunkt, nämlich einen Hochpunkt mit der $x$-Koordinate 4.

Gelegentlich gilt sowohl $f'(x_{0})=0$ als auch $f''(x_{0})=0$. In diesem Fall sind weitere Untersuchungen nötig, um zu entscheiden, ob eine Extremstelle vorliegt oder nicht. Das bedeutet konkret, dass solange abgeleitet werden muss, bis eine Ableitung gerader Ordnung – vierter, sechster, … Ordnung – vorliegt, die an dieser Stelle ungleich 0 ist.

Das einfachste Beispiel ist $f(x)=x^{4}$. Die ersten drei Ableitungen an der Stelle $x_{0}=0$, also $f'(0)$, $f''(0)$ und $f'''(0)$ haben jeweils den Wert 0. Erst die vierte Ableitung $f^{(4)}(x)=24$ ermöglicht wegen $f^{(4)}(0)=24\neq 0$ den Nachweis des Extremums. Das positive Vorzeichen lässt erkennen, dass sich an der Stelle $x_{0}=0$ ein relatives Minimum befindet.

In seltenen Fällen versagt auch dieses allgemeinere Kriterium, nämlich dann, wenn alle Ableitungen an der Stelle $x_{0}$ gleich 0 sind.

Hinreichende Bedingung: Vorzeichen der ersten Ableitung

Ein weiteres Verfahren zum Nachweis der Extrempunkteigenschaft kommt ohne die Berechnung der zweiten Ableitung aus. Es wird untersucht, ob die erste Ableitung $f'(x)$ an der betrachteten Stelle $x_{0}$ ihr Vorzeichen wechselt. Diese Methode, gelegentlich als Vorzeichenwechsel-Verfahren (VZW-Verfahren) bezeichnet, lässt sich folgendermaßen anschaulich deuten:

Durchläuft man den Funktionsgraphen in der Umgebung eines Hochpunkts von links nach rechts, so lässt sich das Aussehen dieser Kurve wie folgt beschreiben:

1. Links vom Hochpunkt steigt der Funktionsgraph an. Die Steigung ist positiv.
2. Im Hochpunkt selbst verläuft die Tangente waagerecht. Die Steigung ist 0.
3. Rechts vom Hochpunkt fällt der Funktionsgraph. Die Steigung ist negativ.

Entsprechendes, nur umgekehrt, gilt für Tiefpunkte.

• $f$ sei eine reelle Funktion, die in einem offenen Intervall $I$ definiert und differenzierbar ist.

Gilt an einer Stelle $x_{0}\in I$ zugleich

1. $f'(x_{0})=0$,
2. $f'(x)<0$ für $x<x_{0},\,x\in I$ und
3. $f'(x)>0$ für $x>x_{0},\,x\in I$,

so hat $f$ an dieser Stelle ein relatives Minimum.

Gilt an einer Stelle $x_{0}\in I$ zugleich

1. $f'(x_{0})=0$,
2. $f'(x)>0$ für $x<x_{0},\,x\in I$ und
3. $f'(x)<0$ für $x>x_{0},\,x\in I$,

so hat $f$ an dieser Stelle ein relatives Maximum.

Beispiel:

$f(x)=x^{4}$

$f'(x)=4x^{3}$

Nullsetzen der Ableitung ($4x^{3}=0$) liefert als Stelle mit waagerechter Tangente und damit als Kandidaten für eine Extremstelle $x=0$. Beim VZW-Test betrachtet man $x$-Werte, die kleiner bzw. größer als 0 sind.

$f'(x)=4x^{3}<0$ für $x<0$

$f'(x)=4x^{3}>0$ für $x>0$

zeigt, dass ein Tiefpunkt vorliegt.

Ein Problem des VZW-Tests besteht darin, dass das Vorzeichen der Ableitung nicht nur für eine einzige Stelle ermittelt werden muss, sondern für ein ganzes Intervall. In der Schulmathematik bestimmt man daher oft nur für eine einzelne Stelle des Intervalls das Vorzeichen und schließt daraus, dass dieses Vorzeichen im ganzen Intervall gilt. Diese Vorgehensweise ist erlaubt, wenn die Funktion im Intervall $I$ stetig differenzierbar ist.

Historische Randbemerkung: Die Bestimmung der Extrema aus der Tangentensteigung wurde erstmals von Fermat in einem Brief an Descartes vorgeschlagen – bevor es den Ableitungsbegriff gab.

Wendepunkte

→ Hauptartikel: Wendepunkt

Als Wendepunkte bezeichnet man diejenigen Punkte, in denen der gegebene Funktionsgraph zwischen Links- und Rechtskrümmung wechselt. Die Art der Krümmung lässt sich – unter gewissen Voraussetzungen – am Vorzeichen der zweiten Ableitung $f''(x)$ erkennen. Positives Vorzeichen lässt auf Linkskrümmung schließen, negatives Vorzeichen auf Rechtskrümmung. Beim Standardverfahren zur Bestimmung der Wendepunkte setzt man daher die zweite Ableitung gleich 0. Die Lösungen der Gleichung $f''(x)=0$ (siehe notwendige Bedingung) kommen als Wendestellen in Frage. Mit einer der unten aufgeführten hinreichenden Bedingungen weist man anschließend nach, dass tatsächlich ein Wendepunkt vorliegt.

An bayerischen Beruflichen Oberschulen werden Wendestellen als Extremstellen der ersten Ableitung definiert.

Notwendige Bedingung

• $f$ sei eine reelle Funktion, die in einem offenen Intervall $I$ definiert und zweimal stetig differenzierbar ist. Hat der Graph von $f$ an der Stelle $x_{0}\in I$ einen Wendepunkt, so gilt

$f''(x_{0})=0.$

Hinreichende Bedingung: Wert der dritten Ableitung

Die zuletzt genannte Bedingung ist nicht hinreichend, sodass weitere Untersuchungen durchzuführen sind. Eine häufig zum Nachweis von Wendepunkten verwendete hinreichende Bedingung beruht auf der dritten Ableitung:

• $f$ sei eine reelle Funktion, die in einem offenen Intervall $I$ definiert und dreimal differenzierbar ist. Gilt an einer Stelle $x_{0}\in I$ zugleich

1. $f''(x_{0})=0$ und
2. $f'''(x_{0})\neq 0,$

so hat der Graph von $f$ an der Stelle $x_{0}$ eine Wendestelle.

Hinreichende Bedingung: Vorzeichen der zweiten Ableitung

Ist an der Stelle $x_{0}$ neben der zweiten Ableitung auch die dritte Ableitung gleich 0, so versagt das zuletzt genannte Kriterium. In diesem Fall untersucht man, ob die zweite Ableitung bei $x_{0}$ das Vorzeichen wechselt. Zu diesem Zweck wählt man sich einen Wert kleiner und einen größer als die Nullstelle der zweiten Ableitung (also der $x$-Koordinate des Wendepunktes). Diese beiden Werte werden in die zweite Ableitung eingesetzt. Unterscheiden sich die Vorzeichen der Werte der zweiten Ableitung an diesen Stellen, so liegt ein Wendepunkt vor. Wechselt das Vorzeichen von Minus nach Plus, so handelt es sich um eine Wendestelle mit einem Übergang von einer Rechts- in eine Linkskrümmung. Wechselt das Vorzeichen von Plus nach Minus, so handelt es sich um eine Wendestelle mit einem Übergang von einer Links- in eine Rechtskrümmung.

• $f$ sei eine reelle Funktion, die im offenen Intervall $I$ definiert und zweimal differenzierbar ist. Gilt an der Stelle $x_{0}\in I$ zugleich

1. $f''(x_{0})=0$,
2. $f''(x)<0$ für $x<x_{0}$, $x\in I$ und
3. $f''(x)>0$ für $x>x_{0}$, $x\in I$

oder zugleich

1. $f''(x_{0})=0$,
2. $f''(x)>0$ für $x<x_{0}$, $x\in I$ und
3. $f''(x)<0$ für $x>x_{0}$, $x\in I$,

so hat der Graph von $f$ an der Stelle $x_{0}$ eine Wendestelle.

Spezialfall: Sattelpunkte

Einen Wendepunkt mit zugleich waagerechter Tangente nennt man einen Sattelpunkt oder Terrassenpunkt. Für ihn gilt demnach $f'(x)=0$ und $f''(x)=0$, wie im Beispiel der Funktion mit der Gleichung

$f(x)={x^{3}}$

an der Stelle $x=0$.

Allerdings ist das kein hinreichendes Kriterium, es kann auch $f'(x)=0$ und $f''(x)=0$ werden, ohne dass ein Sattelpunkt auftritt, wie im nachfolgenden Beispiel gezeigt wird:

$f(x)={x^{4}}$

Erst wenn $f'''\neq 0$ ist, ist ein Sattelpunkt erwiesen; allgemeiner gilt: Es liegt ein Wendepunkt vor, wenn der Grad der ersten von 0 verschiedenen Ableitung ungerade ist; ist der Grad gerade, so handelt es sich um ein Extremum. In Fällen wie

$f(x)={x^{5}}$

ist allerdings die dritte Ableitung unnütz, da auch diese an der Stelle 0 verschwindet. Hier hilft das Vorzeichenwechselkriterium weiter.

Polstellen

Eine Polstelle liegt bei gebrochen-rationalen Funktionen genau dann an einer Stelle $p$ vor, wenn das Nennerpolynom eine Nullstelle bei $p$ hat und das Zählerpolynom eine Nullstelle einer niedrigeren Ordnung bei $p$ oder keine Nullstelle bei $p$ hat.

Haben sowohl das Zähler- als auch das Nennerpolynom bei $p$ eine Nullstelle und ist die Ordnung der Nullstelle im Zählerpolynom nicht kleiner als die des Nennerpolynoms, handelt es sich um eine stetig behebbare Definitionslücke.

In der Hochschulmathematik gibt es noch weitere Arten von nicht definierten Stellen, die weder hebbare Lücken noch Polstellen sind.

Lücke

Im Falle von gebrochenrationalen Funktionen liegt an einer Stelle $x_{0}$ eine stetig behebbare Definitionslücke vor, falls $x_{0}$ nicht nur eine Nullstelle des Nenners, sondern auch eine Nullstelle des Zählers von mindestens gleich großem Grad ist. In diesem Fall lässt sich der zugehörige Linearfaktor $(x-x_{0})$ herauskürzen.

Beispiel: ${\tfrac {x^{2}-4}{x-2}}$ hat an der Stelle $x=2$ eine behebbare Definitionslücke. Durch Kürzen des Faktors $(x-2)$ entsteht:

${\frac {x^{2}-4}{x-2}}={\frac {(x+2)\cdot (x-2)}{x-2}}=x+2$   (für $x\neq 2$).

Eine andere Möglichkeit zu testen, ob an der Stelle $x_{0}$ eine stetig behebbare Definitionslücke vorliegt, besteht darin, den Grenzwert $\lim _{x\rightarrow x_{0}}f(x)$ zu berechnen. Wenn dieser Limes existiert und endlich ist, liegt eine stetig behebbare Lücke vor.

Verhalten im Unendlichen

Um das Verhalten im Unendlichen herauszufinden, wird der Funktionswert der Funktion $f(x)$ untersucht, wenn $x$ über alle Grenzen wächst, also gegen $\infty$ geht:

$\lim _{x\to \infty }f(x)\;;$

Entsprechendes für $-\infty$.

Übersicht über Kriterien

Diskutiert wird $f\colon x\mapsto f(x)$
Untersuchungsaspekt	Kriterium
Nullstelle	$f(x_{N})=0\,$
Extremstelle	$f'(x_{E})=0\,$	(notwendiges Kriterium)
	$f'(x_{E})=0\land f''(x_{E})\neq 0$	(hinreichendes Kriterium)
Minimalstelle	$f'(x_{E})=0\,$	(notwendiges Kriterium)
	$f'(x_{E})=0\land f''(x_{E})>0$	(hinreichendes Kriterium)
Maximalstelle	$f'(x_{E})=0\,$	(notwendiges Kriterium)
	$f'(x_{E})=0\land f''(x_{E})<0$	(hinreichendes Kriterium)
Wendestelle	$f''(x_{W})=0\,$	(notwendiges Kriterium)
	$f''(x_{W})=0\land f'''(x_{W})\neq 0$	(hinreichendes Kriterium)
Sattelstelle	$f'(x_{W})=0\land f''(x_{W})=0$	(notwendiges Kriterium)
	$f'(x_{W})=0\land f''(x_{W})=0\land f'''(x_{W})\neq 0$	(hinreichendes Kriterium)
Verhalten im Unendlichen	$\lim _{x\to \infty }f(x)$,	$\lim _{x\to -\infty }f(x)$
Symmetrie
Achsensymmetrie zur Koordinatenachse	$f(x)=f(-x)\,$
Punktsymmetrie zum Koordinatenursprung	$-f(x)=f(-x)\,$
Monotonie
steigend/streng steigend	$f'(x)\geq 0$	$f'(x)>0\,$
fallend/streng fallend	$f'(x)\leq 0$	$\,f'(x)<0$
Krümmung
Linkskrümmung/Konvexbogen (nach oben offen)	$f''(x)>0\,$
Rechtskrümmung/Konkavbogen (nach unten offen)	$f''(x)<0\,$
Periodizität	$f(x+p)=f(x)\,$
Diskutiert wird $f\colon x\mapsto {\frac {p(x)}{q(x)}}$
Untersuchungsaspekt	Kriterium
Definitionsbereich	$\mathbb {D} =\mathbb {R} \setminus \lbrace x_{0}\mid q(x_{0})=0\rbrace$
Polstelle	$q(x_{p})=0\,$	(notwendiges Kriterium)
	$q(x_{p})=0\land p(x_{p})\neq 0$	(hinreichendes Kriterium)

Beispiel: Ganzrationale Funktion

Graphen der Funktionen f (schwarz), f ' (rot) und f '' (blau)

Die zu untersuchende Funktion sei:

$f(x)=3x^{3}-5x^{2}+8$

Der Graph der Funktion $f$ ist im Bild schwarz dargestellt, zudem sind die erste (rot) und zweite (blau) Ableitung eingetragen:

Nullstellen

Durch Ausprobieren (zum Beispiel durch Anfertigen einer Wertetabelle) oder gemäß der Folgerung mit dem Wissen nach Gauß, dass jede ganzzahlige Nullstelle Teiler des absoluten Gliedes 8 sein muss, lässt sich die Nullstelle $x=-1$ finden. Gäbe es keine derart einfach erkennbare Nullstelle, so ließe sich die Formel von Cardano für Gleichungen 3. Grades oder das newtonsche Näherungsverfahren anwenden.

Zur Nullstelle $x=-1$ gehört der Linearfaktor $(x-(-1))=(x+1)$. Um die weiteren Nullstellen zu finden, wird eine Polynomdivision durch diesen Linearfaktor durchgeführt und das Ergebnis gleich 0 gesetzt. Etwas schneller erhält man das Ergebnis mit dem Horner-Schema. Auf diese Weise reduziert sich der Grad der Gleichung um 1.

$(3x^{3}-5x^{2}+8):(x+1)=3x^{2}-8x+8$

Die neue Gleichung $3x^{2}-8x+8=0$ hat keine Lösung. $x=-1$ ist folglich die einzige reelle Nullstelle.

Extrempunkte

Die erste Ableitungsfunktion ist

$f'(x)=9x^{2}-10x=9x(x-{\tfrac {10}{9}})\,$.

Diese besitzt Nullstellen bei $x_{1}=0$ und bei $x_{2}={\tfrac {10}{9}}$. Dies bedeutet, dass hier Extremstellen vorliegen können.

Die zweite Ableitungsfunktion

$f''(x)=18x-10\,$

hat an obigen Stellen die Funktionswerte

$f''(x_{1})=18\cdot 0-10=-10<0$

bzw.

$f''(x_{2})=18\cdot {\tfrac {10}{9}}-10=10>0.$

Daher hat der Funktionsgraph bei $x_{1}$ einen Hochpunkt (erste Ableitung gleich 0, zweite Ableitung negativ) und bei $x_{2}$ einen Tiefpunkt (erste Ableitung gleich 0, zweite Ableitung positiv). Die $y$-Koordinaten der beiden Extrempunkte ergeben sich durch Einsetzen der $x$-Koordinaten in $f(x)$.

${\begin{aligned}y_{1}&=f(0)=3\cdot 0^{3}-5\cdot 0^{2}+8=8\\y_{2}&=f({\tfrac {10}{9}})=3\cdot \left({\tfrac {10}{9}}\right)^{3}-5\cdot \left({\tfrac {10}{9}}\right)^{2}+8=5{\tfrac {229}{243}}\end{aligned}}$

Hochpunkt: $(0|8)$

Tiefpunkt: $({\tfrac {10}{9}}|5{\tfrac {229}{243}})$

Wendepunkte

Zur Bestimmung der Wendestellen wird die zweite Ableitung $f''(x)=18x-10$ gleich null gesetzt:

$18x-10=0$

Die einzige Lösung dieser Gleichung ist $x_{3}={\tfrac {5}{9}}$. Zur Bestätigung, dass tatsächlich ein Wendepunkt vorliegt, kann man die dritte Ableitung $f'''(x)=18$ verwenden. Wegen

$f'''(x_{3})=f'''({\tfrac {5}{9}})=18\neq 0$

ist die Wendepunkteigenschaft gesichert. Die $y$-Koordinate des Wendepunkts ergibt sich zu

$y_{3}=f(x_{3})=3\cdot \left({\tfrac {5}{9}}\right)^{3}-5\cdot \left({\tfrac {5}{9}}\right)^{2}+8=6{\tfrac {236}{243}}.$

Wendepunkt: $({\tfrac {5}{9}}|6{\tfrac {236}{243}})$

Polstellen und Verhalten im Unendlichen

Polstellen gibt es bei Polynomen nicht. Als Polynom ungeradzahliger Ordnung (höchster Exponent bei $x^{3}$) geht die Funktion gegen $+\infty$ bzw. $-\infty$, wenn $x$ gegen $+\infty$ bzw. $-\infty$ geht.

Beispiel: Gebrochen-rationale Funktion

Graphen der Funktionen f (rot), f ' (blau) und f '' (grün)

Gegeben ist die Funktion mit der Gleichung

${f(x)}={\frac {x^{3}-4x^{2}+4x}{4x^{2}-8x+4}}$

Definitionsbereich

Die Funktion ist nur dort definiert, wo der Nenner ungleich 0 ist. Die Untersuchung des Nenners auf Nullstellen ergibt:

$4x^{2}-8x+4=0$

$x^{2}-2x+1=0$

$x=1+{\sqrt {1-1}}=1$ oder $x=1-{\sqrt {1-1}}=1$

Die quadratische Gleichung hat eine doppelte Lösung bei $x=1$. Nur bei $x=1$ wird also der Nenner 0. Der Definitionsbereich ist folglich

$\mathbb {D} =\mathbb {R} \setminus \{1\},$

die Menge der reellen Zahlen, ausgenommen die 1. Der Nenner kann – in Linearfaktoren zerlegt – als

$4(x-1)(x-1)$ oder $4(x-1)^{2}$

geschrieben werden.

Nullstellen

Die Bedingung für Nullstellen ist $f(x_{N})=0\,$. Hierzu genügt es, dass der Zähler 0 wird, solange nicht zugleich der Nenner 0 wird. Untersuchung des Zählers auf Nullstellen ergibt:

$x^{3}-4x^{2}+4x=0$

$x(x^{2}-4x+4)=0$

$x=0$ oder $x=2+{\sqrt {4-4}}=2$ oder $x=2-{\sqrt {4-4}}=2$

Der Zähler hat eine einfache Nullstelle bei $x=0$ und eine doppelte bei $x=2$. Beide Stellen liegen im Definitionsbereich. $f(x)$ hat also die Nullstellen $x_{1}=0$ sowie $x_{2}=x_{3}=2$.

Der Zähler kann – in Linearfaktoren zerlegt – als

$x(x-2)(x-2)=x(x-2)^{2}$

geschrieben werden.

Im Rahmen der Schulmathematik wird häufig darauf Wert gelegt, dass bei jedem $x$ der Index $N$ für „Nullstelle“ dazugeschrieben wird: $x_{N}\,$.

Polstellen

An der Stelle $x=1$ hat der Nenner eine zweifache Nullstelle, ohne dass zugleich der Zähler 0 wird. Es liegt also eine Polstelle bei $x=1$ vor. Sollte der Zähler auch 0 werden, so muss für eine Polstelle die Ordnung der Nennernullstelle größer als die Ordnung der Zählernullstelle sein.

Sofern der Nenner einer gebrochenrationalen Funktion an einer Stelle $x=a$ gleich 0 ist, ist die Funktion an dieser Stelle nicht definiert. Ist der Nenner gleich 0, der Zähler aber ungleich 0, so besitzt die Funktion an dieser Stelle einen Pol („Unendlichkeitsstelle“).

Symmetrie

Der Graph der Funktion wird an dieser Stelle auf Symmetrie untersucht. Oft erfolgt nur eine Untersuchung auf Achsensymmetrie zur $y$-Achse (Bedingung $f(-x)=f(x)$) und auf Punktsymmetrie zum Ursprung des Koordinatensystems (Bedingung $f(-x)=-f(x)$).

Im Beispiel wird in

${f(x)}={{x^{3}-4x^{2}+4x} \over {4x^{2}-8x+4}}$

$x$ ersetzt durch $-x$. Nach dem Ausmultiplizieren entsteht

${f(-x)}={{(-x)^{3}-4(-x)^{2}+4(-x)} \over {4(-x)^{2}-8(-x)+4}}={{-x^{3}-4x^{2}-4x} \over {4x^{2}+8x+4}}$.

Da $f(-x)$ weder mit $f(x)$ noch mit $-f(x)$ übereinstimmt, ist der Graph von $f$ weder achsensymmetrisch zur $y$-Achse noch punktsymmetrisch zum Ursprung.

Etwas schwieriger gestaltet sich die Untersuchung auf Achsensymmetrie bezüglich einer beliebigen Achse beziehungsweise auf Punktsymmetrie bezüglich eines beliebigen Punktes. Wegen $\textstyle \lim _{x\to -\infty }f(x)=-\infty$ und $\textstyle \lim _{x\to \infty }f(x)=+\infty$ lässt sich Achsensymmetrie ausschließen. Als Symmetriezentrum (Punktsymmetrie) käme höchstens der Schnittpunkt der Asymptoten (siehe unten), also der Punkt $(1|-{\tfrac {1}{4}})$ in Frage. Da aber beispielsweise die Punkte $(0|0)$ und $(2|0)$ nicht symmetrisch bezüglich $(1|-{\tfrac {1}{4}})$ liegen, ist der Graph auch nicht punktsymmetrisch.

Ableitungen

Zu bilden sind die Ableitungen von

${f(x)}={{x(x-2)^{2}} \over {4(x-1)^{2}}}.$

Die Darstellung in Linearfaktoren ist zweckmäßiger, da sie das Ausklammern und Kürzen vereinfacht. Dies ergibt zunächst

${\begin{aligned}{f'(x)}&={{(2x(x-2)+(x-2)^{2})4(x-1)^{2}-x(x-2)^{2}\cdot 8(x-1)} \over {16(x-1)^{4}}}\\&={{(2x(x-2)+(x-2)^{2})(x-1)-2x(x-2)^{2}} \over {4(x-1)^{3}}}\\&={{(x-2)((2x+(x-2))(x-1)-2x(x-2))} \over {4(x-1)^{3}}}\\&={{(x-2)((3x-2)(x-1)-2x(x-2))} \over {4(x-1)^{3}}}\\&={{(x-2)(3x^{2}-3x-2x+2-2x^{2}+4x)} \over {4(x-1)^{3}}}\\&={{(x-2)(x^{2}-x+2)} \over {4(x-1)^{3}}}\end{aligned}}$

für die erste Ableitung. Dann wird die zweite

${\begin{aligned}{f''(x)}&={{((x-2)(2x-1)+(x^{2}-x+2))(x-1)^{3}-(x-2)(x^{2}-x+2)\cdot 3(x-1)^{2}} \over {4(x-1)^{6}}}\\&={{((x-2)(2x-1)+(x^{2}-x+2))(x-1)-3(x-2)(x^{2}-x+2)} \over {4(x-1)^{4}}}\\&={{(2x^{2}-x-4x+2+x^{2}-x+2)(x-1)-(3x-6)(x^{2}-x+2)} \over {4(x-1)^{4}}}\\&={{(3x^{2}-6x+4)(x-1)-(3x^{3}-3x^{2}+6x-6x^{2}+6x-12)} \over {4(x-1)^{4}}}\\&={{3x^{3}-3x^{2}-6x^{2}+6x+4x-4-3x^{3}+3x^{2}-6x+6x^{2}-6x+12} \over {4(x-1)^{4}}}\\&={{-2x+8} \over {4(x-1)^{4}}}\\&={{4-x} \over {2(x-1)^{4}}}\end{aligned}}$

und die dritte Ableitung

${\begin{aligned}{f'''(x)}&={-{(x-1)^{4}-(4-x)4(x-1)^{3}} \over {2(x-1)^{8}}}\\&={-{(x-1)-4(4-x)} \over {2(x-1)^{5}}}\\&={-{x+1-16+4x} \over {2(x-1)^{5}}}\\&={{3x-15} \over {2(x-1)^{5}}}\end{aligned}}$

gebildet.

Extrempunkte

Hierfür muss $f'(x)=0\,$ werden. Es genügt, die Nullstellen des Zählers zu untersuchen:

${(x-2)(x^{2}-x+2)}=0\,$

hat die Lösung $x=2$. Die zweite Klammer hat keine reellen Lösungen. $x=2$ liegt im Definitionsbereich. Der Funktionswert an dieser Stelle ist $f(2)=0\,$, da hier eine Nullstelle vorliegt. Die zweite Ableitung ist an dieser Stelle $f''(2)=1>0\,$, es handelt sich also um einen Tiefpunkt bei (2/ 0).

Wendepunkte

Der Wendepunkt wird ermittelt, indem die zweite Ableitung gleich 0 gesetzt wird. Aus diesem Ansatz ergibt sich $x_{W}=4$. Einsetzen dieses Wertes in die dritte Ableitung ergibt $f'''(4)=-{\tfrac {1}{162}}\neq 0$. Es liegt also tatsächlich ein Wendepunkt vor. Die Berechnung von $f(4)$ ergibt schließlich die $y$-Koordinate $y_{W}={\tfrac {4}{9}}$. Der gesuchte Wendepunkt ist somit $(4|{\tfrac {4}{9}})$.

Asymptoten

An der Polstelle, also bei $x=1$, liegt eine senkrechte Asymptote. Da der Grad des Zählers (3) um 1 größer ist als der des Nenners (2), wird $f(x)$ gegen $\infty$ gehen für $x$ gegen $\infty$. Die Differenz $3-2=1$ gibt an, dass sich der Graph an eine lineare Funktion (Gerade) asymptotisch annähern wird. Die Geradengleichung folgt durch Polynomdivision:

$(x^{3}-4x^{2}+4x):(4x^{2}-8x+4)={{1 \over 4}x-{1 \over 2}+{{-1x+2} \over {4x^{2}-8x+4}}}$

Für $x$ gegen $\infty$ geht der letzte Term gegen 0. Die Gleichung der Asymptote ist also

${a(x)}={{1 \over 4}x-{1 \over 2}}$

Allgemein:

• Ist der Nennergrad größer als der Zählergrad, ist die Asymptote die $x$-Achse.
• Ist der Nennergrad gleich dem Zählergrad, ist die Asymptote eine Parallele zur $x$-Achse.
• Ist der Nennergrad um 1 kleiner als der Zählergrad, ist die Asymptote schräg.
• Ist der Nennergrad um mehr als 1 kleiner als der Zählergrad, ist die Asymptote keine Gerade, sondern gekrümmt. (Asymptotische Näherungskurve)

Didaktische Fragen

In der Mathematikdidaktik wird seit spätestens den 1990er Jahren diskutiert, inwieweit die Kurvendiskussion durch die Verfügbarkeit von grafikfähigen Taschenrechnern und dedizierter Software (Funktionenplotter) überholt ist.

Kritisiert wird, dass die Kurvendiskussion eine rein rechnerische Routine ist, die wenig Verständnis vermittelt. Andererseits ist sie gerade deshalb als relativ sicher vorzubereitendes Prüfungsthema bei schwächeren Schülern und Studenten vergleichsweise beliebt.

In den zentralen Abiturprüfungen hat es sich deshalb durchgesetzt, dass solch schematische Aufgaben nur sehr selten gestellt werden. Beliebter sind eingekleidete Aufgaben oder Aufgaben, in denen Zusammenhangswissen abgefragt wird, zum Beispiel über Zusammenhänge zwischen Ableitungsfunktion und Ausgangsfunktion.

Eine didaktische Methode wird in Gebietseinteilung beschrieben.

Literatur

• Harald Scheid, Wolfgang Schwarz: Elemente der Linearen Algebra und der Analysis. Springer, 2009, ISBN 978-3-8274-2255-2, S. 316–322.
• Harro Heuser: Lehrbuch der Analysis. Teil 1. Vieweg + Teubner, Wiesbaden 1980, ISBN 3-519-02221-4, S. 293–295.
• Kurvendiskussion In: Schülerduden – Mathematik II. Bibliographisches Institut & F.A. Brockhaus, 2004, ISBN 3-411-04275-3, S. 235–241.
• Mathematik – Analysis. Cornelsen, 2002, ISBN 978-3-464-57216-0, S. 108–142.

Weblinks

• Verständlicher Text zur Kurvendiskussion
• Exemplarische Kurvendiskussionen
• Online Rechner zur Kurvendiskussion mit Rechenweg