Binomialverteilung

Binomialverteilung
Wahrscheinlichkeitsfunktion 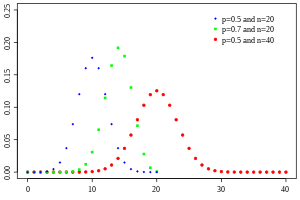Drei Wahrscheinlichkeitsfunktionen für Binomialverteilungen mit den Parametern $(n;p)=(20;0{,}5)$, $(n;p)=(20;0{,}7)$ und $(n;p)=(40;0{,}5)$
Verteilungsfunktion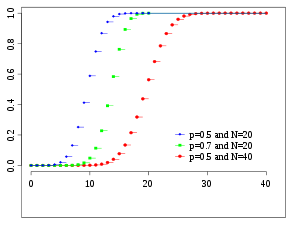 Drei Verteilungsfunktionen für Binomialverteilungen mit den Parametern $(n;p)=(20;0{,}5)$, $(n;p)=(20;0{,}7)$ und $(n;p)=(40;0{,}5)$
Parameter	$n\in \mathbb {N} ^{+}$, $p\in [0,1]$
Träger	$k\in \{0,\dotsc ,n\}$
Wahrscheinlichkeitsfunktion	$\textstyle {n \choose k}\,p^{k}(1-p)^{n-k}$
Verteilungsfunktion	$I_{1-p}(n-\lfloor k\rfloor ,1+\lfloor k\rfloor )$
Erwartungswert	$np$
Median	i. A. keine geschlossene Formel, siehe unten
Modus	$\lfloor (n+1)p\rfloor$ oder $\lfloor (n+1)p-1\rfloor$
Varianz	$np(1-p)$
Schiefe	${\frac {1-2p}{\sqrt {np(1-p)}}}\quad (0<p<1)$
Wölbung	$3+{\frac {1-6p(1-p)}{np(1-p)}}\quad (0<p<1)$
Entropie	${\frac {1}{2}}\log _{2}{\big (}2\pi \mathrm {e} \,np(1-p){\big )}$ $+\operatorname {\mathcal {O}} \left({\frac {1}{n}}\right)\quad (0<p<1)$
Momenterzeugende Funktion	$\left(1-p+p\mathrm {e} ^{t}\right)^{n}$
Charakteristische Funktion	$\left(1-p+p\mathrm {e} ^{\mathrm {i} t}\right)^{n}$

Die Binomialverteilung ist eine der wichtigsten diskreten Wahrscheinlichkeitsverteilungen.

Wahrscheinlichkeitsfunktion der Binomialverteilung für $n=20$; $p=0{,}1$ (blau), $p=0{,}5$ (grün) und $p=0{,}8$ (rot)

Binomialverteilungen für $p=0{,}5$
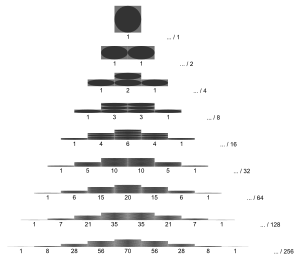
mit $n$ und $k$ wie im Pascalschen Dreieck

Die Wahrscheinlichkeit, dass eine Kugel in einem Galtonbrett mit acht Ebenen ($n=8$) ins mittlere Fach fällt ($k=4$), ist $70/256$.

Sie beschreibt die Anzahl der Erfolge in einer Serie von gleichartigen und unabhängigen Versuchen, die jeweils genau zwei mögliche Ergebnisse haben („Erfolg“ oder „Misserfolg“). Solche Versuchsserien werden auch Bernoulli-Prozesse genannt.

Ist $p$ die Erfolgswahrscheinlichkeit bei einem Versuch und $n$ die Anzahl der Versuche, dann bezeichnet man mit $B(k\mid p,n)$ (auch $B_{n,p}(k)$, $B(n,p,k)$ oder $B(n;p;k)$) die Wahrscheinlichkeit, genau $k$ Erfolge zu erzielen (siehe Abschnitt Definition).

Die Binomialverteilung und der Bernoulli-Versuch können mit Hilfe des Galtonbretts veranschaulicht werden. Dabei handelt es sich um eine mechanische Apparatur, in die man Kugeln wirft. Diese fallen dann zufällig in eines von mehreren Fächern, wobei die Aufteilung der Binomialverteilung entspricht. Je nach Konstruktion sind unterschiedliche Parameter $n$ und $p$ möglich.

Obwohl die Binomialverteilung bereits lange vorher bekannt war, wurde der Begriff zum ersten Mal 1911 in einem Buch von George Udny Yule verwendet.

Definition

Wahrscheinlichkeitsfunktion, Verteilungsfunktion, Eigenschaften

Die diskrete Wahrscheinlichkeitsverteilung mit der Wahrscheinlichkeitsfunktion

$B(k\mid p,n)={\begin{cases}{\binom {n}{k}}p^{k}(1-p)^{n-k}&{\text{falls}}\quad k\in \left\{0,1,\dots ,n\right\},\\0&{\text{sonst.}}\end{cases}}$

heißt die Binomialverteilung zu den Parametern $n\in \mathbb {N}$ (Anzahl der Versuche) und $p\in \left[0,1\right]$ (der Erfolgs- oder Trefferwahrscheinlichkeit). Bei dieser Formel wird die Konvention $0^{0}:=1$ angewendet (siehe dazu null hoch null).

Eine Zufallsvariable, deren Wahrscheinlichkeitsverteilung eine Binomialverteilung ist, heißt binomialverteilt. Die Binomialverteilung mit den Parametern $n$ und $p$ wird mit ${\mathcal {B}}(n,p)$ oder $\mathrm {Bin} (n,p)$ bezeichnet. Wenn eine Zufallsvariable $X$ die Binomialverteilung $\mathrm {Bin} (n,p)$ besitzt, so wird dies $X\sim \mathrm {Bin} (n,p)$ notiert.

Die obige Formel kann so verstanden werden: Wir brauchen bei insgesamt $n$ Versuchen genau $k$ Erfolge der Wahrscheinlichkeit $p^{k}$ und haben demzufolge genau $n-k$ Fehlschläge der Wahrscheinlichkeit $(1-p)^{n-k}$. Allerdings kann jeder der $k$ Erfolge bei jedem der $n$ Versuche auftreten, sodass wir noch mit der Anzahl ${\tbinom {n}{k}}$ der $k$-elementigen Teilmengen einer $n$-elementigen Menge multiplizieren müssen. Denn genau so viele Möglichkeiten gibt es, aus allen $n$ Versuchen die $k$ erfolgreichen auszuwählen.

Die zur Erfolgswahrscheinlichkeit $p$ komplementäre Ausfallwahrscheinlichkeit $1-p$ wird häufig mit $q$ abgekürzt.

Wie für eine Wahrscheinlichkeitsverteilung notwendig, müssen sich die Wahrscheinlichkeiten für alle möglichen Werte $k$ zu 1 summieren. Dies ergibt sich aus dem binomischen Lehrsatz wie folgt:

$\sum _{k=0}^{n}{\binom {n}{k}}p^{k}(1-p)^{n-k}=\left(p+\left(1-p\right)\right)^{n}=1^{n}=1$

Eine mit der Wahrscheinlichkeitsfunktion $B(\cdot \mid p,n)$ verteilte Zufallsgröße $X$ heißt dementsprechend binomialverteilt mit den Parametern $n$ und $p$ sowie der Verteilungsfunktion

$F_{X}(x)=\operatorname {P} (X\leq x)=\sum _{k=0}^{\lfloor x\rfloor }{\binom {n}{k}}p^{k}(1-p)^{n-k}$,

wobei $\lfloor x\rfloor$ die Abrundungsfunktion bezeichnet.

Weitere gebräuchliche Schreibweisen der kumulierten Binomialverteilung sind $F(k\mid p,n)$, $F(n,p,k)$ und $F(n;p;k)$.

Herleitung als Laplace-Wahrscheinlichkeit

Versuchsschema: Eine Urne enthält $N$ Bälle, davon sind $M$ schwarz und $N-M$ weiß. Die Wahrscheinlichkeit $p$, einen schwarzen Ball zu ziehen, ist also $p={\frac {M}{N}}$. Es werden nacheinander zufällig $n$ Bälle entnommen, ihre Farbe bestimmt und wieder zurückgelegt.

Wir berechnen die Anzahl der Möglichkeiten, in denen man $k$ schwarze Bälle findet, und daraus die sogenannte Laplace-Wahrscheinlichkeit („Anzahl der für das Ereignis günstigen Möglichkeiten, geteilt durch die Gesamtanzahl der (gleichwahrscheinlichen) Möglichkeiten“).

Bei jeder der $n$ Ziehungen gibt es $N$ Möglichkeiten, insgesamt also $N^{n}$ Möglichkeiten für die Auswahl der Bälle. Damit genau $k$ dieser $n$ Bälle schwarz sind, müssen genau $k$ der $n$ Ziehungen einen schwarzen Ball aufweisen. Für jeden schwarzen Ball gibt es $M$ Möglichkeiten, und für jeden weißen Ball $N-M$ Möglichkeiten. Die $k$ schwarzen Bälle können noch auf ${\tbinom {n}{k}}$ mögliche Weisen über die $n$ Ziehungen verteilt sein, also gibt es

${\binom {n}{k}}M^{k}(N-M)^{n-k}$

Fälle, bei denen genau $k$ schwarze Bälle ausgewählt worden sind. Die Wahrscheinlichkeit $p_{k}$, unter $n$ Bällen genau $k$ schwarze zu finden, ist also

${\begin{aligned}p_{k}&={\binom {n}{k}}{\frac {M^{k}(N-M)^{n-k}}{N^{n}}}\\&={\binom {n}{k}}\left({\frac {M}{N}}\right)^{k}\left({\frac {N-M}{N}}\right)^{n-k}\\&={\binom {n}{k}}p^{k}(1-p)^{n-k}.\end{aligned}}$

Beispiele

Spielwürfel

Die Wahrscheinlichkeit, mit einem fairen Spielwürfel eine 6 zu würfeln, beträgt $p={\tfrac {1}{6}}$. Die Wahrscheinlichkeit $q$, dass dies nicht der Fall ist, beträgt $q=1-p={\tfrac {5}{6}}$. Angenommen, man würfelt 10-mal ($n=10$), dann beträgt die Wahrscheinlichkeit, dass kein einziges Mal eine 6 gewürfelt wird, $q^{10}=(1-p)^{10}=\left({\tfrac {5}{6}}\right)^{10}={\tfrac {9765625}{60466176}}\approx 0{,}162$. Die Wahrscheinlichkeit, dass genau 2-mal eine 6 gewürfelt wird, beträgt ${\binom {10}{2}}\left({\tfrac {1}{6}}\right)^{2}\left({\tfrac {5}{6}}\right)^{8}$. Allgemein wird die Wahrscheinlichkeit, dass man $k$-mal eine solche Zahl würfelt $(0\leq k\leq 10)$, durch die Binomialverteilung $B_{10,{\tfrac {1}{6}}}(k)$ beschrieben.

Häufig wird der durch die Binomialverteilung beschriebene Prozess auch durch ein sogenanntes Urnenmodell illustriert. In einer Urne seien z. B. 6 Kugeln, 1 davon weiß, die anderen schwarz. Man greife nun 10-mal in die Urne, hole eine Kugel heraus, notiere deren Farbe und lege die Kugel wieder zurück. In einer speziellen Deutung dieses Prozesses wird das Ziehen einer weißen Kugel als positives Ereignis mit der Wahrscheinlichkeit $p$ verstanden, das Ziehen einer nicht-weißen Kugel als negatives Ereignis. Die Wahrscheinlichkeiten sind genauso verteilt wie im Beispiel mit dem Spielwürfel.

Münzwurf

Eine Münze wird 7-mal geworfen. Wenn die diskrete Zufallsvariable $X$ die Anzahl der Würfe zählt, mit denen „Zahl“ geworfen wird, ergibt sich für $X$ eine Binomialverteilung mit der Wahrscheinlichkeitsfunktion

$P(X=k)=B(k\mid {\tfrac {1}{2}},7)={\begin{cases}{\binom {7}{k}}({\tfrac {1}{2}})^{k}(1-{\tfrac {1}{2}})^{7-k}&{\text{falls}}\quad k\in \left\{0,1,2,3,4,5,6,7\right\},\\0&{\text{sonst.}}\end{cases}}$

Die Werte und ihre Wahrscheinlichkeiten lassen sich in folgender Tabelle zusammenfassen:

$k$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$
$p_{k}=P(X=k)$	${\frac {1}{128}}$	${\frac {7}{128}}$	${\frac {21}{128}}$	${\frac {35}{128}}$	${\frac {35}{128}}$	${\frac {21}{128}}$	${\frac {7}{128}}$	${\frac {1}{128}}$

Der Erwartungswert der Zufallsvariablen $X$ ist

$\mathrm {E} [X]={\color {BrickRed}\mu }=np=7\cdot {\frac {1}{2}}={\color {BrickRed}3{,}5}$.

Die Varianz der Zufallsvariablen $X$ ist demnach gegeben durch

${\begin{aligned}\mathrm {Var[X]} =\sigma ^{2}&=\sum _{k=0}^{7}(k-{\color {BrickRed}\mu })^{2}p_{k}=(0-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {1}{128}}+(1-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {7}{128}}+(2-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {21}{128}}+(3-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {35}{128}}\\&\quad +(4-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {35}{128}}+(5-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {21}{128}}+(6-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {7}{128}}+(7-{\color {BrickRed}3{,}5})^{2}\cdot {\frac {1}{128}}={\frac {7}{4}}=1{,}75\end{aligned}}$

Mit dem Verschiebungssatz erhält man ebenfalls den gleichen Wert für die Varianz:

$\sigma ^{2}=\left(\sum _{k=0}^{7}k^{2}p_{k}\right)-{\color {BrickRed}\mu }^{2}=0^{2}\cdot {\frac {1}{128}}+1^{2}\cdot {\frac {7}{128}}+2^{2}\cdot {\frac {21}{128}}+3^{2}\cdot {\frac {35}{128}}+4^{2}\cdot {\frac {35}{128}}+5^{2}\cdot {\frac {21}{128}}+6^{2}\cdot {\frac {7}{128}}+7^{2}\cdot {\frac {1}{128}}-{\color {BrickRed}3{,}5}^{2}=1{,}75$.

Für die Standardabweichung ergibt sich damit:

$\sigma ={\sqrt {\sigma ^{2}}}={\sqrt {1{,}75}}\approx 1{,}323$.

Eigenschaften

Symmetrie

• Die Binomialverteilung ist in den Spezialfällen $p=0$, $p=0{,}5$ und $p=1$ symmetrisch und ansonsten asymmetrisch.
• Die Wahrscheinlichkeitsfunktion der Binomialverteilung besitzt die Eigenschaft

$B(k|p,n)=B(n-k|1-p,n)\quad {\text{für }}k\in \{0,1,\dots ,n\}$.

Erwartungswert

Eine binomialverteilte Zufallsvariable $X\sim B(n,p)$ besitzt den Erwartungswert $\operatorname {E} (X)=np$.

Beweis

Den Erwartungswert errechnet man direkt aus der Definition $\operatorname {E} (X)=\sum _{k=0}^{n}kP(X=k)$ und der Formel für die Einzelwahrscheinlichkeiten zu

${\begin{aligned}\operatorname {E} (X)&=\sum _{k=0}^{n}k{\binom {n}{k}}p^{k}(1-p)^{n-k}\\&=np\sum _{k=0}^{n}k{\frac {(n-1)!}{(n-k)!k!}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{k=1}^{n}{\frac {(n-1)!}{(n-k)!(k-1)!}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{k=1}^{n}{\binom {n-1}{k-1}}p^{k-1}(1-p)^{(n-1)-(k-1)}\\&=np\sum _{\ell =0}^{n-1}{\binom {n-1}{\ell }}p^{\ell }(1-p)^{(n-1)-\ell }\quad {\text{mit }}\ell :=k-1\\&=np\sum _{\ell =0}^{m}{\binom {m}{\ell }}p^{\ell }(1-p)^{m-\ell }\qquad {\text{mit }}m:=n-1\\&=np\left(p+\left(1-p\right)\right)^{m}=np1^{m}=np.\end{aligned}}$

Alternativ kann man verwenden, dass eine $B(\cdot \mid p,n)$-verteilte Zufallsvariable $X$ als eine Summe von $n$ unabhängigen Bernoulli-verteilten Zufallsvariablen $X_{i}$ mit $\operatorname {E} (X_{i})=p$ geschrieben werden kann. Mit der Linearität des Erwartungswertes folgt dann

$\operatorname {E} (X)=\operatorname {E} (X_{1}+\dotsb +X_{n})=\operatorname {E} (X_{1})+\dotsb +\operatorname {E} (X_{n})=np.$

Alternativ kann man ebenfalls mit Hilfe des binomischen Lehrsatzes folgenden Beweis geben: Differenziert man bei der Gleichung

$(a+b)^{n}=\sum _{k=0}^{n}{\tbinom {n}{k}}a^{k}b^{n-k}$

beide Seiten nach $a$, ergibt sich

$n(a+b)^{n-1}=\sum _{k=0}^{n}k{\tbinom {n}{k}}a^{k-1}b^{n-k}$,

also

$na(a+b)^{n-1}=\sum _{k=0}^{n}k{\tbinom {n}{k}}a^{k}b^{n-k}$.

Mit $a=p$ und $b=1-p$ folgt das gewünschte Ergebnis.

Varianz

Eine binomialverteilte Zufallsvariable $X\sim B(n,p)$ besitzt die Varianz $\mathrm {Var} [X]=np(1-p)$.

Beweis

Es sei $X$ eine $B(n,p)$-verteilte Zufallsvariable. Die Varianz bestimmt sich direkt aus dem Verschiebungssatz $\operatorname {Var} [X]=\operatorname {E} [X^{2}]-\left(\operatorname {E} [X]\right)^{2}$ zu

${\begin{aligned}\operatorname {Var} [X]&=\sum _{k=0}^{n}k^{2}\cdot P(X=k)-(np)^{2}\\&=\sum _{k=0}^{n}k^{2}\cdot {n \choose k}p^{k}(1-p)^{n-k}-n^{2}p^{2}\\&={\cancel {n^{2}p^{2}}}-np^{2}+np{\cancel {-n^{2}p^{2}}}\\&=np(1-p)\end{aligned}}$

oder alternativ aus der Gleichung von Bienaymé, angewendet auf die Varianz unabhängiger Zufallsvariablen, wenn man berücksichtigt, dass die identisch verteilten Zufallsvariablen $X_{i}$ der Bernoulli-Verteilung mit $\operatorname {Var} [X_{i}]=p(1-p)$ genügen, zu

$\operatorname {Var} [X]=\operatorname {Var} [X_{1}+\dots +X_{n}]=\operatorname {Var} [X_{1}]+\dots +\operatorname {Var} [X_{n}]=n\operatorname {Var} [X_{1}]=np(1-p).$

Die zweite Gleichheit gilt, weil die Einzelexperimente unabhängig sind, sodass die Einzelvariablen unkorreliert sind.

Variationskoeffizient

Aus Erwartungswert und Varianz erhält man den Variationskoeffizienten

$\operatorname {VarK} (X)={\sqrt {\frac {1-p}{np}}}.$

Schiefe

Die Schiefe ergibt sich zu

$\operatorname {v} (X)={\frac {1-2p}{\sqrt {np(1-p)}}}.$

Wölbung

Die Wölbung lässt sich ebenfalls geschlossen darstellen als

$\beta _{2}=3+{\frac {1-6p(1-p)}{np(1-p)}}.$

Damit ist der Exzess

$\gamma _{2}={\frac {1-6p(1-p)}{np(1-p)}}.$

Modus

Der Modus, also der Wert mit der maximalen Wahrscheinlichkeit, ist für $p<1$ gleich $k=\lfloor np+p\rfloor$ und für $p=1$ gleich $n$. Falls $np+p$ eine natürliche Zahl ist, ist $k=np+p-1$ ebenfalls ein Modus. Falls der Erwartungswert eine natürliche Zahl ist, ist der Erwartungswert gleich dem Modus.

Beweis

Sei ohne Einschränkung $0<p<1$. Wir betrachten den Quotienten

$\alpha _{k}:={\frac {B(k+1\mid p,n)}{B(k\mid p,n)}}={\frac {\,{\frac {n!}{(k+1)!(n-k-1)!}}\,}{\frac {n!}{k!(n-k)!}}}\cdot {\frac {p^{k+1}(1-p)^{n-k-1}}{p^{k}(1-p)^{n-k}}}={\frac {n-k}{k+1}}\cdot {\frac {p}{1-p}}$.

Nun gilt $\alpha _{k}>1$, falls $k<np+p-1$ und $\alpha _{k}<1$, falls $k>np+p-1$. Also:

${\begin{aligned}k>(n+1)p-1\Rightarrow \alpha _{k}<1\Rightarrow B(k+1\mid p,n)<B(k\mid p,n)\\k=(n+1)p-1\Rightarrow \alpha _{k}=1\Rightarrow B(k+1\mid p,n)=B(k\mid p,n)\\k<(n+1)p-1\Rightarrow \alpha _{k}>1\Rightarrow B(k+1\mid p,n)>B(k\mid p,n)\end{aligned}}$

Und nur im Fall $np+p-1\in \mathbb {N}$ hat der Quotient den Wert 1, d. h. $B(np+p-1\mid n,p)=B(np+p\mid n,p)$.

Median

Es ist nicht möglich, eine allgemeine Formel für den Median der Binomialverteilung anzugeben. Daher sind verschiedene Fälle zu betrachten, die einen geeigneten Median liefern:

• Ist $np$ eine natürliche Zahl, dann stimmen Erwartungswert, Median und Modus überein und sind gleich $np$.
• Ein Median $m$ liegt im Intervall $\lfloor np\rfloor \leq m\leq \lceil np\rceil$. Hierbei bezeichnen $\lfloor \cdot \rfloor$ die Abrundungsfunktion und $\lceil \cdot \rceil$ die Aufrundungsfunktion.
• Ein Median $m$ kann nicht zu stark vom Erwartungswert abweichen: $|m-np|\leq \min\{\ln 2,\max\{p,1-p\}\}$.
• Der Median ist eindeutig und stimmt mit $m=$ round$(np)$ überein, wenn entweder $p\leq 1-\ln 2$ oder $p\geq \ln 2$ oder $|m-np|\leq \min\{p,1-p\}$ (außer wenn $p=1/2$ und $n$ gerade ist).
• Ist $p=1/2$ und $n$ ungerade, so ist jede Zahl $m$ im Intervall $1/2(n-1)\leq m\leq 1/2(n+1)$ ein Median der Binomialverteilung mit Parametern $p$ und $n$. Ist $p=1/2$ und $n$ gerade, so ist $m=n/2$ der eindeutige Median.

Kumulanten

Analog zur Bernoulli-Verteilung ist die kumulantenerzeugende Funktion

$g_{X}(t)=n\ln(pe^{t}+q)$.

Damit sind die ersten Kumulanten $\kappa _{1}=np,\kappa _{2}=npq$ und es gilt die Rekursionsgleichung

$\kappa _{k+1}=p(1-p){\frac {d\kappa _{k}}{dp}}.$

Charakteristische Funktion

Die charakteristische Funktion hat die Form

$\phi _{X}(s)=\left(\left(1-p\right)+p\mathrm {e} ^{\mathrm {i} s}\right)^{n}=\left(q+p\mathrm {e} ^{\mathrm {i} s}\right)^{n}.$

Wahrscheinlichkeitserzeugende Funktion

Für die wahrscheinlichkeitserzeugende Funktion erhält man

$g_{X}(s)=(ps+(1-p))^{n}.$

Momenterzeugende Funktion

Die momenterzeugende Funktion der Binomialverteilung lautet

${\begin{aligned}m_{X}(s)&=\operatorname {E} \left(e^{sX}\right)\\&=\sum _{k=0}^{n}\mathrm {e} ^{sk}\cdot {\binom {n}{k}}p^{k}(1-p)^{n-k}\\&=\sum _{k=0}^{n}{\binom {n}{k}}(\mathrm {e} ^{s}p)^{k}(1-p)^{n-k}\\&=\left(p\cdot \mathrm {e} ^{s}+\left(1-p\right)\right)^{n}.\end{aligned}}$

Summe binomialverteilter Zufallsgrößen

Für die Summe $Z=X+Y$ zweier unabhängiger binomialverteilter Zufallsgrößen $X$ und $Y$ mit den Parametern $n_{1}$, $p$ und $n_{2}$, $p$ erhält man die Einzelwahrscheinlichkeiten durch Anwendung der Vandermondeschen Identität

${\begin{aligned}\operatorname {P} (Z=k)&=\sum _{i=0}^{k}\left[{\binom {n_{1}}{i}}p^{i}(1-p)^{n_{1}-i}\right]\left[{\binom {n_{2}}{k-i}}p^{k-i}(1-p)^{n_{2}-k+i}\right]\\&={\binom {n_{1}+n_{2}}{k}}p^{k}(1-p)^{n_{1}+n_{2}-k}\qquad (k=0,1,\dotsc ,n_{1}+n_{2}),\end{aligned}}$

also wieder eine binomialverteilte Zufallsgröße, jedoch mit den Parametern $n_{1}+n_{2}$ und $p$. Somit gilt für die Faltung

$\operatorname {Bin} (n,p)*\operatorname {Bin} (m,p)=\operatorname {Bin} (n+m,p)$

Die Binomialverteilung ist also reproduktiv für festes $p$ bzw. bildet eine Faltungshalbgruppe.

Wenn die Summe $Z=X+Y$ bekannt ist, folgt jede der Zufallsvariablen $X$ und $Y$ unter dieser Bedingung einer hypergeometrischen Verteilung. Dazu berechnet man die bedingte Wahrscheinlichkeit:

${\begin{aligned}P(X=\ell |Z=k)&={\frac {P(X=\ell \cap Z=k)}{P(Z=k)}}\\&={\frac {P(X=\ell \cap Y=k-\ell )}{P(Z=k)}}\\&={\frac {P(X=\ell )P(Y=k-\ell )}{P(Z=k)}}\\&={\frac {{\binom {n_{1}}{\ell }}p^{\ell }(1-p)^{n_{1}-\ell }{\binom {n_{2}}{k-\ell }}p^{k-\ell }(1-p)^{n_{2}-k+\ell }}{{\binom {n_{1}+n_{2}}{k}}p^{k}(1-p)^{n_{1}+n_{2}-k}}}\\&={\frac {{\binom {n_{1}}{\ell }}{\binom {n_{2}}{k-\ell }}}{\binom {n_{1}+n_{2}}{k}}}\\&=h(\ell ;n_{1}+n_{2};n_{1};k)\end{aligned}}$

Dies stellt eine hypergeometrische Verteilung dar.

Allgemein gilt: Wenn die $m$ Zufallsvariablen $X_{i}$ stochastisch unabhängig sind und den Binomialverteilungen $B(n_{i},p)$ genügen, dann ist auch die Summe $X_{1}+X_{2}+\dotsb +X_{m}$ binomialverteilt, jedoch mit den Parametern $n_{1}+n_{2}+\dotsb +n_{m}$ und $p$. Addiert man binomialverteilte Zufallsvariablen $X_{1},X_{2}$ mit $p_{1}\neq p_{2}$, dann erhält man eine verallgemeinerte Binomialverteilung.

Beziehung zu anderen Verteilungen

Beziehung zur Bernoulli-Verteilung

Ein Spezialfall der Binomialverteilung für $n=1$ ist die Bernoulli-Verteilung. Die Summe von unabhängigen und identischen Bernoulli-verteilten Zufallsgrößen genügt demnach der Binomialverteilung.

Beziehung zur verallgemeinerten Binomialverteilung

Die Binomialverteilung ist ein Spezialfall der verallgemeinerten Binomialverteilung mit $p_{i}=p_{j}$ für alle $i,j\in \{1,\dotsc ,n\}$. Genauer ist sie für festen Erwartungswert und feste Ordnung diejenige verallgemeinerte Binomialverteilung mit maximaler Entropie.

Übergang zur Normalverteilung

Nach dem Satz von Moivre-Laplace konvergiert die Binomialverteilung im Grenzfall $n\to \infty$ gegen eine Normalverteilung, d. h., die Normalverteilung kann als brauchbare Näherung der Binomialverteilung verwendet werden, wenn der Stichprobenumfang hinreichend groß und der Anteil der gesuchten Ausprägung nicht zu klein ist. Mit dem Galtonbrett kann man die Annäherung an die Normalverteilung experimentell nachempfinden.

Es gilt $\mu =np$ und $\sigma ^{2}=npq.$ Durch Einsetzen in die Verteilungsfunktion $\Phi$ der Standardnormalverteilung folgt

$B(k\mid p,n)\approx \Phi \left({k+0{,}5-np \over {\sqrt {npq}}}\right)-\ \Phi \left({k-0{,}5-np \over {\sqrt {npq}}}\right)\approx {1 \over {\sqrt {npq}}}\cdot \ {\frac {1}{\sqrt {2\pi }}}\,\cdot \ \exp \left(-{{(k-np)}^{2} \over 2npq}\right).$

Wie zu sehen, ist das Ergebnis damit nichts anderes als der Funktionswert der Normalverteilung für $x=k$, $\mu =n\cdot p$ sowie $\sigma ^{2}=n\cdot p\cdot q$ (den man sich anschaulich auch als Flächeninhalt des $k$-ten Streifens des Histogramms der standardisierten Binomialverteilung mit $1/\sigma$ als dessen Breite sowie $\Phi ((k-\mu )/\sigma )$ als dessen Höhe vorstellen kann). Die Annäherung der Binomialverteilung an die Normalverteilung wird bei der Normal-Approximation genutzt, um schnell die Wahrscheinlichkeit vieler Stufen der Binomialverteilung zu bestimmen, zumal dann, wenn für diese keine Tabellenwerte (mehr) vorliegen.

Übergang zur Poisson-Verteilung

Eine asymptotisch asymmetrische Binomialverteilung, deren Erwartungswert $np$ für $n\rightarrow \infty$ und $p\rightarrow 0$ gegen eine Konstante $\lambda$ konvergiert, kann man durch die Poisson-Verteilung annähern. Der Wert $\lambda$ ist dann für alle in der Grenzwertbildung betrachteten Binomialverteilungen wie auch für die resultierende Poisson-Verteilung der Erwartungswert. Diese Annäherung wird auch als Poisson-Approximation, Poissonscher Grenzwertsatz oder als das Gesetz seltener Ereignisse bezeichnet.

${\begin{aligned}B(k\mid p,n)&={n \choose k}p^{k}\,(1-p)^{n-k}={\frac {n!}{(n-k)!\,k!}}\left({\frac {np}{n}}\right)^{k}\left(1-{\frac {np}{n}}\right)^{n-k}\\&={\frac {n(n-1)(n-2)\dotsm (n-k+1)}{n^{k}}}\,{\frac {(np)^{k}}{k!}}\left(1-{\frac {np}{n}}\right)^{n-k}\\&=\left(1-{\frac {1}{n}}\right)\left(1-{\frac {2}{n}}\right)\dotsm \left(1-{\frac {k-1}{n}}\right){\frac {(np)^{k}}{k!}}\left(1-{\frac {(np)}{n}}\right)^{n-k}\\&\to \,{\frac {\lambda ^{k}}{k!}}\mathrm {e} ^{-\lambda },\quad {\text{mit}}\quad \lambda =n\cdot {}p\quad {\text{wenn}}\quad n\to \infty \quad {\text{und}}\quad p\rightarrow 0\end{aligned}}$

Eine Faustregel besagt, dass diese Näherung brauchbar ist, wenn $n\geq 50$ und $p\leq 0{,}05$.

Die Poisson-Verteilung ist also die Grenzverteilung der Binomialverteilung für große $n$ und kleine $p$, es handelt sich hierbei um Konvergenz in Verteilung.

Beziehung zur geometrischen Verteilung

Die Zahl der Misserfolge bis zum erstmaligen Eintritt eines Erfolgs wird durch die geometrische Verteilung beschrieben.

Beziehung zur negativen Binomialverteilung

Die negative Binomialverteilung hingegen beschreibt die Wahrscheinlichkeitsverteilung der Anzahl der Versuche, die erforderlich sind, um in einem Bernoulli-Prozess eine vorgegebene Anzahl von Erfolgen zu erzielen. In der Tabelle werden beide Verteilungen veranschaulicht:

	Deterministisch	Zufällig	Fragestellung
Binomialverteilung	$n$ Versuche	$X$ Erfolge	Wie viele Erfolge $X$ haben wir in $n$ Versuchen?
Negative Binomialverteilung	$x$ Erfolge	$N$ Versuche	Wie viele Versuche $N$ sind erforderlich, um $x$ Erfolge zu haben?

Beziehung zur hypergeometrischen Verteilung

Bei der Binomialverteilung werden die ausgewählten Stichproben wieder in die Auswahlmenge zurückgeführt, können also zu einem späteren Zeitpunkt erneut ausgewählt werden. Werden im Gegensatz dazu die Stichproben nicht in die Grundgesamtheit zurückgegeben, kommt die hypergeometrische Verteilung zur Anwendung. Die beiden Verteilungen gehen bei großem Umfang $N$ der Grundgesamtheit und geringem Umfang $n$ der Stichproben ineinander über. Als Faustregel gilt, dass für $n/N\leq 0{,}05$ auch bei Nichtzurücklegen der Stichproben die Binomialverteilung statt der mathematisch anspruchsvolleren hypergeometrischen Verteilung verwendet werden kann, da beide in diesem Fall nur unwesentlich voneinander abweichende Ergebnisse liefern.

Beziehung zur Multinomialverteilung

Die Binomialverteilung ist ein Spezialfall der Multinomialverteilung.

Beziehung zur Rademacher-Verteilung

Ist $Y$ Binomialverteilt zum Parameter $p=0{,}5$ und $n$, so lässt sich $Y$ als skalierte Summe von $n$ Rademacher-verteilten Zufallsvariablen $X_{1},\dotsc ,X_{n}$ darstellen:

$Y=0{,}5\left(n+\sum _{i=1}^{n}X_{i}\right)$

Dies wird insbesondere beim symmetrischen Random Walk auf $\mathbb {Z}$ verwendet.

Beziehung zur Panjer-Verteilung

Die Binomialverteilung ist ein Spezialfall der Panjer-Verteilung, welche die Verteilungen Binomialverteilung, Negative Binomialverteilung und Poisson-Verteilung in einer Verteilungsklasse vereint.

Beziehung zur Betaverteilung

Für viele Anwendungen ist es nötig, die Verteilungsfunktion

$\sum _{i=0}^{k}B(i\mid p,n)$

konkret auszurechnen (beispielsweise bei statistischen Tests oder für Konfidenzintervalle).

Hier hilft die folgende Beziehung zur Betaverteilung:

$\sum _{i=0}^{k}{\binom {n}{i}}\cdot p^{i}\cdot (1-p)^{n-i}=\operatorname {Beta} (1-p;n-k;k+1)$

Diese lautet für ganzzahlige positive Parameter $a$ und $b$:

$\operatorname {Beta} (x;a;b)={(a+b-1)! \over (a-1)!\cdot (b-1)!}\int _{0}^{x}u^{a-1}(1-u)^{b-1}\,\mathrm {d} u$

Um die Gleichung

$\sum _{i=0}^{k}{\binom {n}{i}}\cdot p^{i}\cdot (1-p)^{n-i}={n! \over (n-k-1)!\cdot k!}\int _{0}^{1-p}u^{n-k-1}(1-u)^{k}\,\mathrm {d} u$

zu beweisen, kann man folgendermaßen vorgehen:

• Die linke und rechte Seite stimmen für $p=0$ überein (beide Seiten sind gleich 1).
• Die Ableitungen nach $p$ stimmen für die linke und rechte Seite der Gleichung überein, sie sind nämlich beide gleich $-{n! \over (n-k-1)!\cdot k!}\cdot p^{k}\cdot (1-p)^{n-k-1}$.

Beziehung zur Beta-Binomialverteilung

Eine Binomialverteilung, deren Parameter $p$ Beta-verteilt ist, nennt man eine Beta-Binomialverteilung. Sie ist eine Mischverteilung.

Beziehung zur Pólya-Verteilung

Die Binomialverteilung ist ein Spezialfall der Pólya-Verteilung (wähle $c=0$).

Beispiele

Symmetrische Binomialverteilung (p = 1/2)

• 
  p = 0,5 und n = 4, 16, 64
• 
  Mittelwert abgezogen
• 
  Skalierung mit Standardabweichung

Dieser Fall tritt auf beim $n$-fachen Münzwurf mit einer fairen Münze (Wahrscheinlichkeit für Kopf gleich der für Zahl, also gleich 1/2). Die erste Abbildung zeigt die Binomialverteilung für $p=0{,}5$ und für verschiedene Werte von $n$ als Funktion von $k$. Diese Binomialverteilungen sind spiegelsymmetrisch um den Wert $k=n/2$:

Binomialverteilungen mit p = 0,5 (mit Verschiebung um −n/2 und Skalierung) für n = 4, 6, 8, 12, 16, 23, 32, 46

Die gleichen Daten in halblogarithmischer Auftragung

$B(k\mid 1/2;n)=B(n-k\mid 1/2;n)$

Dies ist in der zweiten Abbildung veranschaulicht. Die Breite der Verteilung wächst proportional zur Standardabweichung $\sigma ={\frac {\sqrt {n}}{2}}$. Der Funktionswert bei $k=n/2$, also das Maximum der Kurve, sinkt proportional zu $\sigma$.

Dementsprechend kann man Binomialverteilungen mit unterschiedlichem $n$ aufeinander skalieren, indem man die Abszisse $k-n/2$ durch $\sigma$ teilt und die Ordinate mit $\sigma$ multipliziert (dritte Abbildung oben).

Die nebenstehende Graphik zeigt noch einmal reskalierte Binomialverteilungen, nun für andere Werte von $n$ und in einer Auftragung, die besser verdeutlicht, dass sämtliche Funktionswerte mit steigendem $n$ gegen eine gemeinsame Kurve konvergieren. Indem man die Stirling-Formel auf die Binomialkoeffizienten anwendet, erkennt man, dass diese Kurve (im Bild schwarz durchgezogen) eine Gaußsche Glockenkurve ist:

$f(x)={\frac {1}{\sqrt {2\pi }}}\,{\mathrm {e} }^{-{\frac {x^{2}}{2}}}$.

Dies ist die Wahrscheinlichkeitsdichte zur Standardnormalverteilung ${\mathcal {N}}(0,1)$. Im zentralen Grenzwertsatz wird dieser Befund so verallgemeinert, dass auch Folgen anderer diskreter Wahrscheinlichkeitsverteilungen gegen die Normalverteilung konvergieren.

Die zweite nebenstehende Graphik zeigt die gleichen Daten in einer halblogarithmischen Auftragung. Dies ist dann zu empfehlen, wenn man überprüfen möchte, ob auch seltene Ereignisse, die um mehrere Standardabweichungen vom Erwartungswert abweichen, einer Binomial- oder Normalverteilung folgen.

Ziehen von Kugeln

In einem Behälter befinden sich 80 Kugeln, davon sind 16 gelb. Es wird 5-mal eine Kugel entnommen und anschließend wieder zurückgelegt. Wegen des Zurücklegens ist die Wahrscheinlichkeit, eine gelbe Kugel zu ziehen, bei allen Entnahmen gleich groß, und zwar 16/80 = 1/5. Der Wert $B\left(k\mid {\tfrac {1}{5}};5\right)$ gibt die Wahrscheinlichkeit dafür an, dass genau $k$ der entnommenen Kugeln gelb sind. Als Beispiel rechnen wir $k=3$:

$B\left(3\mid {\tfrac {1}{5}};5\right)={\binom {5}{3}}\cdot \left({\frac {1}{5}}\right)^{3}\cdot \left({\frac {4}{5}}\right)^{2}={\frac {5\cdot 4}{1\cdot 2}}\cdot {\frac {1}{125}}\cdot {\frac {16}{25}}={\frac {64}{1250}}=0{,}0512$

In ungefähr 5 % der Fälle zieht man also genau 3 gelbe Kugeln.

B(k | 0,2; 5)
k	Wahrscheinlichkeit in %
0	0032,768
1	0040,96
2	0020,48
3	0005,12
4	0000,64
5	0000,032
∑	0100
Erw.Wert	0001
Varianz	0000.8

Anzahl der Personen mit Geburtstag am Wochenende

Die Wahrscheinlichkeit, dass eine Person in diesem Jahr an einem Wochenende Geburtstag hat, betrage (der Einfachheit halber) 2/7. In einem Raum halten sich 10 Personen auf. Der Wert $B(k\mid 2/7;10)$ gibt (im vereinfachten Modell) die Wahrscheinlichkeit dafür an, dass genau $k$ der Anwesenden in diesem Jahr an einem Wochenende Geburtstag haben.

B(k | 2/7; 10)
k	Wahrscheinlichkeit in % (gerundet)
0	0003,46
1	0013,83
2	0024,89
3	0026,55
4	0018,59
5	0008,92
6	0002,97
7	0000,6797
8	0000,1020
9	0000,009063
10	0000,0003625
∑	0100
Erw.Wert	0002,86
Varianz	0002,04

Gemeinsamer Geburtstag im Jahr

253 Personen sind zusammengekommen. Der Wert $B(k\mid 1/365;253)$ gibt die Wahrscheinlichkeit an, dass genau $k$ Anwesende an einem zufällig gewählten Tag Geburtstag haben (ohne Beachtung des Jahrganges).

B(k | 1/365; 253)
k	Wahrscheinlichkeit in % (gerundet)
0	049,95
1	034,72
2	012,02
3	002,76
4	000,47

Die Wahrscheinlichkeit, dass „irgendjemand“ dieser 253 Personen, d. h. eine oder mehrere Personen, an diesem Tag Geburtstag hat, beträgt somit $1-B(0\mid 1/365;253)=50.05\,\%$.

Bei 252 Personen beträgt die Wahrscheinlichkeit $1-B(0\mid 1/365;252)=49.91\,\%$. Das heißt, die Schwelle der Anzahl von Personen, ab der die Wahrscheinlichkeit, dass mindestens eine dieser Personen an einem zufällig gewählten Tag Geburtstag hat, größer als 50 % wird, beträgt 253 Personen (siehe dazu auch Geburtstagsparadoxon).

Die direkte Berechnung der Binomialverteilung kann aufgrund der großen Fakultäten schwierig sein. Eine Näherung über die Poisson-Verteilung ist hier zulässig ($n>50,p<0{,}05$). Mit dem Parameter $\lambda =np=253/365$ ergeben sich folgende Werte:

P253/365(k)
k	Wahrscheinlichkeit in % (gerundet)
0	050
1	034,66
2	012,01
3	002,78
4	000,48

Konfidenzintervall für eine Wahrscheinlichkeit

In einer Meinungsumfrage unter $n$ Personen geben $k$ Personen an, die Partei A zu wählen. Bestimme ein 95-%-Konfidenzintervall für den unbekannten Anteil der Wähler, die Partei A wählen, in der Gesamtwählerschaft.

Eine Lösung des Problems ohne Rückgriff auf die Normalverteilung findet sich im Artikel Konfidenzintervall für die Erfolgswahrscheinlichkeit der Binomialverteilung.

Auslastungsmodell

Mittels folgender Formel lässt sich die Wahrscheinlichkeit dafür errechnen, dass $k$ von $n$ Personen eine Tätigkeit, die durchschnittlich $m$ Minuten pro Stunde dauert, gleichzeitig ausführen.

$P(X=k)={n \choose k}\cdot \left({\frac {m}{60}}\right)^{k}\cdot \left(1-{\frac {m}{60}}\right)^{n-k}$

Statistischer Fehler der Klassenhäufigkeit in Histogrammen

Die Darstellung unabhängiger Messergebnisse in einem Histogramm führt zur Gruppierung der Messwerte in Klassen.

Die Wahrscheinlichkeit für $n_{i}$ Einträge in Klasse $i$ ist gegeben durch die Binomialverteilung

$B_{n,p_{i}}(n_{i})$ mit $n=\sum n_{i}$ und $p_{i}={\frac {n_{i}}{n}}$.

Erwartungswert und Varianz der $n_{i}$ sind dann

$E(n_{i})=np_{i}=n_{i}$ und $V(n_{i})=np_{i}(1-p_{i})=n_{i}\left(1-{\frac {n_{i}}{n}}\right)$.

Damit liegt der statistische Fehler der Anzahl von Einträgen in Klasse $i$ bei

$\sigma (n_{i})={\sqrt {n_{i}\left(1-{\frac {n_{i}}{n}}\right)}}$.

Bei großer Zahl von Klassen wird $p_{i}$ klein und $\sigma (n_{i})\approx {\sqrt {n_{i}}}$.

So lässt sich beispielsweise die statistische Genauigkeit von Monte-Carlo-Simulationen bestimmen.

Zufallszahlen

Zufallszahlen zur Binomialverteilung werden üblicherweise mit Hilfe der Inversionsmethode erzeugt.

Alternativ kann man auch ausnutzen, dass die Summe von Bernoulli-verteilten Zufallsvariablen binomialverteilt ist. Dazu erzeugt man $n$ Bernoulli-verteilte Zufallszahlen und summiert sie auf; das Ergebnis ist eine binomialverteilte Zufallszahl.

Bezeichnungen

Der Aufruf der Wahrscheinlichkeitsfunktion der Binomialverteilung bei Taschenrechnern und Mathematischer Software geschieht meistens mit binom, pdfbin oder Binomialpdf (Binomial probability density function). Die kumulierte Verteilungsfunktion wird mit cdfbin oder Binomialcdf (Binomial cumulative distribution function) abgekürzt.

Weblinks

Commons: Binomialverteilung – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Binomialverteilung – Lern- und Lehrmaterialien

Wikibooks: ${\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}$ – Mathematik für die Schule

• Bernoulli-Versuche und Binomialverteilung
• Rechner für einfache und kumulierte Wahrscheinlichkeiten der Binomialverteilung
• Berechnung der Binomialverteilung für einfache und kumulierte Wahrscheinlichkeiten (englisch)
• Umfangreiches Tabellenwerk (PDF; 10 MB)
• Binomial- und Normalverteilung – Online-Lehrgang mit dynamischen Arbeitsblättern (Java-Plugin benötigt)
• Interaktive Simulation Münzwurf – inkl. Aufgabenstellungen (HTML5 ohne Plugin)
• Interaktive Animation – Universität Konstanz (Java-Plugin benötigt)
• Interaktive Animation (Flash-Plugin benötigt)
• Earliest Known Uses of Some of the Words of Probability & Statistics – Kees Verduin.
• Lernvideo für die Oberstufe
• Statistische Fehler (Ausführliche Erläuterung aus der Universität Ulm)

Einzelnachweise

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | Dirac | diskret uniform | empirisch | hypergeometrisch | kategorial | negativ hypergeometrisch | Rademacher | verallgemeinert binomial | Zipf | Zipf-Mandelbrot | Zweipunkt

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | discrete-Phase-Type | erweitert negativ binomial | Gauss-Kuzmin | gemischt Poisson | geometrisch | logarithmisch | negativ binomial | parabolisch-fraktal | Poisson | Skellam | verallgemeinert Poisson | Yule-Simon | Zeta

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Cantor | Kumaraswamy | raised Cosine | Dreieck | Trapez | U-quadratisch | stetig uniform | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi | Chi-Quadrat | Coxian | Erlang | Exponential | Extremwert | F | Fermi-Dirac | Folded normal | Fréchet | Gamma | Gamma-Gamma | verallgemeinert invers Gauß | halblogistisch | halbnormal | Hartman-Watson | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | invers Chi-Quadrat | scale-invers Chi-Quadrat | Invers Normal | Invers Gamma | Kolmogorow-Verteilung | Lévy | log-normal | log-logistisch | Maxwell-Boltzmann | Maxwell-Speed | Nakagami | nichtzentriert Chi-Quadrat | Pareto | Phase-Type | Rayleigh | relativistisch Breit-Wigner | Rice | Rosin-Rammler | shifted Gompertz | truncated normal | Type-2-Gumbel | Weibull | Wilks’ Lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | exponential Power | Fishers z | Fisher-Tippett (Gumbel) | generalized hyperbolic | Hyperbolic-secant | Landau | Laplace | alpha-stabil | logistisch | normal (Gauß) | normal-invers Gauß’sch | Skew-normal | Studentsche t | Type-1-Gumbel | Variance-Gamma | Voigt

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Dirichlet compound multinomial | Ewens | gemischt Multinomial | multinomial | multivariat hypergeometrisch | multivariat Poisson | negativmultinomial | Pólya/Eggenberger | polyhypergeometrisch

Kontinuierliche multivariate Verteilungen:
Dirichlet | GEM | generalized Dirichlet | multivariat normal | multivariat Student | normalskaliert invers Gamma | Normal-Gamma | Poisson-Dirichlet

Multivariate Matrixverteilungen:
Gleichverteilung auf der Stiefel-Mannigfaltigkeit | Invers Wishart | Matrix Beta | Matrix Gamma | Matrix invers Beta | Matrix invers Gamma | Matrix Normal | Matrix Student-t | Matrix-Von-Mises-Fisher-Verteilung | Normal-invers-Wishart | Normal-Wishart | Wishart