Bernoulli-Verteilung

Zufallsvariablen mit einer Bernoulli-Verteilung (auch als Bernoullische Verteilung^[1], Null-Eins-Verteilung^[1], Alternativ-Verteilung^[2] oder Boole-Verteilung^[3] bezeichnet) benutzt man zur Beschreibung von zufälligen Ereignissen, bei denen es nur zwei mögliche Versuchsausgänge gibt. Einer der Versuchsausgänge wird meistens mit Erfolg bezeichnet und der komplementäre Versuchsausgang mit Misserfolg. Die zugehörige Wahrscheinlichkeit $p$ für einen Erfolg nennt man Erfolgswahrscheinlichkeit und $q=1-p$ die Wahrscheinlichkeit eines Misserfolgs. Beispiele:

Werfen einer Münze: Kopf (Erfolg), $p=1/2$ , und Zahl (Misserfolg), $q=1/2$ .
Werfen eines Würfels, wobei nur eine „6“ als Erfolg gewertet wird: $p=1/6$ , $q=5/6$ .
Betrachte sehr kleines Raum/Zeit-Intervall: Ereignis tritt ein $(p\gtrapprox 0)$ , tritt nicht ein $(q\lessapprox 1)$ .

Die Bezeichnung Bernoulli-Versuch (Bernoullian trials nach Jakob I Bernoulli) wurde erstmals 1937 in dem Buch Introduction to Mathematical Probability von James Victor Uspensky verwendet.^[4]

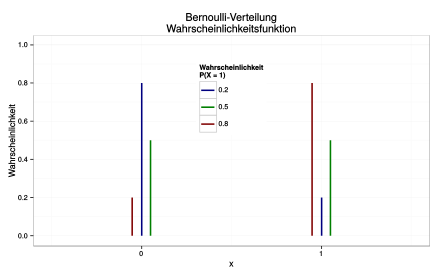
Definition Bearbeiten

Eine diskrete Zufallsgröße $X$ mit Werten in der Menge $\{0,1\}$ unterliegt der Bernoulli-Verteilung oder Null-Eins-Verteilung mit dem Parameter $p\in (0,1)$ , wenn sie der folgenden Wahrscheinlichkeitsfunktion folgt

f(x)=P(X=x)={\begin{cases}1-p&{\text{falls}}\quad x=0,\\p&{\text{falls}}\quad x=1,\\0&{\text{sonst.}}\end{cases}}

Die Verteilungsfunktion ist dann

F(x)=P(X\leq x)={\begin{cases}0&{\text{ falls }}\quad x<0\\1-p&{\text{ falls }}\quad 0\leq x<1\\1&{\text{ falls }}\quad x\geq 1\end{cases}}

.

Man schreibt dann $X\sim {\mathcal {B}}(p)$ , $X\sim \mathrm {Ber} (p)$ oder $X\sim Ber_{p}$ . Der Parameter $p$ heißt in diesem Zusammenhang auch Bernoulli-Parameter.

Eine Zufallsvariable, deren Verteilung eine Bernoulli-Verteilung ist, heißt Bernoulli-verteilt. Eine Bernoulli-verteilte Zufallsvariable wird auch als Bernoulli-Variable bezeichnet.

Ein Zufallsexperiment, dessen Ausgang durch eine Bernoulli-Variable beschrieben ist, heißt Bernoulli-Experiment oder Bernoulli-Versuch. Eine Folge von Bernoulli-Versuchen, deren Zufallsvariablen stochastisch unabhängig und identisch – d. h. mit demselben Bernoulli-Parameter – verteilt sind, heißt Bernoulli-Prozess oder bernoullisches Versuchsschema.

Für bestimmte statistische Anwendungen ist es sinnvoll, den erweiterten Parameterraum $[0,1]$ ergänzt durch die beiden Grenzfälle $p=0$ und $p=1$ zugrunde zu legen, bei denen die Bernoulli-Verteilung zu einer Einpunktverteilung auf 0 oder 1 degeneriert. In diesen Fällen gilt $P(X=0)=1$ bzw. $P(X=1)=1$ .

Eigenschaften Bearbeiten

Im Folgenden ist $X\sim \mathrm {Ber} (p)$ mit $0<p<1$ vorausgesetzt.

Erwartungswert Bearbeiten

Die Bernoulli-Verteilung mit Parameter $p$ hat den Erwartungswert:

\operatorname {E} \left(X\right)=p

Dies hat den Grund, dass für eine Bernoulli-verteilte Zufallsvariable $X$ mit $P(X=1)=p$ und $P(X=0)=q$ gilt:

\operatorname {E} (X)=P(X=1)\cdot 1+P(X=0)\cdot 0=p\cdot 1+q\cdot 0=p

Varianz und weitere Streumaße Bearbeiten

Die Bernoulli-Verteilung besitzt die Varianz

\operatorname {Var} (X)=p\cdot (1-p)=pq

denn es ist $\operatorname {E} (X^{2})=p\cdot 1^{2}+q\cdot 0^{2}=p$ und damit

\operatorname {E} \left(X^{2}\right)-\operatorname {E} (X)^{2}=p-p^{2}=p\cdot (1-p)=pq

.

Damit ist die Standardabweichung

\sigma _{X}={\sqrt {pq}}

und der Variationskoeffizient

\operatorname {VarK} (X)={\sqrt {\frac {q}{p}}}

.

Symmetrie Bearbeiten

Für den Parameter $p={\tfrac {1}{2}}$ ist die Bernoulli-Verteilung symmetrisch um den Punkt $a={\tfrac {1}{2}}$ .

Schiefe Bearbeiten

Die Schiefe der Bernoulli-Verteilung ist

\operatorname {v} (X)={\frac {1-2p}{\sqrt {pq}}}

.

Dies kann folgendermaßen gezeigt werden. Eine standardisierte Zufallsvariable ${\frac {X-\operatorname {E} (X)}{\sqrt {\operatorname {Var} (X)}}}$ mit $X$ Bernoulli-verteilt nimmt den Wert ${\frac {q}{\sqrt {pq}}}$ mit Wahrscheinlichkeit $p$ an und den Wert $-{\frac {p}{\sqrt {pq}}}$ mit Wahrscheinlichkeit $q$ . Damit erhalten wir für die Schiefe

{\begin{aligned}\operatorname {v} (X)&=\operatorname {E} \left[\left({\frac {X-\operatorname {E} (X)}{\sqrt {\operatorname {Var} (X)}}}\right)^{3}\right]\\&=p\cdot \left({\frac {q}{\sqrt {pq}}}\right)^{3}+q\cdot \left(-{\frac {p}{\sqrt {pq}}}\right)^{3}\\&={\frac {1}{{\sqrt {pq}}^{3}}}\left(pq^{3}-qp^{3}\right)\\&={\frac {pq}{{\sqrt {pq}}^{3}}}(q-p)\\&={\frac {q-p}{\sqrt {pq}}}\end{aligned}}

Wölbung und Exzess Bearbeiten

Der Exzess der Bernoulli-Verteilung ist

\gamma (X)={\frac {1-6pq}{pq}}

und damit ist die Wölbung

\beta _{2}(X)={\frac {1-3pq}{pq}}

.

Momente Bearbeiten

Alle k-ten Momente $m_{k}$ sind gleich und es gilt

m_{k}=p

.

Es ist nämlich

m_{k}=\operatorname {E} \left(X^{k}\right)=p\cdot 1^{k}+q\cdot 0^{k}=p

.

Entropie Bearbeiten

Die Entropie der Bernoulli-Verteilung ist

\mathrm {H} =-q\log _{2}(q)-p\log _{2}(p)

gemessen in Bit.

Modus Bearbeiten

Der Modus der Bernoulli-Verteilung ist

x_{D}={\begin{cases}0&{\text{falls }}\quad q>p\\0;1&{\text{falls }}\quad q=p\\1&{\text{falls }}\quad q<p\end{cases}}

.

Median Bearbeiten

Der Median der Bernoulli-Verteilung ist

{\tilde {m}}_{X}={\begin{cases}0&{\text{falls }}\quad q>p,\\1&{\text{falls }}\quad q<p,\end{cases}}

falls $p=q$ gilt, ist jedes ${\tilde {m}}_{X}\in [0,1]$ ein Median.

Kumulanten Bearbeiten

Die kumulantenerzeugende Funktion ist

g_{X}(t)=\ln(pe^{t}+q)

.

Damit sind die ersten Kumulanten $\kappa _{1}=p,\kappa _{2}=pq$ und es gilt die Rekursionsgleichung

\kappa _{n+1}=p(1-p){\frac {d\kappa _{n}}{dp}}.

Wahrscheinlichkeitserzeugende Funktion Bearbeiten

Die wahrscheinlichkeitserzeugende Funktion ist

m_{X}(t)=1-p+pt

.

Charakteristische Funktion Bearbeiten

Die charakteristische Funktion ist

\varphi _{X}(t)=1-p+pe^{\mathrm {i} t}

.

Momenterzeugende Funktion Bearbeiten

Die momenterzeugende Funktion ist

M_{X}(t)=1-p+pe^{t}

.

Beziehung zu anderen Verteilungen Bearbeiten

Beziehung zur Binomialverteilung Bearbeiten

Die Bernoulli-Verteilung ist ein Spezialfall der Binomialverteilung für $n=1$ . Mit anderen Worten, die Summe von unabhängigen Bernoulli-verteilten Zufallsgrößen mit identischem Parameter $p$ genügt der Binomialverteilung, demnach ist die Bernoulli-Verteilung nicht reproduktiv. Die Binomialverteilung ist die $n$ -fache Faltung der Bernoulli-Verteilung bei gleichem Parameter $p$ bzw. mit gleicher Wahrscheinlichkeit $p$ .

Beziehung zur verallgemeinerten Binomialverteilung Bearbeiten

Die Summe von $n$ voneinander unabhängigen Bernoulli-verteilten Zufallsvariablen, die alle einen unterschiedlichen Parameter $p_{i}$ besitzen, ist verallgemeinert binomialverteilt.

Beziehung zur Poisson-Verteilung Bearbeiten

Die Summe von Bernoulli-verteilten Zufallsgrößen genügt für $n\to \infty$ , $p_{n}\to 0$ und $\lim \limits _{n\to \infty }np_{n}=\lambda >0$ einer Poisson-Verteilung mit dem Parameter $\lambda$ . Dies folgt direkt daraus, dass die Summe binomialverteilt ist und für die Binomialverteilung die Poisson-Approximation gilt.

Beziehung zur Zweipunktverteilung Bearbeiten

Die Bernoulli-Verteilung ist ein Spezialfall der Zweipunktverteilung mit $a=0,b=1$ . Umgekehrt ist die Zweipunktverteilung eine Verallgemeinerung der Bernoulli-Verteilung auf beliebige zweielementige Punktmengen.

Beziehung zur Rademacher-Verteilung Bearbeiten

Sowohl die Bernoulli-Verteilung mit $p=q=0{,}5$ als auch die Rademacher-Verteilung modellieren einen fairen Münzwurf (oder eine faire, zufällige Ja/Nein-Entscheidung). Der Unterschied besteht lediglich darin, dass Kopf (Erfolg) und Zahl (Misserfolg) unterschiedlich codiert werden.

Beziehung zur geometrischen Verteilung Bearbeiten

Bei Hintereinanderausführung von Bernoulli-verteilten Experimenten ist die Wartezeit auf den ersten Erfolg (oder letzten Misserfolg, je nach Definition) geometrisch verteilt.

Beziehung zur diskreten Gleichverteilung Bearbeiten

Die Bernoulli-Verteilung mit $p=q={\frac {1}{2}}$ ist eine diskrete Gleichverteilung auf $\{0,1\}$ .

Urnenmodell Bearbeiten

Die Bernoulli-Verteilung lässt sich auch aus dem Urnenmodell erzeugen, wenn $p={\frac {k}{n}}$ mit $k,n\in \mathbb {N}$ ist. Dann entspricht dies dem einmaligen Ziehen aus einer Urne mit $n$ Kugeln, von denen genau $k$ rot sind und alle anderen eine andere Farbe besitzen. Die Wahrscheinlichkeit, eine rote Kugel zu ziehen, ist dann $p$ .

Simulation Bearbeiten

Bei der Simulation macht man sich zunutze, dass, wenn ${\mathcal {U}}$ eine stetig gleichverteilte Zufallsvariable auf $[0,1]$ ist, die Zufallsvariable $Y=\mathbf {1} _{\{{\mathcal {U}}\geq 1-p\}}$ Bernoulli-verteilt ist mit Parameter $p$ . Da fast jeder Computer Standardzufallszahlen erzeugen kann, ist die Simulation wie folgend:

Erzeuge eine Standardzufallszahl $u_{i}$
Ist $u_{i}\leq 1-p$ , gib 0 aus, ansonsten gib 1 aus.

Dies entspricht genau der Inversionsmethode. Die einfache Simulierbarkeit von Bernoulli-verteilten Zufallsvariablen kann auch zur Simulation von binomialverteilten oder verallgemeinert Binomialverteilten Zufallsvariablen genutzt werden.

Literatur Bearbeiten

Hans-Otto Georgii: Stochastik: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4. Auflage, de Gruyter, 2009, ISBN 978-3-11-021526-7.

Einzelnachweise Bearbeiten

↑ ^a ^b P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, S. 527.
↑ Norbert Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. Eine Einführung. 2., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1, S. 63, doi:10.1007/978-3-642-45387-8.
↑ Klaus D. Schmidt: Maß und Wahrscheinlichkeit. 2., durchgesehene Auflage. Springer-Verlag, Heidelberg Dordrecht London New York 2011, ISBN 978-3-642-21025-9, S. 254, doi:10.1007/978-3-642-21026-6.
↑ James Victor Uspensky: Introduction to Mathematical Probability, McGraw-Hill, New York 1937, Seite 45

[Lex-527-1] P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, S. 527.

[2] Norbert Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. Eine Einführung. 2., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1, S. 63, doi:10.1007/978-3-642-45387-8.

[3] Klaus D. Schmidt: Maß und Wahrscheinlichkeit. 2., durchgesehene Auflage. Springer-Verlag, Heidelberg Dordrecht London New York 2011, ISBN 978-3-642-21025-9, S. 254, doi:10.1007/978-3-642-21026-6.

[4] James Victor Uspensky: Introduction to Mathematical Probability, McGraw-Hill, New York 1937, Seite 45

[1]

[2]

[3]

[4]