Ein Kegel oder Konus ist ein geometrischer Körper, der entsteht, wenn man alle Punkte eines in einer Ebene liegenden, begrenzten und zusammenhängenden Flächenstücks geradlinig mit einem Punkt außerhalb der Ebene verbindet. Ist das Flächenstück eine Kreisscheibe, wird der Körper Kreiskegel genannt. Das Flächenstück nennt man Grundfläche, deren Begrenzungslinie die Leitkurve, den Punkt nennt man Spitze, Apex oder Scheitel des Kegels und die Fläche an der Seite wird als Mantelfläche bezeichnet. Ein Kegel hat also eine Spitze (den Scheitelpunkt), eine Kante (die Leitkurve) und zwei Flächen (die Mantel- und die Grundfläche).
Die Spitze eines Kegels ist kein Eckpunkt, da es sich bei der Spitze nicht um einen Endpunkt von Kanten handelt (vgl. Definition von Ecke).
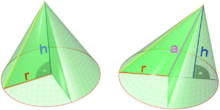
Unter der Höhe des Kegels versteht man sowohl das Lot von der Spitze auf die Grundfläche (die Höhe steht also immer senkrecht zur Grundfläche) wie auch die Länge dieses Lotes (also den Abstand der Spitze von der Grundfläche).
Die Verbindungsstrecken der Spitze mit der Leitkurve heißen Mantellinien, ihre Vereinigung bildet den Kegelmantel oder die Mantelfläche. Ellipse, Parabel und Hyperbel sind Kegelschnitte. Im Zusammenhang mit Kegelschnitten wird als „Kegel“ oft auch ein „Doppelkegel“ verstanden.
Vor allem in der Technik wird ein Kegel oder ein Kegelstumpf oft als Konus (von lat. conus) bzw. als konisch bezeichnet.
Gerader, schiefer und gleichseitiger Kegel Bearbeiten
Wenn in der Geometrie von einem Kegel gesprochen wird, ist häufig der Spezialfall des geraden Kreiskegels gemeint. Unter einem Kreiskegel versteht man einen Körper, der durch einen Kreis (Grundkreis oder Basiskreis) und einen Punkt außerhalb der Ebene des Kreises (Spitze des Kegels) festgelegt ist.
Die Ebene, in welcher der Basiskreis liegt, heißt Basis(kreis)ebene. Unter dem Radius des Kegels versteht man normalerweise den Radius des Basiskreises. Die Gerade durch den Mittelpunkt des Grundkreises und die Spitze nennt man die Achse des Kegels. Die Höhe des Kegels ist der Abstand der Spitze von der Basisebene; dieser Abstand muss senkrecht zur Basisebene gemessen werden.
Steht die Achse senkrecht zur Basisebene, so liegt ein gerader Kreiskegel oder Drehkegel vor. Andernfalls spricht man von einem schiefen Kreiskegel oder elliptischen Kegel. Jeder elliptische Kegel hat zwei Richtungen, in denen sein Schnitt mit einer Ebene ein Kreis ist; diese Tatsache macht sich die stereografische Projektion als Kreistreue zunutze.
Die Bezeichnung „Drehkegel“ deutet darauf hin, dass es sich um einen Rotationskörper handelt. Er entsteht durch Rotation eines rechtwinkligen Dreiecks um eine seiner beiden Katheten. In diesem Fall werden die Mantellinien (also die Verbindungsstrecken der (Rand-)Punkte des Basiskreises mit der Spitze) auch Erzeugende genannt ( ), da sie den Mantel „erzeugen“. Der Öffnungswinkel beträgt das Doppelte des Winkels zwischen den Mantellinien und der Achse eines Drehkegels. Der Winkel zwischen den Mantellinien und der Achse heißt halber Öffnungswinkel.
Ein Drehkegel mit Öffnungswinkel 60° heißt gleichseitiger Kegel, denn schneidet man ihn mit einer Ebene, die die Achse enthält, so erhält man ein gleichseitiges Dreieck.
Größen und Formeln Bearbeiten
| Größen und Formeln | ||
|---|---|---|
| Radius eines geraden Kreiskegels |
||
| Höhe eines geraden Kreiskegels |
||
| Mantellinie eines geraden Kreiskegels |
||
| Halber Öffnungswinkel eines geraden Kreiskegels |
||
| Durchmesser der Grundfläche eines geraden Kreiskegels |
||
| Grundfläche eines Kreiskegels |
||
| Flächeninhalt der Mantelfläche eines geraden Kreiskegels |
||
| Oberfläche eines geraden Kreiskegels |
||
| Volumen eines beliebigen Kreiskegels |
||
| Trägheitsmoment eines geraden Kreiskegels (Drehung um die Symmetrieachse) |
massiver Kegel: Kegelmantel:
| |
Beweise Bearbeiten
Volumen Bearbeiten
Bereits im Jahr 1781 beschreibt Johann Friedrich Lorenz in seiner Übersetzung Euklids Elemente Euklids Feststellung: Jeder Kegel ist der dritte Theil eines Cylinders, welcher mit ihm einerley Grundfläche, ABCD, und gleiche Höhe hat.[1] In der Elementargeometrie wird die Volumenformel oft mit dem Prinzip von Cavalieri begründet. Man vergleicht den gegebenen Kreiskegel mit einer Pyramide von gleicher Grundfläche und Höhe. Für Parallelebenen zur Grundfläche in beliebigem Abstand folgt aus den Gesetzen der Ähnlichkeit bzw. der zentrischen Streckung, dass die entsprechenden Schnittflächen gleichen Flächeninhalt besitzen. Daher müssen die beiden Körper im Volumen übereinstimmen. Die für Pyramiden der Grundfläche und Höhe gültige Volumenformel
kann daher auf den Kegel übertragen werden. Zusammen mit der Formel für die Kreisfläche erhält man
- .
Es ist auch möglich, den Kegel durch eine Pyramide mit regelmäßigem n-Eck als Grundfläche (für ) anzunähern.
Ein anderer Beweis (hier speziell für den geraden Kreiskegel dargestellt) setzt die Integralrechnung als Hilfsmittel ein. Es wird ein kartesisches Koordinatensystem verwendet, wobei die Kegelspitze im Ursprung (0|0) und der Mittelpunkt des Grundkreises im Punkt ( |0) liegen. Man kann sich nun den Kegel zusammengesetzt denken aus unendlich vielen zylindrischen Scheiben infinitesimaler (unendlich kleiner) Höhe (Dicke) . Da der Abstand einer solchen Zylinderscheibe von der Kegelspitze durch die Koordinate gegeben ist, gilt nach dem Strahlensatz:
- Radius eines infinitesimalen Zylinders:
- Volumen eines infinitesimalen Zylinders:
Das gesamte Volumen des Drehkegels entspricht der Gesamtheit all dieser unendlich kleinen Zylinder. Zur Berechnung bildet man das bestimmte Integral mit den Integrationsgrenzen 0 und :
Damit kommt man zur bekannten Formel
- .
Mantelfläche Bearbeiten
Die Mantelfläche eines geraden Kreiskegels ist gekrümmt, aber zu einem Kreissektor abwickelbar. Der Radius dieses Sektors stimmt mit der Länge einer Mantellinie des Kegels ( ) überein. Den Mittelpunktswinkel des Kreissektors kann man durch eine Verhältnisgleichung ermitteln. Er verhält sich zum 360°-Winkel wie die Kreisbogenlänge (Umfang des Basiskreises) zum gesamten Umfang eines Kreises mit Radius :
Der gesuchte Flächeninhalt der Mantelfläche ergibt sich nun aus der Formel für den Flächeninhalt eines Kreissektors:
Die Abwicklung der Mantelfläche eines geraden Kreiskegels wird in der Darstellenden Geometrie näherungsweise mit Zirkel und Lineal durchgeführt: s. Abwicklung (Darstellende Geometrie).
Mittelpunktswinkel Bearbeiten
Der Mittelpunktswinkel der Mantelfläche kann ausgehend von der Formel
berechnet werden:
Da für den halben Öffnungswinkel des Kegels ist, gilt:
- .
Doppelkegel Bearbeiten
Ein Doppelkegel bzw. Doppelkonus mit gegeneinander gerichteten Spitzen entsteht als Rotationsfläche einer Geraden um eine sie nicht rechtwinkelig schneidende Achse. Es entstehen zwei Drehkegel mit dem gleichen Öffnungswinkel und einer gemeinsamen Achse, die sich in der Spitze berühren. Schneidet man einen solchen unendlichen Doppelkegel mit einer Ebene, die die Spitze nicht enthält, so entstehen die (nicht ausgearteten) Kegelschnitte: Kreis, Ellipse, Parabel, Hyperbel.
Ein Doppelkegel mit auseinanderweisenden Spitzen entsteht, indem zwei gleiche Kegel mit ihrer Basis aneinandergefügt werden. Wird ein solcher Doppelkegel auf zwei in einem Winkel verlaufenden und leicht zum Schnittpunkt hin geneigten Geraden abgesetzt, so rollt dieser scheinbar aufwärts. Siehe: Aufwärtsrollender Doppelkegel
Wird ein gerader Kreiskegel, dessen Radius der Höhe entspricht, an der Grundfläche zu einem Doppelkegel gespiegelt und anschließend in einer Ebene geschnitten, die beide Spitzen enthält, so hat die Querschnittsfläche die Form eines Quadrats.
Wird eines dieser Quadrate um 90° rotiert und werden dann beide Hälften wieder zusammengefügt, erhält man ein Sphericon.
Analytische Beschreibung Bearbeiten
Ein senkrechter Kreiskegel (Doppelkegel) mit der Spitze im Ursprung und der z-Achse als Symmetrieachse lässt sich durch eine Gleichung
beschreiben. Die Zahl ist der Radius der Höhenkreise der Höhen . Ist , so vereinfacht sich die Gleichung zu
und man nennt in diesem Fall den Kegel Einheitskegel (analog zum Einheitskreis).
So, wie eine beliebige Ellipse das affine Bild des Einheitskreises ist, ist ein beliebiger Kegel (als Quadrik) das affine Bild des Einheitskegels. Die einfachsten affinen Abbildungen sind Skalierungen der Koordinaten. Skaliert man die x- und y-Achse, so ergeben sich Kegel mit Gleichungen
Die Höhenschnitte solcher Kegel sind Ellipsen. Der Schnitt mit der Höhenebene ist die Ellipse . Der Kegel ist gleich der Vereinigung aller Geraden (Erzeugenden) durch die Spitze und die Ellipsenpunkte. Beschreibt man die Ellipse durch die Parameterdarstellung und stellt die Erzeugenden in Parameterform dar, erhält man die folgende Parameterdarstellung des Kegels :
Die Gleichung eines im Raum beliebig gelagerten Kegels ist schwierig anzugeben. Die Parameterdarstellung eines beliebigen Kegels dagegen relativ einfach:
Dabei ist die Spitze des Kegels und sind drei linear unabhängige Vektoren. zeigt in Richtung der Kegelachse (s. Bild).[2] Für jeden konstanten Parameter ergibt sich eine Ellipse, mit der man sich (zusammen mit der Spitze) den Kegel erzeugt denken kann.
Sind die drei Vektoren paarweise orthogonal und ist , so wird durch die Parameterdarstellung ein senkrechter Kreiskegel beschrieben.
Dass ein beliebiger elliptischer Kegel auch immer Kreise enthält, wird in Kreisschnittebene gezeigt.
Verallgemeinerungen Bearbeiten
- Konvexe Mengen
Man verallgemeinert die Eigenschaft des (unendlichen) Kegels, aus Strahlen mit gemeinsamem Anfangspunkt zu bestehen, zu kegelförmigen Mengen, zu denen dann z. B. auch eine unendlich hohe Pyramide gehört. Besonderes Interesse gilt dabei den konvexen Kegeln, die in der linearen Optimierung eine Rolle spielen.
Dabei ist der Begriff des Ordnungskegels wichtig: Definiert man eine Halbordnung mittels , wobei ein konvexer und abgeschlossener Kegel ist, so ist diese reflexiv, antisymmetrisch, transitiv und multiplikativ sowie additiv verträglich. Damit ist eine solche Halbordnung eine Verallgemeinerung der (komponentenweisen) arithmetischen Halbordnung, der der positive Orthant zugrunde liegt. Eine mögliche Definition eines solchen Kegels lautet:
Sei ein reeller Banachraum und eine nichtleere Teilmenge von . heißt Kegel, wenn folgende Bedingungen erfüllt sind:
- ist abgeschlossen,
- ,
- ,
- .
Wird die vierte Bedingung weggelassen, so erhält man eine mögliche Definition eines Keils.
Allgemeinere Grundflächen
- Als weitere Verallgemeinerung des Kegels kann man beliebige Grundflächen zulassen. Der Kegel entsteht dann als konvexe Hülle der Grundfläche und eines weiteren Punktes außerhalb der Fläche (der Kegelspitze). In diesem Sinne ist eine Pyramide ein Kegel über einem Vieleck.
- In der synthetischen Geometrie wird der Begriff Kegel für bestimmte quadratische Mengen in projektiven Geometrien beliebiger Dimension definiert. Siehe dazu Quadratische Menge#Kegel.
- Topologie
In der Topologie versteht man unter dem Kegel über einem topologischen Raum den Raum, den man aus dem Produkt durch Identifikation aller Punkte in (der „Kegelspitze“) erhält.
Den entsprechenden „Doppelkegel“ (durch zusätzliche Identifikation von ) bezeichnet man auch als Einhängung oder Suspension.
Anwendungsbeispiele Bearbeiten
Trinkglas Bearbeiten
Einige Trinkgläser, zum Beispiel ein Martiniglas, haben annähernd die Form eines Kegels.
Ein Martiniglas mit dem Durchmesser 103 Millimeter und der Füllhöhe 59 Millimeter wird bis zum Rand mit Orangensaft gefüllt. Daraus ergeben sich das Volumen und die Mantelfläche:
- Volumen:
- Mantelfläche:
Das Martiniglas kann also mit etwa 164 Millilitern Orangensaft gefüllt werden. Die äußere Oberfläche beträgt etwa 127 Quadratzentimeter.
Weitere Beispiele Bearbeiten
-
Glastrichter mit eingelegtem Rundfilter
-
Apollo-Dockingsystem
Siehe auch Bearbeiten
Literatur Bearbeiten
- Rolf Baumann: Geometrie für die 9./10. Klasse. Zentrische Streckung, Satz des Pythagoras, Kreis- und Körperberechnungen. 4. Auflage. Mentor-Verlag, München 2003, ISBN 3-580-63635-9.
Weblinks Bearbeiten
- Das Namensgeheimnis der Kegelschnitte. In: Johanneum-Lueneburg.de
Einzelnachweise Bearbeiten
- ↑ Johann Friedrich Lorenz: Euklids Elemente, fünfzehn Bücher, aus dem Griechischen übersetzt. Hrsg.: Im Verlag der Buchhandlung des Waysenhauses. Zwölftes Buch. Halle 1781, S. 308 ff. (Der 10. Satz. Jeder Kegel ist der dritte Theil eines Cylinders, … [abgerufen am 1. November 2018]).
- ↑ E. Hartmann: Computerunterstützte Darstellende und konstruktive Geometrie. Uni Darmstadt (PDF; 3,4 MB), S. 105.