Paraboloid
Ein Paraboloid ist eine Fläche zweiter Ordnung (Quadrik) und wird in den einfachsten Fällen durch eine Gleichung beschrieben:
- für elliptisches Paraboloid
- für ein hyperbolisches Paraboloid
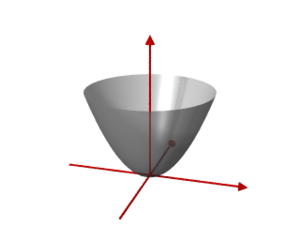
Elliptische Paraboloide begegnen einem beispielsweise als Oberflächen von Satellitenschüsseln und als Energieentwertungsdiagramme[1] beim Stoß rauer Starrkörper.
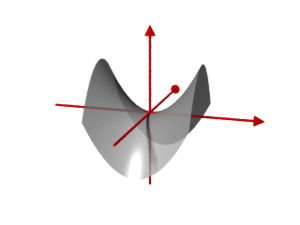
Hyperbolische Paraboloide sind Sattelflächen. Sie enthalten Geraden und werden deswegen von Architekten und Bauingenieuren als leicht modellierbare Dachformen (hyperbolische Paraboloidschalen) verwendet[2].
Anhand der Gleichungen erkennt man, dass beide Flächen viele Parabeln enthalten, was zur Namensgebung beigetragen hat:
ist eine Rotationsfläche. entsteht durch Rotation der Parabel in der x-z-Ebene mit der Gleichung um die z-Achse.
ist keine Rotationsfläche. Aber auch bei ist bis auf zwei Ausnahmen jeder Schnitt mit einer Ebene durch die z-Achse eine Parabel. Z. B. ist der Schnitt mit der Ebene (y-z-Ebene) die Parabel .
Beide Flächen lassen sich als Schiebflächen auffassen und lassen sich durch verschieben einer Parabel entlang einer zweiten Parabel erzeugen.
Allerdings gibt es auch wesentliche Unterschiede:
- besitzt als Höhenschnitte Kreise (für konstantes ). Im allgemeinen Fall sind es Ellipsen (siehe unten), was sich im Namenszusatz widerspiegelt,
- besitzt als Höhenschnitte Hyperbeln oder Geraden (für ), was den Zusatz hyperbolisch rechtfertigt.
Ein hyperbolisches Paraboloid ist nicht mit einem Hyperboloid zu verwechseln.
Eigenschaften Bearbeiten
Elliptisches Paraboloid Bearbeiten
Das elliptische Paraboloid ergibt sich durch Rotation des Graphen der Funktion um die -Achse. Für die Ableitung gilt . Das Volumen und die Oberfläche für ein elliptische Paraboloid mit der Höhe ergeben sich nach den Guldinschen Regeln mithilfe von Integralen.
Volumen Bearbeiten
Oberfläche Bearbeiten
Tangentialebenen Bearbeiten
Die Tangentialebene in einem Flächenpunkt an den Graphen einer differenzierbaren Funktion hat die Gleichung
- .
Für ergibt sich für die Gleichung der Tangentialebene im Punkt
- .
Ebene Schnitte Bearbeiten
Das elliptische Paraboloid ist eine Rotationsfläche und entsteht durch Rotation der Parabel um die -Achse. Ein ebener Schnitt von ist:
- eine Parabel, falls die Ebene senkrecht (parallel zur -Achse) ist.
- eine Ellipse oder ein Punkt oder leer, falls die Ebene nicht senkrecht ist. Eine horizontale Ebene schneidet in einem Kreis.
- ein Punkt, falls die Ebene eine Tangentialebene ist.
Affine Bilder Bearbeiten
Ein beliebiges elliptisches Paraboloid ist ein affines Bild von . Die einfachsten affinen Abbildungen sind Skalierungen der Koordinatenachsen. Sie liefern die Paraboloide mit den Gleichungen
- .
besitzt immer noch die Eigenschaft, dass es von einer senkrechten Ebene in einer Parabel geschnitten wird. Eine horizontale Ebene schneidet allerdings hier in einer Ellipse, falls gilt. Dass ein beliebiges elliptisches Paraboloid auch immer Kreise enthält, wird in Kreisschnittebene gezeigt.
ist
- symmetrisch zu den - bzw. -Koordinatenebenen.
- symmetrisch zur -Achse, d. h. lässt invariant.
- rotationssymmetrisch, falls ist.
Bemerkung:
- Ein Rotationsparaboloid (d. h. ) hat als Parabolspiegel große technische Bedeutung, da alle Parabeln mit der Rotationsachse als Achse denselben Brennpunkt besitzen.
- Wenn man ein mit Wasser gefülltes Glas mit konstanter Drehgeschwindigkeit um seine Symmetrieachse rotieren lässt, dreht sich das Wasser nach einer Weile mit dem Glas mit. Seine Oberfläche bildet dann ein Rotationsparaboloid.
- Ein elliptisches Paraboloid wird oft kurz Paraboloid genannt.
Homogene Koordinaten Bearbeiten
Führt man homogene Koordinaten so ein, dass die Fernebene durch die Gleichung beschrieben wird, muss man setzen. Nach Beseitigung des Nenners erhält man die homogene Beschreibung von durch die Gleichung:
- .
Der Schnitt des Paraboloids mit der Fernebene ist der Punkt .
Die Koordinatentransformation liefert die Gleichung
- .
In den neuen Koordinaten schneidet die Ebene das Paraboloid nicht.
Führt man jetzt wieder affine Koordinaten durch ein, erhält man die Gleichung der Einheitskugel:
Dies zeigt: Ein elliptisches Paraboloid ist projektiv äquivalent zu einer Kugel.
Hyperbolisches Paraboloid Bearbeiten
Tangentialebenen Bearbeiten
Für ist die Gleichung der Tangentialebene (siehe oben) im Punkt
- .
Ebene Schnitte Bearbeiten
ist im Gegensatz zu keine Rotationsfläche. Aber wie bei sind bei auch fast alle senkrechten ebenen Schnitte Parabeln:
Der Schnitt einer Ebene mit ist
- eine Parabel, falls die Ebene senkrecht (parallel zur -Achse) ist und eine Gleichung hat.
- eine Gerade, falls die Ebene senkrecht ist und eine Gleichung hat.
- ein sich schneidendes Geradenpaar, falls die Ebene eine Tangentialebene ist (siehe Abbildung).
- eine Hyperbel, falls die Ebene nicht senkrecht und keine Tangentialebene ist (siehe Abbildung).
Weitere Eigenschaften Bearbeiten
- Die Schnittparabeln mit Ebenen parallel zur - oder -Ebene sind alle kongruent zur Normparabel .
- ist eine Schiebfläche. entsteht durch Verschiebung der Parabel mit ihrem Scheitel entlang der Parabel .
- Eine nicht senkrechte Ebene, die eine Gerade enthält, enthält immer auch eine zweite Gerade und ist eine Tangentialebene.
- Da die Fläche Geraden enthält, ist sie eine Regelfläche.
- ist ein Konoid.
- Ein hyperbolisches Paraboloid enthält zwar Geraden (ebenso wie Zylinder und Kegel), ist aber nicht abwickelbar, da die Gaußsche Krümmung in jedem Punkt ungleich 0 ist. Die Gaußsche Krümmung ist überall kleiner als 0. Bei einer Kugel ist die Gaußsche Krümmung überall größer als 0. Damit ist ein hyperbolisches Paraboloid eine Sattelfläche.
- Durch eine Drehung des Koordinatensystems um die -Achse um 45 Grad geht die Gleichung in die einfachere Gleichung über.
Affine Bilder Bearbeiten
Ein beliebiges hyperbolisches Paraboloid ist ein affines Bild von . Die einfachsten affinen Abbildungen sind Skalierungen der Koordinatenachsen. Sie liefern die hyperbolischen Paraboloide mit den Gleichungen
- .
ist
- symmetrisch zu den - bzw. -Koordinatenebenen.
- symmetrisch zur -Achse, d. h. lässt invariant.
Bemerkung:
Hyperbolische Paraboloide werden von Architekten zur Konstruktion von Dächern verwendet (siehe Abbildung), da sie leicht mit Geraden (Balken) modelliert werden können.
Interpolationsfläche von 4 Punkten Bearbeiten
Ein hyperbolisches Paraboloid lässt sich auch als bilineare Interpolationsfläche von vier nicht in einer Ebene liegenden Punkten auffassen[3]:
- .
Das Netz der Parameterlinien besteht aus Geraden.
Für das in der Abbildung dargestellte Beispiel ist . Das dadurch beschriebene hyperbolische Paraboloid hat die Gleichung .
Siehe hierzu auch die Darstellung in baryzentrischen Koordinaten.
Homogene Koordinaten Bearbeiten
Führt man wie bei homogene Koordinaten ein, erhält man die Beschreibung des hyperbolischen Paraboloids durch die Gleichung:
- .
Der Schnitt des Paraboloids mit der Fernebene besteht aus den beiden Geraden , die sich in dem Punkt schneiden.
Die Koordinatentransformation liefert die Gleichung
- .
Die Fernebene schneidet das Paraboloid in einem Kreis.
Geht man wieder zu affinen Koordinaten über, erhält man die Gleichung
eines einschaligen Hyperboloids.
Das hyperbolische Paraboloid ist also projektiv äquivalent zu einem einschaligen Hyperboloid.
Grenzfläche zwischen Scharen von elliptischen und hyperbolischen Paraboloiden Bearbeiten
Lässt man in den Gleichungen
- (Schar von elliptischen Paraboloiden)
und
- (Schar von hyperbolischen Paraboloiden)
den Parameter gegen laufen, so erhält man die Gleichung der gemeinsamen Grenzfläche
- .
Dies ist die Gleichung eines parabolischen Zylinders mit einer Parabel als Querschnitt (siehe Abbildung).
Anwendungen Bearbeiten
Beispiele aus dem täglichen Leben sind Reflektoren von Scheinwerfern, Parabolantennen und Parabolspiegel in der Astronomie.
Wenn man eine Flüssigkeit gleichmäßig um eine senkrechte Achse dreht, überlagern sich Schwerkraft und Fliehkraft, und die Flüssigkeitsoberfläche nimmt die Form eines Rotationsparaboloids an. So funktioniert das Quecksilber-Teleskop. Auf diese Weise kann man auch Parabolspiegel für Spiegelteleskope gießen, um danach nicht so viel Material abschleifen zu müssen, da die beim Guss erhaltene Oberfläche bereits ein Rotationsparaboloid darstellt.
Siehe auch Bearbeiten
Einzelnachweise Bearbeiten
- ↑ K.-E. Kurrer: Zur Darstellung der Energietransformation beim ebenen gekoppelten Reibungsstoß mit Hilfe des Energieentwertungsdiagramms. In: Cassius Alexandru, Günter Gödert, Uwe Görn, Roland Parchem und Joachim Villwock (Hrsg.): Beiträge zur Mechanik. Festschrift zum 65. Geburtstag von Prof. Dr. Rudolf Trostel. Universitätsbibliothek der TU Berlin, Abt. Publikation, Berlin 1993, ISBN 3-7983-1581-7, S. 148–169.
- ↑ K.-E. Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin 2018, S. 743–747, ISBN 978-3-433-03229-9
- ↑ G. Farin: Curves and Surfaces for Computer Aided Geometric Design, Academic Press, 1990, ISBN 0-12-249051-7, S. 250








