Benutzer:Googolplexian1221/Reihe (Mathematik)

Die Reihe ${\tfrac {1}{2}}+{\tfrac {1}{4}}+{\tfrac {1}{8}}+\cdots$ konvergiert gegen 1

Eine Reihe, selten Summenfolge oder unendliche Summe, und vor allem in älteren Darstellungen auch unendliche Reihe genannt, ist ein Objekt aus dem mathematischen Teilgebiet der Analysis. Anschaulich ist eine Reihe eine Summe mit unendlich vielen Summanden, wie etwa

${\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+{\frac {1}{32}}+\cdots .$

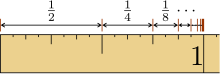
Man kann Reihen als rein formale Objekte studieren, jedoch sind Mathematiker in vielen Fällen an der Frage interessiert, ob eine Reihe konvergiert, sich die unendlich lange Summe also langfristig einem festen Wert immer weiter annähert. In etwa konvergiert die obere Beispielreihe gegen den Wert $1$ (siehe Bild). Allgemein wird eine Reihe $a_{0}+a_{1}+a_{2}+\cdots$ mit $\textstyle \sum _{n=0}^{\infty }a_{n}$ bezeichnet, und dies ist, falls existent, gleichzeitig die Bezeichnung für den Grenzwert.

Präzise wird eine Reihe als eine Folge definiert, deren Glieder die Partialsummen einer anderen Folge sind. Wenn man die Zahl 0 zur Indexmenge zählt, ist die $n$-te Partialsumme die Summe der ersten $n+1$ (von den unendlich vielen) Summanden. Falls die Folge dieser Partialsummen einen Grenzwert besitzt, so wird dieser der Wert oder die Summe der Reihe genannt.

Einführung: Unendliche Summierbarkeit und erste Beispiele

Unter einer Reihe versteht man, veranschaulicht, eine niemals endende Summe von Zahlen. Dies können reelle, aber auch komplexe Zahlen sein. Die Dezimalschreibweise einer reellen Zahl kann als Reihe aufgefasst werden, etwa

${\frac {1}{3}}=0{,}333333\ldots =0{,}3+0{,}03+0{,}003+0{,}0003+0{,}00003+0{,}000003+\cdots$

oder auch

$\pi =3{,}14159\ldots =3+0{,}1+0{,}04+0{,}001+0{,}0005+0{,}00009+\cdots$

mit der Kreiszahl $\pi$. Die durch die Punkte angedeuteten Summen enden niemals, da die Dezimalentwicklung von ${\tfrac {1}{3}}$ periodisch und die Kreiszahl irrational ist. Es gibt Reihen, denen kein Wert zugeordnet werden kann, etwa

$1+2+3+4+\cdots$

aber auch solche, die gegen einen Grenzwert konvergieren (wie die oberen Beispiele mit Grenzwerten ${\tfrac {1}{3}}$ bzw. $\pi$).

Definition und Grundlagen

Für reelle und komplexe Folgen

Ist eine beliebige reelle (oder komplexe) Folge $\left(a_{j}\right)_{j\in \mathbb {N} _{0}}$ gegeben, kann man aus ihr eine neue Folge $\left(s_{n}\right)_{n\in \mathbb {N} _{0}}$ der Partialsummen bilden. Die $n$-te Partialsumme ist die Summe der ersten $n+1$ Glieder von $\left(a_{j}\right)_{j\in \mathbb {N} _{0}}$, ihre Definition lautet:

$s_{n}:=a_{0}+a_{1}+\dotsb +a_{n}.$

Die Folge $\left(s_{n}\right)_{n\in \mathbb {N} _{0}}$ der $n$-ten Partialsummen heißt Reihe.

Zu bemerken ist, dass aus der Definition folgt, dass andersherum jede Zahlenfolge $a_{0},a_{1},a_{2},a_{3},\dots$ zu einer Reihe wird, wenn man diese als Partialsummen der Folge $a_{0},(a_{1}-a_{0}),(a_{2}-a_{1}),(a_{3}-a_{2}),\dots$ auffasst. Eine Reihe ist also nichts anderes als eine Folge spezieller „Bauart“, deren Glieder rekursiv durch $s_{0}:=a_{0}$ und $s_{n+1}:=s_{n}+a_{n+1}$ definiert sind. Allerdings führt die einfache rekursive Struktur der Reihen zu vergleichsweise sehr handlichen Konvergenzkriterien, siehe unten.

Konvergenz

Obwohl Reihen auch als formale Objekte studiert werden können, also „ohne Wert“, sind in der Mathematik die Fälle von besonderem Interesse, in welchem sich die Reihe langfristig einem ganz bestimmten Wert annähert. Falls die Reihe $\textstyle \sum _{k=0}^{\infty }a_{k}$, also die Folge der Partialsummen

$s_{0}=a_{0}$

$s_{1}=a_{0}+a_{1}$

$s_{2}=a_{0}+a_{1}+a_{2}$

$\vdots$

$s_{n}=\sum _{k=0}^{n}a_{k},\ldots$

konvergiert, so nennt man ihren Grenzwert

$\lim _{n\to \infty }s_{n}=\lim _{n\to \infty }\sum _{k=0}^{n}a_{k}$

den Wert der Reihe oder die Summe der Reihe. Dieser ist eindeutig bestimmt und wird meistens als $\textstyle \sum _{k=0}^{\infty }a_{k}$ notiert.

Bildliche Veranschaulichung des Konvergenzprinzips. Um den Grenzwert lassen sich beliebig dünne „Schläuche“ mit Breite $\varepsilon >0$ legen, und in jedem noch so dünen Schlauch liegen fast alle Folgeglieder.

Anschaulich bedeutet Konvergenz, dass sich eine Folge auf Dauer einer reellen oder komplexen Zahl beleibig nah annähert. Da der Umgang mit „dem Unendlichen“ zunächst nicht sinnvoll ist, umgeht man diese Schwierigkeit, indem man den Konvergenzbegriff mit endlichen Mitteln erklärt. Die Reihe $\textstyle \sum _{k=0}^{\infty }a_{k}$ nennt man dann konvergent gegen den Grenzwert $S$, wenn es zu jeder noch so kleinen Zahl $\varepsilon >0$ einen Index $N(\varepsilon )$ gibt, so dass für alle noch größeren Indizes $N>N(\varepsilon )$

$\left|a_{0}+a_{1}+a_{2}+\cdots +a_{N}-S\right|<\varepsilon$

erfüllt ist. Hat eine Reihe $a_{0}+a_{1}+a_{2}+a_{3}+\cdots$ etwa den Grenzwert $1$, so besagt die Wahl $\varepsilon =0,01$, dass alle bis auf endlich viele Partialsummen

$a_{0}+a_{1}+\cdots +a_{N}$

zwischen $0,99$ und $1,01$ liegen. Ebenso lässt sich mit $\varepsilon =0,0001$ - ab einem gewissen Index liegen also alle Partialsummen zwischen $0,9999$ und $1,0001$ - usw., verfahren. In den meisten Fällen ist dieses Kriterium für Konvergenz jedoch nicht brauchbar, da bereits ein Grenzwert $S$ bekannt sein muss, um es überhaupt anwenden zu können. Es ist im Allgemeinen jedoch überaus schwierig, den Grenzwert einer konvergenten Reihe annzugeben. Dies kann aber leicht umgangen werden, denn es kann gezeigt werden, dass eine Reihe genau dann konvergiert, wenn es für jede Zahl $\varepsilon >0$ einen Index $N(\varepsilon )$ gibt, so dass für alle größeren Indizes $M\geq N>N(\varepsilon )$ bereits

$|a_{N}+a_{N+1}+\cdots +a_{M-1}+a_{M}|<\varepsilon$

gilt. Man bezeichnet dies als das Cauchy-Kriterium, und es kommt ohne Verwendung eines expliziten Grenzwertes aus.

Bedingte und absolute Konvergenz

Es gibt unterschiedliche Arten der Konvergenz. Dies betrifft nicht die Konvergenzdefinition, die stets die selbe ist, sondern die „Güte“ der Konvergenz. So kann man zwei Typen konvergenter Reihen angeben: Jene, die gewissermaßen „stabil“ konvergieren, und solche, bei denen größere Vorsicht geboten ist, etwa bei der Umordnung von Summanden.

Konvergenzschema einer alterniernden Reihe, also mit wechselnden Vorzeichen gekoppelt mit monoton gegen Null fallenden Summanden.

Eine Reihe $\textstyle \sum _{k=0}^{\infty }a_{k}$ heißt absolut konvergent, wenn auch die zugehörige Reihe der Absolutbeträge $\textstyle \sum _{k=0}^{\infty }|a_{k}|$ konvergiert. Durch das Nehmen der Beträge vergisst man alle möglichen Vorzeichen bzw. Ausrichtungen der $a_{k}$, was Konvergenz erschwert, da dann kein Wegkürzen mehr möglich ist. Etwa ist die alternierende Reihe

$1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

konvergent, nicht aber

$1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots .$

Es ist $1-{\tfrac {1}{2}}+{\tfrac {1}{3}}-{\tfrac {1}{4}}+\cdots$ ein erstes Beispiel einer bedingt konvergenten Reihe, also eine, die nicht absolut konvergiert. Aus mathematischer Sicht ist absolute Konvergenz ein Vorteil, da dies das Rechnen mit Reihen vereinfacht. Etwa ist es im Falle bedingter Konvergenz nicht ohne Weiteres erlaubt, die Reihenfolge der Summanden zu ändern, ohne dabei möglicherweise den Grenzwert zu verändern. Damit entfällt bei bedingt konvergenten Reihen das noch für endliche Summen gültige Kommutativgesetz.

Überblick zu den Anwendungen

Das Konzept der Reihe spielt disziplinübergreifend eine zentrale Rolle in der Mathematik. Hauptanwendungsgebiet ist zunächst die Analysis, jedoch auch alle durch diese Sparte beeinflussten Bereiche, nicht zuletzt angewandte Gebiete wie die Ingenieurswissenschaften. Dabei entfalten Reihen ihre Nützlichkeit zum Beispiel dann, wenn es darum geht, bestimmte Funktionen annähernd auszurechnen, die für Anwendungen zwar nützlich aber dennoch kompliziert sind. Ein Beispiel sind die Winkelfunktionen, etwa der Sinus. Es gibt kein einfaches, „geschlossenes“ Verfahren, für Eingabewerte $x$ den Ausgabewert $\sin(x)$ zu berechnen, aber mittels Reihen können gute Näherungswerte relativ schnell berechnet werden, die in der Praxis ausreichen. Es gilt die Reihenentwicklung

$\sin(x)={\frac {x}{1}}-{\frac {x^{3}}{1\cdot 2\cdot 3}}+{\frac {x^{5}}{1\cdot 2\cdot 3\cdot 4\cdot 5}}-{\frac {x^{7}}{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7}}+\cdots =x-{\frac {x^{3}}{6}}+{\frac {x^{5}}{120}}-{\frac {x^{7}}{5040}}+\cdots ,$

kurz:

$\sin(x)=\sum _{k=0}^{\infty }(-1)^{k}{\frac {x^{2k+1}}{(2k+1)!}}.$

Etwa ist $\sin(1)=0{,}84147098\ldots$, und wegen $1^{2k+1}=1$ für alle $k$, als Näherung bis zum $x^{7}$-Term

$1-{\frac {1}{6}}+{\frac {1}{120}}-{\frac {1}{5040}}\approx 0{,}8414682.$

Notationshinweise

Für Reihen gibt es je nach Kontext unterschiedliche Notationen. In diesem Artikel werden als Indizes für die Glieder von Folge und Reihe die natürlichen Zahlen einschließlich der Null verwendet. Bei manchen Anwendungen ist es zweckmäßig, die Summation erst beim Index 1, 2 oder höher zu beginnen, selten kommen auch negative Indizes vor (siehe Laurent-Reihe). Mit Hilfe des Summenzeichens können die einzelnen Glieder der Reihe auch abgekürzt als

$s_{n}=\sum _{j=0}^{n}a_{j}$

geschrieben werden. Ebenso geht man bei der Folge der Einzelglieder vor und schreibt kurz

$S=\sum _{j=0}^{\infty }a_{j}.$

Gelegentlich werden ein Teil oder alle Indizes weggelassen, wenn Missverständnisse ausgeschlossen sind. Ist etwa wie hier im Kontext von Berechnungen mit unendlichen Reihen klar, dass generell bei 0 zu nummerieren angefangen wird, so steht

$S=\sum a_{j}$ für $S=\sum _{j=0}^{\infty }a_{j}.$

Semantik

Dem Symbol

$\sum _{j=0}^{\infty }a_{j}$

kommen zwei unterschiedliche Bedeutungen zu, zwischen denen aus dem Kontext heraus entschieden werden muss. Einmal steht das Symbol für den Wert der Reihe, der im Fall konvergenter Reihen existiert oder im Fall divergenter Reihen nicht existiert:

$\sum _{j=0}^{\infty }a_{j}=\lim _{N\to \infty }\sum _{i=0}^{N}a_{j}$.

Andererseits repräsentiert das Symbol die Reihe als Folge der Partialsummen, unabhängig vom Konvergenzverhalten:

$\sum _{j=0}^{\infty }a_{j}=(a_{0},a_{0}+a_{1},a_{0}+a_{1}+a_{2},a_{0}+a_{1}+a_{2}+a_{3},...)$.

Fast immer ist mit dem Symbol der Grenzwert gemeint. Wenn man die Folge der Partialsummen meinen möchte, benutzt man Wendungen wie „…die Reihe, betrachtet als Folge ihrer Partialsummen,…“

Begriff

Eine Reihe, selten Summenfolge oder unendliche Summe und vor allem in älteren Darstellungen auch unendliche Reihe genannt, ist ein Objekt aus dem mathematischen Teilgebiet der Analysis.

Geschichte

Anfänge im 17. Jahrhundert

Die Kurve hat die selbe Länge wie das entsprechende gerade Segment.

Reihen wurden in der Mathematik hauptsächlich eingeführt, um geometrische Probleme zu lösen. Ihre zunächst eher sporadische Verwendung gewann um 1650 an Bedeutung und war zum Beispiel entscheidend für die Entstehung der Infinitesimalrechnung. Besonders zu Zeiten von Isaac Newton und Gottfried Wilhelm Leibniz wurden viele Ergebnisse erzielt, und ein großer Teil des frühen Wissens um die Reihen geht auf sie zurück.

Obwohl Reihen schon früher gelegentlich vorkamen, wurden sie in der Mathematik erst ab dem 17. Jahrhundert wirklich bedeutsam. Ihre Verwendung erfolgte vor allem im Zusammenhang mit dem Problem der Quadratur und der Abmessung von Kurven durch Einteilung in lineare Segmente (siehe auch Rektifizierbarkeit). Im 17. Jahrhundert versuchten die Mathematiker, neue Methoden für die Quadratur gekrümmter Linien zu finden, die die Schwierigkeiten der so genannten Exhaustionsmethode vermeiden.

Rechnen mit Reihen

Im Gegensatz zu gewöhnlichen (endlichen) Summen gelten für Reihen einige übliche Regeln der Addition nur bedingt. Man kann also nicht bzw. nur unter bestimmten Voraussetzungen mit ihnen wie mit endlichen Summenausdrücken rechnen. Es stellen sich grundsätzlich die Fragen:

• Wie kann man Reihen addieren, und wie wirkt sich das auf Konvergenz und Grenzwerte aus?
• Wie kann man Reihen multiplizieren, und wie wirkt sich das auf Konvergenz und Grenzwerte aus?

Summen und Vielfache

Man kann konvergente Reihen gliedweise addieren, subtrahieren oder mit einem festen Faktor (aber nicht einer anderen Reihe) multiplizieren (vervielfachen). Die resultierenden Reihen sind ebenfalls konvergent, und ihr Grenzwert ist die Summe bzw. Differenz der Grenzwerte der Ausgangsreihen bzw. das Vielfache des Grenzwertes der Ausgangsreihe. D. h.

$\sum _{j=0}^{\infty }(a_{j}\pm b_{j})=\sum _{j=0}^{\infty }a_{j}\pm \sum _{j=0}^{\infty }b_{j}=s\pm t$

$\sum _{j=0}^{\infty }Aa_{j}=A\sum _{j=0}^{\infty }a_{j}=As$,

wenn $\textstyle \sum _{j=0}^{\infty }a_{j}=s$ und $\textstyle \sum _{j=0}^{\infty }b_{j}=t$.

Produkte

Man kann absolut konvergente Reihen gliedweise miteinander multiplizieren. Die Produktreihe ist ebenfalls absolut konvergent und ihr Grenzwert ist das Produkt der Grenzwerte der Ausgangsreihen. D. h.

$\sum _{j,k=0}^{\infty }(a_{j}b_{k})=\left(\sum _{j=0}^{\infty }a_{j}\right)\cdot \left(\sum _{k=0}^{\infty }b_{k}\right)$

Da die Schreibweise (auf der linken Seite der Gleichung) der Produktreihe mit zwei Indizes in bestimmten Zusammenhängen „unhandlich“ ist, wird die Produktreihe auch in Form des Cauchyprodukts geschrieben. Der Name ergibt sich daraus, dass die Glieder der Produktreihe mit Hilfe des cauchyschen Diagonalverfahrens gebildet werden, dabei werden die Glieder der Ausgangsfolgen in einem quadratischen Schema paarweise angeordnet, und die (durchnummerierten) Diagonalen dieses Schemas bilden die Produktglieder. Für die Produktreihe braucht man dann nur noch einen einzelnen Index. Die Produktreihe hat dann die folgende Form:

$\sum _{j,k=0}^{\infty }(a_{j}b_{k})=\sum _{n=0}^{\infty }(a_{0}\cdot b_{n}+a_{1}\cdot b_{n-1}+\dotsb +a_{n-1}\cdot b_{1}+a_{n}\cdot b_{0})=\sum _{n=0}^{\infty }\left(\sum _{m=0}^{n}a_{m}b_{n-m}\right)$

Rechnen innerhalb der Reihe

Klammerung (Assoziativität)

Man kann innerhalb einer konvergenten Reihe die Glieder beliebig durch Klammern zusammenfassen. Man kann also beliebig viele Klammern in den „unendlichen Summenausdruck“ einfügen, man darf sie nur nicht innerhalb eines (aus mehreren Termen zusammengesetzten) Gliedes setzen. Der Wert der Reihe ändert sich durch die zusätzlich eingefügte Klammerung dann nicht.

Dies gilt für divergente Reihen im Allgemeinen nicht, was man leicht am folgenden Beispiel erkennt: Die Reihe

$\sum _{j=0}^{\infty }(-1)^{j}=1-1+1-1+\dotsb$

divergiert, während die beklammerte Reihe

$\sum _{j=0}^{\infty }((-1)^{2j}+(-1)^{2j+1})=(1-1)+(1-1)+\dotsb =0+0+\dotsb =0$

gegen Null konvergiert und die anders beklammerte Reihe

$1+\sum _{j=1}^{\infty }((-1)^{2j-1}+(-1)^{2j})=1+(-1+1)+(-1+1)+\dotsb =1+0+0+\dotsb =1$

gegen noch eine andere Zahl konvergiert.

Andererseits kann man aber keine Klammern ohne Weiteres weglassen. Man kann das aber immer dann, wenn die resultierende Reihe wieder konvergent ist. In diesem Falle bleibt auch der Reihenwert unverändert: Sind die Glieder $A_{k}$ einer konvergenten Reihe $\textstyle \sum _{k=0}^{\infty }A_{k}$ selbst in Summenform $A_{k}=a_{\nu _{k}+1}+\cdots +a_{\nu _{k+1}}$ (mit $k=0,1,...$ und $\nu _{0}=-1$), so „darf“ man die sie umschließenden Klammern genau dann weglassen, wenn die dadurch entstehende neue Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ wieder konvergiert.

Umordnung (Kommutativität)

→ Hauptartikel: Umordnung von Reihen

Eine Umordnung einer Reihe wird durch eine Permutation ihrer Indexmenge dargestellt. Ist die Indexmenge zum Beispiel die Menge $\mathbb {N} _{0}$ der natürlichen Zahlen mit Null und $\sigma \colon \mathbb {N} _{0}\rightarrow \mathbb {N} _{0},\ k\mapsto \sigma (k)$, eine bijektive Abbildung der natürlichen Zahlen auf sich, so heißt

$\sum _{k=0}^{\infty }a_{\sigma (k)}$

eine Umordnung der Reihe

$\sum _{k=0}^{\infty }a_{k}.$

Man kann konvergente Reihen unter Beibehaltung ihres Wertes dann und nur dann beliebig umordnen, wenn sie unbedingt bzw. absolut konvergent sind. Es gilt für unbedingt (oder absolut) konvergente Reihen:

$\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }a_{\sigma (k)}$ für alle bijektiven $\sigma \colon \mathbb {N} _{0}\to \mathbb {N} _{0}$.

Bedingt konvergente Reihen dürfen nur endlich umgeordnet werden, d. h. ab einem gewissen Index muss für die Umordnung $\sigma (k)=k$ gelten.

Konvergenzkriterien

→ Hauptartikel: Konvergenzkriterium

Allgemeine Kriterien

Nullfolgenkriterium

Wenn die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ konvergiert, dann konvergiert die Folge $a_{n}$ der Summanden für $n\rightarrow \infty$ gegen 0. Kontraponiert: Ist $a_{n}$ keine Nullfolge, so divergiert die entsprechende Reihe.

Beispiel

Es kann die Reihe $\textstyle \sum _{n=0}^{\infty }(-1)^{n}=1-1+1-1+\cdots$ nicht konvergieren, da $a_{n}=(-1)^{n}$ nicht gegen 0 konvergiert.

Die Umkehrung ist nicht allgemeingültig (ein Gegenbeispiel ist die harmonische Reihe). Das Nullfolgenkriterium wird daher in erster Linie zum Nachweis der Divergenz einer Reihe verwendet.

Teleskopreihen

Die Teleskopreihe $\sum _{n=1}^{\infty }(b_{n}-b_{n+1})$ konvergiert genau dann, wenn die Folge $(b_{n})_{n\in \mathbb {N} }$ gegen eine Zahl $L$ konvergiert. Der Wert der Reihe ist dann $b_{1}-L$.

Majorantenkriterium

Wenn alle Glieder $a_{n}$ der Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ nichtnegative reelle Zahlen sind, $\textstyle \sum _{n=0}^{\infty }a_{n}$ konvergiert und für alle $n$ zudem $a_{n}\geq |b_{n}|$ gilt, dann konvergiert auch die Reihe $\textstyle \sum _{n=0}^{\infty }b_{n}$ absolut, und es ist

$\left|\sum _{n=0}^{\infty }b_{n}\right|\leq \sum _{n=0}^{\infty }a_{n}$.

Beispiel

Es konvergiert für alle $\alpha \in \mathbb {R}$ die Reihe $\textstyle \sum _{n=1}^{\infty }{\frac {\sin(\alpha n)}{n^{2}}}$. In der Tat, da $|\sin(\alpha n)|\leq 1$, folgt über $\sum _{n=1}^{\infty }\left|{\frac {\sin(\alpha n)}{n^{2}}}\right|\leq \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}<\infty$ die Behauptung mit dem Majorantenkriterium.

Minorantenkriterium

Wenn alle Glieder $a_{n}$ der Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ nichtnegative reelle Zahlen sind, $\textstyle \sum _{n=0}^{\infty }a_{n}$ divergiert und für alle $n$ zudem $a_{n}\leq b_{n}$ mit nichtnegativen reellen Zahlen $b_{n}$ gilt, dann divergiert auch die Reihe $\textstyle \sum _{n=0}^{\infty }b_{n}$.

Beispiel

Es gilt ${\frac {1}{\sqrt {n}}}\geq {\frac {1}{n}}\geq 0$ für alle $n\in \mathbb {N}$. Da nun $\sum _{n=1}^{\infty }{\frac {1}{n}}=\infty$ folgt die Divergenz der Reihe $\textstyle \sum _{n=1}^{\infty }{\frac {1}{\sqrt {n}}}$ mit dem Minorantenkriterium.

Quotientenkriterium

Es wird die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ mit $a_{n}\not =0$ für alle $n$ betrachtet. Dann gilt:

• Falls $\textstyle \limsup _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|<1$, so ist die Reihe absolut konvergent.
• Falls $\textstyle \liminf _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|>1$, so ist die Reihe divergent.
• In den verbleibenden Fällen kann keine Aussage getroffen werden, d.h. sowohl bedingte oder absolute Konvergenz aber auch Divergenz sind möglich.

Wurzelkriterium

Zu einer Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ wird die Größe $\textstyle \alpha :=\limsup _{n\to \infty }{\sqrt[{n}]{|a_{n}|}}$ betrachtet. Dann gelten folgende Aussagen:

• Ist $\alpha <1$, so konvergiert die Reihe absolut.
• Ist $\alpha >1$, so ist die Reihe divergent.
• Ist $\alpha =1$, so kann keine Aussage getroffen werden, d.h. sowohl bedingte oder absolute Konvergenz aber auch Divergenz sind möglich.

Kriterium von du Bois-Reymond und Dedekind

Dieses Kriterium kann in zwei Unterkriterien unterteilt werden.

1. Es ist die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}b_{n}$ konvergent, falls $\textstyle \sum _{n=0}^{\infty }(b_{n}-b_{n+1})$ absolut und $\textstyle \sum _{n=0}^{\infty }a_{n}$ wenigstens bedingt konvergiert.
2. Es ist die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}b_{n}$ konvergent, falls außer der absoluten Konvergenz von $\textstyle \sum _{n=0}^{\infty }(b_{n}-b_{n+1})$ lediglich die Beschränktheit der Partialsummen von $\textstyle \sum _{n=0}^{\infty }a_{n}$ und $b_{n}\to 0$ vorausgesetzt wird.

Gaußsches und Weierstraßsches Kriterium

Kann man den Quotienten ${\tfrac {a_{n+1}}{a_{n}}}$ in der Form $1-{\tfrac {\alpha }{n}}-{\tfrac {\vartheta _{n}}{n^{\lambda }}}$ mit einer beschränkten Folge $\vartheta _{n}$ und $\lambda >1$ schreiben, so ist die Reihe $\textstyle \sum _{n=1}^{\infty }a_{n}$ im Falle $\alpha >1$ konvergent, und im Falle $\alpha \leq 1$ divergent.

Dieses Kriterium von Gauß kann für komplexe Folgen ausgeweitet werden, wo es als Kriterium von Weierstraß benannt ist. Erfüllen die komplexen Glieder $a_{n}$

${\frac {a_{n+1}}{a_{n}}}=1-{\tfrac {\alpha }{n}}-{\tfrac {A_{n}}{n^{\lambda }}}$

mit $\lambda >1$ und beschränkten $A_{n}$, so konvergiert die zugehörige Reihe genau dann absolut, wenn $\mathrm {Re} (\alpha )>1$. Ist $0<\mathrm {Re} (\alpha )\leq 1$, so sind wenigstens die Reihen $\textstyle \sum _{n=1}^{\infty }|a_{n}-a_{n+1}|$ und $\textstyle \sum _{n=1}^{\infty }(-1)^{n}a_{n}$ konvergent.

Kriterien unter Monotoniebedingungen

Integralkriterium

Ist $f\colon [1,\infty )\to [0,\infty )$ eine monoton fallende Funktion mit

$f(n)=a_{n}$ für alle $n$,

dann konvergiert $S$ genau dann, wenn das uneigentliche Integral

$\int _{1}^{\infty }f(x)\,\mathrm {d} x$

existiert.

Beispiel

Die Dirichletreihe $\sum _{n=1}^{\infty }{\frac {1}{n^{r}}}$ konvergiert für $r>1$ und divergiert für $r\leq 1$, was mit dem Integralkriterium gezeigt werden kann. Als Funktion von $r$ aufgefasst, ergibt diese Reihe die Riemannsche Zetafunktion.

Leibniz-Kriterium

Eine Reihe der Form

$S=\sum _{n=0}^{\infty }(-1)^{n}a_{n}$

mit nichtnegativen $a_{n}$ wird alternierende Reihe genannt. Eine solche Reihe konvergiert, wenn die Folge $a_{n}$ monoton gegen 0 konvergiert. Die Umkehrung ist nicht allgemeingültig.

Abel-Kriterium

Es ist die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}b_{n}$ konvergent, falls die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ konvergiert, und die Folge $b_{n}$ monoton und beschränkt ist.

Dirichlet-Kriterium

Es ist die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}b_{n}$ konvergent, falls

$\sup _{N\in \mathbb {N} }\left|\sum _{n=0}^{N}a_{n}\right|<\infty ,$

mit anderen Worten, die Partialsummen sind beschränkt, und $b_{n}$ eine monoton fallende Nullfolge ist.

Cauchysches Verdichtungskriterium

Ist $a_{n}$ eine monoton fallende Nullfolge, so konvergiert die Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ genau dann, wenn die Reihe $\textstyle \sum _{n=1}^{\infty }2^{n}a_{2^{n}}$ konvergiert.

Multiplikative Funktionen

Es ist $f\colon \mathbb {N} \to \mathbb {C}$ eine multiplikative Funktion, falls $f(mn)=f(m)f(n)$ für alle teilerfremden $m$ und $n$ gilt.

Es konnte Peter D. T. A. Elliott folgendes zeigen: Ist $f$ multiplikativ, so dass

$0\not =A=\lim _{n\to \infty }{\frac {1}{n}}\sum _{m=1}^{n}f(m)$

existiert, und ferner

$\limsup _{n\to \infty }{\frac {1}{n}}\sum _{m=1}^{n}|f(m)|^{2}<\infty .$

Dann gilt bereits, dass die Reihen

$\sum _{p\ {\text{Primzahl}}}{\frac {f(p)-1}{p}},\qquad \sum _{p\ {\text{Primzahl}}}{\frac {|f(p)-1|^{2}}{p}},\qquad \sum _{p\ {\text{Primzahl}}}\sum _{k=2}^{\infty }{\frac {|f(p^{k})|}{p^{k}}}$

sämtlich konvergieren.

Funktionentheoretische Mittel

Sätze von Tauber und Littlewood

Der Satz von Tauber, bewiesen von Alfred Tauber im Jahr 1897, nutzt das Randverhalten einer Potenzreihe, um ein hinreichendes Kriterium für dortige Konvergenz zu geben. Ist

$f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}$

für alle $|z|<1$ konvergent, existiert $f(1):=\lim _{r\to 1^{-}}f(r)$ und gilt $na_{n}\to 0$ für $n\to \infty$, so konvergiert $\textstyle \sum _{n=0}^{\infty }a_{n}$ gegen $f(1)$. John Edensor Littlewood konnte dieses Resultat verbessern, indem er zeigte, dass bereits die abgeschwächte Bedingung $|na_{n}|\leq C$ für alle $n$ mit einer Konstante $C$ für die Aussage des Satzes hinreichend ist. Es konnte auch gezeigt werden, dass diese Bedingung im allgemeinen Fall nicht weiter verbessert werden kann. Wird allerdings gefordert, dass die $a_{n}$ fast alle nichtnegativ sind, kann die Bedingung der Beschränktheit von $na_{n}$ gänzlich weggelassen werden.

Kriterien von Fatou und Korevaar

Wieder habe $\textstyle f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}$ einen Konvergenzradius von mindestens 1. Gibt es sogar eine Konstante $\alpha >0$, so dass $|f(r)-f(1)|=O((1-r)^{\alpha })$ mit $r\to 1^{-}$, so folgt bereits

$\left|\sum _{k=0}^{n}a_{k}-f(1)\right|=O\left({\frac {1}{\log(n)}}\right).$

Ist $f$ um $z=1$ holomorph fortsetzbar, und gibt es eine nicht-fallende Funktion $\psi \colon \mathbb {R} \to [1,\infty )$, sodass $\psi (x)=1$ für $x\leq 0$ und $\psi (2x)\leq C\psi (x)$ für $x\geq 0$ mit einer Konstanten $C>0$. Gilt zudem $a_{n}\geq -{\tfrac {1}{\psi (n)}}$ für alle $n\geq 0$, dann konvergiert $\textstyle \sum _{n=0}^{\infty }a_{n}$ gegen $f(1)$, und zudem gilt

$\sum _{k\leq x}a_{k}=f(1)+O\left({\frac {1}{\psi (x)}}\right).$

Abel-Summierbarkeit

Man nennt eine formale Reihe $\textstyle \sum _{n=0}^{\infty }a_{n}$ Abel-summierbar gegen $A$, falls

$\lim _{r\to 1^{-}}\sum _{n=0}^{\infty }a_{n}r^{n}=A,$

wobei die Reihe zur Linken für alle $0\leq r<1$ konvergiere. Es ist eine Abel-summierbare Reihe genau dann konvergent, wenn

$\lim _{n\to \infty }{\frac {a_{1}+2a_{2}+\cdots +na_{n}}{n}}=0.$

Satz von Fatou

Der Satz Fatou besagt, dass, wenn die Potenzreihe

$f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}$

für alle $|z|<1$ konvergiert, und sich die Funktion $f$ in einer Umgebung des Randpunkts $|z_{0}|=1$ holomorph fortsetzen lässt, aus $a_{n}\to 0$ bereits folgt, dass $\textstyle \sum _{n=0}^{\infty }a_{n}$ konvergiert, und den Wert $f(z_{0})$ annimmt.

Der Satz von Fatou kann, unter Umgehung der Bedingung der Holomorphie in $z_{0}$, ausgeweitet werden. Dafür wird das Konzept des Hardy-Raums $H^{1}(D)$ eines Gebietes $D$ benötigt. Erfüllt $f$ im Randpunkt $z_{0}=e^{it_{0}}$ die lokale $H^{1}$-Bedingung, so existiert eine Zahl $\lambda >0$, sodass $f(re^{it})$ für $r\to 1^{-}$ in $L^{1}(t_{0}-\lambda ,t_{0}+\lambda )$ gegen eine (integrierbare) Funktion $t\mapsto f(e^{it})$ konvergiert (siehe auch Lp-Raum), also

$\lim _{r\to 1^{-}}\int _{t_{0}-\lambda }^{t_{0}+\lambda }|f(re^{it})-f(e^{it})|\mathrm {d} t=0.$

Ist die Menge ${\mathcal {E}}$ der Randpunkte $\zeta$, mit $|\zeta |=1$, an der $f$ singulär ist in dem Sinne, dass sie dort nicht die lokale $H^{1}$-Bedingung erfüllt, eine Nullmenge, und gilt

$\sup _{\zeta \in {\mathcal {E}}}\sup _{n\in \mathbb {N} _{0}}\left|\sum _{k=0}^{n}a_{k}\zeta ^{k}\right|=M<\infty ,$

dann konvergiert $f$ in jedem Punkt $z_{1}=e^{it_{1}}$ gegen $f(z_{1})$, an dem der Differenzenquotient

$q_{z_{1}}(z)={\frac {f(z)-f(z_{1})}{z-z_{1}}},\qquad |z|<1,$

die lokale $H^{1}$-Bedingung in $z_{1}$ erfüllt.

Satz von Ingham

Ein im Jahr 1935 gegebener Satz von Albert Ingham war Ausgangspunkt für weitere Untersuchungen von Donald Newman, der diesen mit einfachen funktionentheoretischen Mitteln beweisen konnte. Sei eine Dirichlet-Reihe

$f(s)=\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}$

für alle $s$ mit $\mathrm {Re} (s)>1$ konvergent (d.h. sie stellt in dieser offenen Halbebene eine holomorphe Funktion dar). Lässt sich $f$ nun holomorph auf eine offene Menge fortsetzen, die $\{s\in \mathbb {C} \colon \mathrm {Re} (s)\geq 1\}$ vollständig enthält, und sind die $a_{n}$ beschränkt, so gilt bereits für alle $t\in \mathbb {R}$

$\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{1+it}}}=f(1+it).$

Für unbeschränkte $a_{n}$ ist die obere Aussage bekanntlich falsch.

Methoden zur Grenzwertbestimmung

Es existiert kein allgemeines Verfahren, den Grenzwert einer konvergenten Reihe explizit auszurechnen. In einigen Fällen lassen sich Grenzwerte auch nicht auf „elementare“ mathematische Konstanten zurückführen, etwa im Fall der Apery-Konstante

$\zeta (3):=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}.$

Allerdings gibt es einige Techniken, die in speziellen Situationen die geschlossene Berechnung eines konvergenten Reihenausdrucks ermöglichen.

Abelscher Grenzwertsatz

→ Hauptartikel: Abelscher Grenzwertsatz

Es sei $\textstyle \sum _{n=0}^{\infty }a_{n}$ eine konvergente Reihe. Eine Möglichkeit, ihren Grenzwert zu bestimmen, geht über die von den $a_{n}$ erzeugte Funktion. Niels Henrik Abel konnte beweisen, dass sich die Funktion

$f(x):=\sum _{n=0}^{\infty }a_{n}x^{n}$

stetig nach $x=1$ fortsetzen lässt. Ferner gilt

$f(1)=\sum _{n=0}^{\infty }a_{n}.$

Mit diesem Ansatz können manche klassischen Reihengrenzwerte berechnet werden. Beispielsweise gilt für alle $x$ mit $|x|<1$ gilt die Reihendarstellung

$\arctan(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n+1}}{2n+1}}.$

Mit dem Leibniz-Kriterium und der Abel-Summierbarkeit folgt damit die Leibniz-Reihe:

$\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots =\arctan(1)={\frac {\pi }{4}}.$

Ähnlich verhält es sich mit der Taylor-Reihe des natürlichen Logarithmus: $\log(1+x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{n+1}}{n+1}}.$ Damit folgt, dass die alternierende harmonische Reihe den Grenzwert $\log(2)$ besitzt:

$\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\cdots =\log(2).$

Fourier-Analysis

Die Grenzwertbestimmung über Fourier-Reihen ähnelt sich mit dem Grenzwertsatz von Abel insofern, als das die Reihe auch hier als Wert einer zu bestimmenden Funktion interpretiert wird. Weiß man, dass $\textstyle \sum _{n=-\infty }^{\infty }a_{n}$ absolut konvergiert, so kann man ihren Wert als $f(0)$ mit

$f(x):=\sum _{n=-\infty }^{\infty }a_{n}e^{2\pi ixn}$

auffassen. Dann ist $f$ eine 1-periodische Funktion, und die rechte Seite ihre Darstellung als Fourier-Reihe. Über die Umrechungsformel

$a_{n}=\int _{0}^{1}f(x)e^{-2\pi inx}\mathrm {d} x$

können die Koeffizienten der Reihe aus $f$ zurückgewonnen werden. Es muss also ein „passendes“ $f$ zu den $a_{n}$ gefunden werden. Zum Beispiel findet man mit partieller Integration schnell

${\frac {(\pi -x)^{2}}{4}}={\frac {\pi ^{2}}{12}}+\sum _{n=1}^{\infty }{\frac {\cos(xn)}{n^{2}}},$

womit durch Einsetzen von $x=0$ die Antwort auf das Basler Problem folgt. Ist $f$ lediglich als auf dem Intervall $[0,1]$ integrierbar vorausgesetzt, und hat die assoziierte Fourier-Reihe $\textstyle \sum _{n=-\infty }^{\infty }a_{n}e^{2\pi ixn}$, so gilt außerdem die Parsevalsche Identität

$\sum _{n=-\infty }^{\infty }|a_{n}|^{2}=\int _{0}^{1}|f(x)|^{2}\mathrm {d} x.$

Gelten für $f\colon \mathbb {R} \to \mathbb {C}$ geeignete Wachstumsbedingungen, ist es zum Beispiel eine Schwartz-Funktion, so gilt ferner die Poissonsche Summationsformel:

$\sum _{n=-\infty }^{\infty }f(n)=\sum _{n=-\infty }^{\infty }{\hat {f}}(n).$

Diese ermöglicht es, eine Reihe über Funktionswerte an ganzen Stellen in jene bezüglich der Fourier-Transformierten

${\hat {f}}(x):=\int _{-\infty }^{\infty }f(y)e^{-2\pi ixy}\mathrm {d} y$

umzuwandeln, und umgekehrt.

Residuensatz

In manchen Fällen, besonders bei unendlichen Reihen über rationale Funktionen, kann der Residuensatz aus der Funktionentheorie verwendet werden. Ist $f\colon \mathbb {C} \to {\overline {\mathbb {C} }}$ eine meromorphe Funktion mit endlichen vielen, nicht ganzzahligen Polstellen $z_{1},...,z_{n}$, so gilt, falls zusätzlich $f(z)=O(|z|^{-\nu })$ mit $|z|\to \infty$ und $\nu >1$, die Formel

$\sum _{k=-\infty }^{\infty }f(k)=-\sum _{j=1}^{n}\mathrm {Res} _{z=z_{j}}\left(\pi \cot(\pi z)f(z)\right).$

Ähnlich gilt

$\sum _{k=-\infty }^{\infty }(-1)^{k}f(k)=-\sum _{j=1}^{n}\mathrm {Res} _{z=z_{j}}\left(\pi \csc(\pi z)f(z)\right).$

Dabei bezeichnet $\cot$ den Kotangens und $\csc$ den Kosekans. Diese Aussage beinhaltet folgenden Spezialfall: Sind $P(z)$ und $Q(z)$ Polynome, so dass $\deg(Q)\geq \deg(P)+2$ und $Q(k)\not =0$ für alle $k\in \mathbb {Z}$, so folgt

$\sum _{k=-\infty }^{\infty }{\frac {P(k)}{Q(k)}}=-\sum _{Q(w)=0}\mathrm {Res} _{z=w}\left({\frac {\pi \cot(\pi w)P(z)}{Q(z)}}\right).$

Mit diesem Verfahren lässt sich zum Beispiel

$\sum _{k=-\infty }^{\infty }{\frac {1}{k^{2}+1}}=\pi \coth(\pi )=\pi {\frac {e^{2\pi }+1}{e^{2\pi }-1}}$

und

$\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}}{k^{2}+1}}=\pi \ \mathrm {csch} (\pi )=\pi {\frac {2e^{\pi }}{e^{2\pi }-1}}$

zeigen.

Ungleichungen

Ungleichungen für Reihen verwenden oft spezielle analytische Methoden, etwa aus der Fourier-Analysis.

Standardabschätzung

Es gilt stets

$\left|\sum _{n=1}^{\infty }a_{n}\right|\leq \sum _{n=1}^{\infty }|a_{n}|.$

Besselsche Ungleichung

Bezeichnet $f\colon \mathbb {R} \to \mathbb {C}$ eine 1-periodische Funktion und ${\hat {f}}$ ihre Fourier-Transformierte, so gilt die Besselsche Ungleichung

$\sum _{n=-\infty }^{\infty }|{\hat {f}}(n)|^{2}\leq \int _{0}^{1}|f(x)|^{2}\mathrm {d} x.$

Hausdorff-Young-Ungleichung

Sind $1\leq p\leq 2$ und $q$ so gewählt, dass ${\tfrac {1}{p}}+{\tfrac {1}{q}}=1$, so gilt die Hausdorff-Young-Ungleichung

$\left(\sum _{n=-\infty }^{\infty }|a_{n}|^{q}\right)^{\frac {1}{q}}\leq \left(\int _{0}^{1}|f(x)|^{p}\mathrm {d} x\right)^{\frac {1}{p}}$

und ihre „Duale“

$\left(\int _{0}^{1}|f(x)|^{q}\mathrm {d} x\right)^{\frac {1}{q}}\leq \left(\sum _{n=-\infty }^{\infty }|a_{n}|^{p}\right)^{\frac {1}{p}}$

wenn $f\colon \mathbb {R} \to \mathbb {C}$ 1-periodisch, auf $[0,1]$ integrierbar mit assoziierter Fourier-Reihe $\textstyle \sum _{n=-\infty }^{\infty }a_{n}e^{2\pi ixn}$.

Anwendungen

Darstellung mathematischer Konstanten

Neben der Konvergenz und dem numerischen Wert einer Reihe ist auch der symbolische Wert einer Reihe von Bedeutung. Beispielsweise lassen sich so mathematische Konstanten darstellen und numerisch berechnen. Für wichtige Reihendarstellungen existieren zudem Tabellierungen in Reihentafeln.

Kreiszahl

Von historischer Bedeutung ist etwa das Basler Problem, welches nach dem Grenzwert der Reihe $1+{\tfrac {1}{4}}+{\tfrac {1}{9}}+\cdots$ aller reziproken Quadratzahlen fragte. Leonhard Euler publizierte 1735 in seiner De Summis Serierum Reciprocarum die Lösung:

${\frac {\pi ^{2}}{6}}=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}.$

Dabei ist $\pi =3{,}14\ldots$ die Kreiszahl. Euler konnte allgemein für $k\in \mathbb {N}$ sogar

$(-1)^{k-1}{\frac {(2\pi )^{2k}}{2(2k)!}}B_{2k}=\sum _{n=1}^{\infty }{\frac {1}{n^{2k}}}$

mit den Bernoulli-Zahlen $B_{k}$ zeigen. Der Fall ungerader Exponenten ist deutlich schwieriger, und es existieren hier keine geschlossenen Analoga. Allerdings konnte Matyáš Lerch im Jahr 1900 folgende Reihenidentität aufzeigen:

${\frac {7\pi ^{3}}{180}}=\sum _{n=1}^{\infty }\left({\frac {1}{n^{3}}}+{\frac {2}{n^{3}(e^{2\pi n}-1)}}\right).$

Während all diese Reihen vergleichsweise langsam konvergieren, ist die 1914 von Srinivasa Ramanujan veröffentlichte, auf Untersuchungen von elliptischen Funktionen und Modulfunktionen basierende Gleichung zur Berechnung der Kreiszahl gut geeignet:

${\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{n=0}^{\infty }\,{\frac {(4n)!(1103+26390\,n)}{(n!)^{4}\,396^{4n}}}.$

Die Brüder David und Gregory Chudnovsky berechneten mit ihrer Hilfe 2 Milliarden Nachkommastellen von $\pi$ in den frühen neunziger Jahren. Der davon inspirierte Chudnovsky-Algorithmus basiert auf der folgenden verwandten Reihendarstellung:

${\frac {1}{\pi }}={\frac {\sqrt {10005}}{4270934400}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}(6n)!(545140134n+13591409)}{(3n)!\,(n!)^{3}\,640320^{3n}}}.\!$

1995 entdeckte Simon Plouffe zusammen mit Peter Borwein und David Harold Bailey die Bailey-Borwein-Plouffe-Formel:

$\pi =\sum _{n=0}^{\infty }{\dfrac {1}{16^{n}}}\left({\dfrac {4}{8n+1}}-{\dfrac {2}{8n+4}}-{\dfrac {1}{8n+5}}-{\dfrac {1}{8n+6}}\right).$

Diese Reihe ermöglicht es, die $n$-te Stelle einer binären, hexadezimalen oder beliebigen Darstellung zu einer Zweierpotenz-Basis von $\pi$ zu berechnen, ohne dass zuvor die $n-1$ vorherigen Ziffernstellen berechnet werden müssen.

Eulersche Zahl

Die Eulersche Zahl $e=2{,}718\ldots$ ist die Basis des natürlichen Logarithmus. Ihre bekannteste Reihendarstellung ergibt sich aus der Taylor-Entwicklung der natürlichen Exponentialfunktion:

$e=\sum _{n=0}^{\infty }{\frac {1}{n!}}=1+1+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots .$

Aufgrund ihrer schnellen Konvergenz ist diese Reihe nicht nur zur Berechnung von Dezimalstellen der Eulerschen Zahl geeignet. Es kann mit ihrer Hilfe auch ein elementarer Beweis erbracht werden, dass $e$ eine irrationale Zahl ist.

Darstellung und Näherung von Funktionen

Wichtige Typen von Reihendarstellungen

Dirichlet-Reihen

→ Hauptartikel: Dirichlet-Reihe

Reihen des Typs

$\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}$

werden als Dirichlet-Reihen bezeichnet. Dabei ist $s$ eine komplexe Variable. Konvergiert eine Dirichlet-Reihe an der Stelle $s_{0}$, so ist sie bereits an allen Stellen $s$ mit $\mathrm {Re} (s)>\mathrm {Re} (s_{0})$ konvergent. Dies kann mit Abelscher partieller Summation gezeigt werden. In offenen Teilbereichen ihres Konvergenzberechs stellen sie holomorphe Funktionen dar. Sie können aber auch ohne Konvergenzfragen als formale Objekte studiert werden.

Verallgemeinerung

Definition über Banachräume

Es sei $E$ ein Banachraum und $(x_{j})_{j\in \mathbb {N} _{0}}$ eine Folge in $E$. Dann definieren wir eine neue Folge $(s_{n})_{n\in \mathbb {N} _{0}}$ in $E$ durch

$s_{n}:=\sum _{j=0}^{n}x_{j}.$

Diese heißt Reihe in $E$. Sie heißt konvergent, wenn die Folge der Partialsummen konvergiert, wobei hier die zu $E$ gehörige Norm $|.|_{E}$ genutzt wird. Auch in diesem Fall gilt die oben erklärte Korrespondenz zwischen Folgen und Reihen, wobei erneut die rekursive Bauart zu Vorteilen bei der Formulierung von Konvergenzkriterien führt.

Weblinks

Wikibooks: Mathe für Nicht-Freaks: Reihe – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Konvergenz einer Reihe – Lern- und Lehrmaterialien

Literatur

• Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 6. Auflage. Springer, Berlin u. a. 1996, ISBN 3-540-59111-7, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 2).
• Izrail Solomonovic Gradshteyn, Iosif Mojseevic Ryzhik: Table of Integrals, Series and Products. Herausgegeben von Alan Jeffrey und Daniel Zwillinger. 7. Ausgabe. Elsevier Academic Press, Amsterdam u. a. 2007, ISBN 978-0-12-373637-6.

Einzelnachweise

!Reihe