Triakisikosaeder

Das Triakisikosaeder ist ein konvexes Polyeder, das sich aus 60 gleichschenkligen Dreiecken zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum Dodekaederstumpf und hat 32 Ecken sowie 90 Kanten.

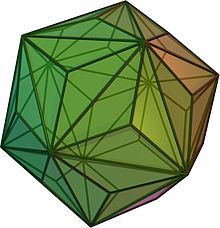
3D-Ansicht eines Triakisikosaeders (Animation)

EntstehungBearbeiten

Werden auf die 20 Begrenzungsflächen eines Ikosaeders (Kantenlänge $a$ ) Pyramiden mit der Flankenlänge $b$ aufgesetzt, entsteht ein Triakisikosaeder, sofern folgende Bedingung erfüllt ist:

{\frac {a}{3}}{\sqrt {3}}<b<{\frac {a}{4}}{\sqrt {10-2{\sqrt {5}}}}

Für den zuvor genannten minimalen Wert von $b$ haben die aufgesetzten Pyramiden die Höhe 0, sodass lediglich das Ikosaeder mit der Kantenlänge $a$ übrig bleibt.
Das spezielle Triakisikosaeder mit gleichen Flächenwinkeln entsteht, wenn $b={\frac {a}{22}}\,(15-{\sqrt {5}})$ ist.
Nimmt $b$ den o. g. maximalen Wert an, entartet das Triakisikosaeder zu einem Rhombentriakontaeder mit der Kantenlänge $b$ .
Überschreitet $b$ den maximalen Wert, so ist das Polyeder nicht mehr konvex und entartet schließlich für $b={\frac {a}{2}}\left(1+{\sqrt {5}}\right)$ zum Ikosaederstern.

FormelnBearbeiten

AllgemeinBearbeiten

Größen eines Triakisikosaeders mit Kantenlängen a, b
Volumen	$V={\frac {5}{12}}a^{2}\left(a(3+{\sqrt {5}})+4{\sqrt {3b^{2}-a^{2}}}\right)$
Oberflächeninhalt	$A_{O}=15a{\sqrt {4b^{2}-a^{2}}}$
Pyramidenhöhe	$k={\frac {1}{3}}{\sqrt {9b^{2}-3a^{2}}}$
Inkugelradius	$\rho ={\frac {a}{4}}{\sqrt {{\frac {10a+4b}{a+2b}}+2{\sqrt {5}}}}$
Flächenwinkel (über Kante a)	$\cos \,\alpha _{1}={\frac {(12b^{2}-5a^{2}){\sqrt {5}}-8a{\sqrt {3b^{2}-a^{2}}}}{9(4b^{2}-a^{2})}}$
Flächenwinkel (über Kante b)	$\cos \,\alpha _{2}={\frac {2b^{2}-a^{2}}{4b^{2}-a^{2}}}$

^[1]

SpeziellBearbeiten

Kantenkugel im speziellen Triakisikosaeder: Deutlich treten die Kugelkappen auf den einzelnen Dreiecksflächen hervor. Die Inkreise sind zugleich Schnittflächen der Dreiecke mit der Kantenkugel.

Größen eines Triakisikosaeders mit Kantenlänge a
Volumen	$V={\frac {5}{44}}a^{3}(5+7{\sqrt {5}})$
Oberflächeninhalt	$A_{O}={\frac {15}{11}}a^{2}{\sqrt {109-30{\sqrt {5}}}}$
2. Seitenlänge ≈ 0,5802 · a	$b={\frac {a}{22}}\,(15-{\sqrt {5}})$
Pyramidenhöhe	$k={\frac {a}{66}}(5{\sqrt {5}}-9){\sqrt {3}}$
Inkugelradius	$\rho ={\frac {a}{4}}{\sqrt {\frac {10(33+13{\sqrt {5}})}{61}}}$
Kantenkugelradius	$r={\frac {a}{4}}\left(1+{\sqrt {5}}\right)$
Flächenwinkel ≈ 160° 36′ 45″	$\cos \,\alpha =-{\frac {1}{61}}(24+15{\sqrt {5}})$
Sphärizität ≈ 0,96734	$\Psi ={\frac {\sqrt[{3}]{396\,\pi \left(27+7{\sqrt {5}}\right)}}{6{\sqrt {109-30{\sqrt {5}}}}}}$