Urbild (Mathematik)
In der Mathematik ist das Urbild ein Begriff, der im Zusammenhang mit Funktionen verwendet wird. Für eine Funktion ist das Urbild einer Menge jene Teilmenge der Definitionsmenge , deren Elemente auf die vorher festgelegte Untermenge der Zielmenge abgebildet werden. Das Urbild ist also die Antwort auf die Frage: Welche Elemente aus der Definitionsmenge werden auf Elemente der Menge abgebildet? Man sagt dann auch Urbild von unter .
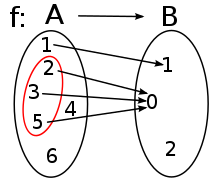
Das Urbild eines einzelnen Elements der Zielmenge ist die aus allen mit bestehende Teilmenge der Definitionsmenge. Das Urbild der Bildmenge (und natürlich erst recht der ganzen Zielmenge ) ist genau die Definitionsmenge , da Funktionen linkstotal sind, also jedem Element der Definitionsmenge mindestens ein Element der Zielmenge (und genau ein Element der Bildmenge) zuordnen.
Definition
BearbeitenSei eine Funktion und eine Teilmenge von . Dann bezeichnet man die Menge
als das Urbild von M unter f.
Ein Urbild ist damit ein Wert der sogenannten Urbildfunktion , die jedem Element der Potenzmenge der Zielmenge das Urbild als Element der Potenzmenge der Definitionsmenge zuordnet.
Das Urbild einer einelementigen Menge schreibt man auch als
und nennt es das Urbild von b unter f. Diese Menge braucht aber nicht einelementig zu sein (sie kann also auch leer sein oder mehr als ein Element enthalten).
Das Urbild eines Elements wird zuweilen auch Faser der Abbildung über diesem Element genannt, insbesondere im Zusammenhang mit Faserbündeln.
Beispiele
BearbeitenFür die Funktion (ganze Zahlen) mit gilt:
Eigenschaften
BearbeitenInjektivität, Surjektivität, Bijektivität
Bearbeiten- Unter einer bijektiven Funktion ist das Urbild jedes Elements (genau) einelementig. Die Abbildung , die jedem Element von das (einzige, also eindeutig bestimmte) Element seines Urbildes zuordnet, heißt Umkehrfunktion von . Man bezeichnet sie also wie auch die Urbildfunktion mit . Das kann leicht zu Missverständnissen führen, wenn man nicht ausführlich für die Umkehrfunktion und für die Urbildfunktion schreibt und so beide deutlich unterscheidet.
- Unter einer injektiven Funktion ist das Urbild jedes Elements höchstens einelementig (also einelementig oder leer).
- Unter einer surjektiven Funktion ist das Urbild jedes Elements mindestens einelementig (also nichtleer).
Mengenoperationen und -eigenschaften
BearbeitenEs sei eine Funktion, und und seien Teilmengen von . Dann gilt:
-
Insbesondere haben also disjunkte Mengen disjunkte Urbilder.
Die letzten beiden Aussagen (über Vereinigung und Durchschnitt) lassen sich von zwei Teilmengen auf beliebige Familien von Teilmengen verallgemeinern. -
Dabei bezeichnet das Komplement von in der jeweiligen Grundmenge .
Bild und Urbild
BearbeitenEs sei eine Funktion, eine Teilmenge von und eine Teilmenge von . Dann gilt:
-
d. h., es liegt eine Galoisverbindung vor. -
Ist injektiv, dann gilt die Gleichheit. -
Ist surjektiv, dann gilt die Gleichheit. Hinreichend ist schon , dass also eine Teilmenge des Bildes von ist.
Urbild und Komposition
BearbeitenFür beliebige Mengen und beliebige Funktionen bezeichne die Komposition von mit .
Dann gilt für jede Teilmenge :












