Benutzer:Mini-floh/TestArtikel

Formatierung von Mathematischen Formeln

Blablbla blabla blabla blblablabla blabla blbla blablabla blablbla bla b lablablablb lablablabla b l ablblablablablabl a blblabl abla blabla
Buchstabengröße: $A\preccurlyeq B$, ${\mathfrak {A}}\preccurlyeq {\mathfrak {B}}$ oder so: $\textstyle A\preccurlyeq B$; nächster Versuch: $\displaystyle {\mathfrak {A}}\preccurlyeq {\mathfrak {B}}$
Blablblablablablablablblabla blablabla bl blabla blablablabl blablabla blablablbl ab lablablabl abl blablablabla b l ablblabla blabl abla
Blablblabla blablablablbla blablablablabl bla blablablab lablblablabla blablabl blablabla blablablblabla blablablabl blablablablabla
Ausrichtung: ${\mathfrak {A}}\preccurlyeq {\mathfrak {B}}$ gegen ^{$\displaystyle {\mathfrak {A}}\preccurlyeq {\mathfrak {B}}$} und _{$\displaystyle {\mathfrak {A}}\preccurlyeq {\mathfrak {B}}$}
Blabl blablablablablablbla blablablablablblabla bla blablablblablablablablablblablabla blablabl blablablablablablbla blablablabla
Wieder neuer Versuch(07.02.): $\textstyle {\mathfrak {A}}\preccurlyeq {\mathfrak {B}}$ Blablblablablablablablblabla blablabla bl blabla blablablabl blablabla blablablbl ab lablablabl abl blablablabla b l ablblabla blabl abla
Blablblabla blablablablbla blablablablabl bla blablablab lablblablabla blablabl blablabla blablablblabla blablablabl blablablablabla

(immer noch Schrott; nur Hoch- und Tiefstellung funktionieren, dann aber zu stark.)

Gallerien und „Mehrere Bilder“

• Hasse-Diagramme für einige Verbände
• 
  "Verband der Teilmengen von $\{x,y,z\}$"
• 
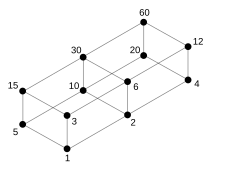
  "Verband der Teiler von 60"
• 
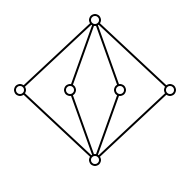
  "Partitionen der Menge {1,2,3,4}, durch "gröber=größer" geordnet"
• 

Breitenanpassung, damit alle gleiche Höhe haben:

{{#expr: (dh * ow / oh) round 0}} where

dh is the desired height in pixels

ow is the original width in pixels

oh is the original height in pixels

Hasse-Diagramme für einige Verbände

Verband der Teilmengen von {x,y,z}

Verband der Teiler von 60

Partitionen der Menge {1,2,3,4}, durch "gröber=größer" geordnet

Ideal (Verbandstheorie)

Ein Ideal $I$ ist eine spezielle Unterstruktur eines Verbandes .

Ideale spielen, ähnlich wie in der Ringtheorie, ein Rolle bei der Beschreibung von Äquivalenzrelationen auf und bei Homomorphismen zwischen Verbänden.

In Verbänden gibt es zusätzlich zu Idealen noch duale Strukturen, die Filter heißen. Auch diese können zur Erzeugung von Äquivalenzrelationen verwendet werden. Es hängt von der jeweiligen Anwendung ab, ob man mit Filtern oder mit Idealen arbeitet.

In der Topologie werden eher Filter verwendet, weil die Umgebungen eines Punktes einen Filter bilden.

Präzisierung

Ideale als algebraische Strukturen

Datei:Bild für ein Ideal und ein Nicht-Ideal

Ein Ideal $I$ in einem Verband ist eine Unterstruktur, für die gilt:

• $I$ ist Unterverband, d. h. mit $a,b\in I$ sind auch $a\sqcup b$ und $a\sqcap b\in I$
• sind $a\in I$ und $x\in V$, dann ist $a\sqcap x\in I$.

(Die Definition entspricht also formal der Definition, die man in einem Ring verwendet).

Ideale als Ordnung-Strukturen

Ein Ideal $I$ in einem Verband ist ein Teilmenge, für die gilt:

• $I$ ist nach oben gerichtet, d. h. sind $a,b\in V$, dann gibt es ein $c\in V$ mit $a\leq c$ und $b\leq c$
• ist $a\in I$ und $b\leq a\in V$, dann ist auch $b\in I$, d. h. $I$ xxxxxxx

Äquivalenz der Beschreibungen

Man sieht sehr einfach, dass beide Definitionen äquivalent sind:

Hat man eine Unterstruktur, die die erste Definition erfüllt, dann ist $a\sqcup b$ natürlich ein Element, das größer als sowohl a als auch b ist. Ist b < a mit $a\in I$, dann ist $b=b\sqcap a$ und daher auch in I.
Die Umkehrung folgt genauso einfach.

Man verwendet in der Beschreibung eines Ideals häufig eine „Mischung“ aus beiden Definitionen und sagt:

Ein Ideal ist ein Unterverband, der mit jedem Element auch alle kleineren Elemente enthält.

Man kann Ideale auch mit Hilfe einer einzigen Bedingung beschreiben:

„Eine nicht-leere Teilmenge I von V ist ein Ideal“ ist gleichwertig mit:

• Für alle $a,b,\in V$ ist $a,b\in V\quad \Longleftrightarrow \quad a\sqcup b\in V$

Filter

Datei:Bild für ein Ideal und den dualen Filter

Filter werden dual zu Idealen definiert. Die zusammenfassende Form heißt hier:

• ein Filter ist ein Unterverband, der zusammen mit einem Element a auch alle Elemente von V enthält, die größer als a sind.

Spezielle Filter und Ideale

Triviale Filter und Ideale

Ganz V erfüllt die Definition für einen Filter; hat V ein maximales Element 1, dann ist $\{1\}$ ein Filter. Diese beiden werden meist als "triviale Filter" bezeichnet.

Ganz V erfüllt auch die Definition für ein Ideal; hat V ein minimales Element 0, dann ist $\{0\}$ ein Ideal. Diese beiden werden meist als "triviale Ideale" bezeichnet.

Hauptideale und Hauptfilter

Ist $a\in V$ beliebig, dann bildet die Menge $x\in V|x\geq a$ einen Filter. Ein Filter dieser Form heißt Hauptfilter und a das erzeugende Element dieses Filters.

Man sieht wieder, dass die duale Struktur, das von a erzeugte Ideal, der Verwendung des Begriffs in der Ringtheorie entspricht.

Freie und fixierte Ideale und Filter

Ein Filter F heißt fixiert, wenn inf F > 0 ist. Ein Filter, der nicht fixiert ist, heißt freier Filter

Hauptfilter sind fixiert durch ihr erzeugendes Element. In der Menge P(N) bilden die endlichen Mengen ein freies Ideal. Der hierzu duale Filter, der aus genau den Mengen besteht, deren Komplement endlich ist („koendliche Mengen“) wird auch Fréchet-Filter genannt.

Primideale und Primfilter

Die Deinition eines Primideals entspricht wieder formal der des

Maximale Ideale und Ultrafilter

Ein Ideal I heißt maximales Ideal, wenn es kein nicht-triviales Ideal gibt, das I echt erweitert.

Jedes maximale Ideal ist ein Primideal, aber nicht jedes Primideal ist maximal.

Dual hierzu definiert man Ultrafilter:

Existenz von Idealen und Filtern

BPI

Siehe auch

• Filter (Mathematik)
• Ideal (Mathematik)
• Primideal
• Maximales Ideal
• Ultrafilter

Einzelnachweise

[[Kategorie:Verbandstheorie]]