Ein pythagoreisches Quadrupel [1] Tupel von ganzen Zahlen
a
,
b
,
c
,
d
∈
Z
{\displaystyle a,b,c,d\in \mathbb {Z} }
Alle vier primitiven pythagoreischen Quadrupel mit einstelligen Werten
a
2
+
b
2
+
c
2
=
d
2
{\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}
Es handelt sich dabei um die Lösungen einer diophantischen Gleichung . Meistens werden aber nur positive ganze Zahlen als Lösungen betrachtet.[2]
Primitive pythagoreische Quadrupeln
Bearbeiten
Ein pythagoreisches Quadrupel
(
a
,
b
,
c
,
d
)
{\displaystyle (a,b,c,d)}
primitives pythagoreisches Quadrupel , wenn die Werte positiv ganzzahlig sind und der größte gemeinsame Teiler der vier Werte gleich 1 ist (wenn also
ggT
(
a
,
b
,
c
,
d
)
=
1
{\displaystyle \operatorname {ggT} (a,b,c,d)=1}
Beispiel 1:
Das Tupel
(
a
,
b
,
c
,
d
)
=
(
2
,
3
,
6
,
7
)
{\displaystyle (a,b,c,d)=(2,3,6,7)}
ggT
(
2
,
3
,
6
,
7
)
=
1
{\displaystyle \operatorname {ggT} (2,3,6,7)=1}
2
2
+
3
2
+
6
2
=
7
2
(
=
49
)
{\displaystyle 2^{2}+3^{2}+6^{2}=7^{2}\quad (=49)}
Beispiel 2:
Das Tupel
(
a
,
b
,
c
,
d
)
=
(
5
⋅
2
,
5
⋅
3
,
5
⋅
6
,
5
⋅
7
)
=
(
10
,
15
,
30
,
35
)
{\displaystyle (a,b,c,d)=(5\cdot 2,5\cdot 3,5\cdot 6,5\cdot 7)=(10,15,30,35)}
kein primitives pythagoreisches Quadrupel, weil
ggT
(
10
,
15
,
30
,
35
)
=
5
≠
1
{\displaystyle \operatorname {ggT} (10,15,30,35)=5\not =1}
10
2
+
15
2
+
30
2
=
35
2
(
=
1225
)
{\displaystyle 10^{2}+15^{2}+30^{2}=35^{2}\quad (=1225)}
Es gibt 31 primitive pythagoreische Quadrupel, bei denen alle Werte kleiner als 30 sind:
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
d
{\displaystyle d}
a
2
+
b
2
+
c
2
=
d
2
{\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}
1
2
2
3
1
2
+
2
2
+
2
2
=
3
2
{\displaystyle 1^{2}+2^{2}+2^{2}=3^{2}}
2
3
6
7
2
2
+
3
2
+
6
2
=
7
2
{\displaystyle 2^{2}+3^{2}+6^{2}=7^{2}}
1
4
8
9
1
2
+
4
2
+
8
2
=
9
2
{\displaystyle 1^{2}+4^{2}+8^{2}=9^{2}}
4
4
7
9
4
2
+
4
2
+
7
2
=
9
2
{\displaystyle 4^{2}+4^{2}+7^{2}=9^{2}}
2
6
9
11
2
2
+
6
2
+
9
2
=
11
2
{\displaystyle 2^{2}+6^{2}+9^{2}=11^{2}}
6
6
7
11
6
2
+
6
2
+
7
2
=
11
2
{\displaystyle 6^{2}+6^{2}+7^{2}=11^{2}}
3
4
12
13
3
2
+
4
2
+
12
2
=
13
2
{\displaystyle 3^{2}+4^{2}+12^{2}=13^{2}}
2
5
14
15
2
2
+
5
2
+
14
2
=
15
2
{\displaystyle 2^{2}+5^{2}+14^{2}=15^{2}}
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
d
{\displaystyle d}
a
2
+
b
2
+
c
2
=
d
2
{\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}
2
10
11
15
2
2
+
10
2
+
11
2
=
15
2
{\displaystyle 2^{2}+10^{2}+11^{2}=15^{2}}
1
12
12
17
1
2
+
12
2
+
12
2
=
17
2
{\displaystyle 1^{2}+12^{2}+12^{2}=17^{2}}
8
9
12
17
8
2
+
9
2
+
12
2
=
17
2
{\displaystyle 8^{2}+9^{2}+12^{2}=17^{2}}
1
6
18
19
1
2
+
6
2
+
18
2
=
19
2
{\displaystyle 1^{2}+6^{2}+18^{2}=19^{2}}
6
6
17
19
6
2
+
6
2
+
17
2
=
19
2
{\displaystyle 6^{2}+6^{2}+17^{2}=19^{2}}
6
10
15
19
6
2
+
10
2
+
15
2
=
19
2
{\displaystyle 6^{2}+10^{2}+15^{2}=19^{2}}
4
5
20
21
4
2
+
5
2
+
20
2
=
21
2
{\displaystyle 4^{2}+5^{2}+20^{2}=21^{2}}
4
8
19
21
4
2
+
8
2
+
19
2
=
21
2
{\displaystyle 4^{2}+8^{2}+19^{2}=21^{2}}
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
d
{\displaystyle d}
a
2
+
b
2
+
c
2
=
d
2
{\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}
4
13
16
21
4
2
+
13
2
+
16
2
=
21
2
{\displaystyle 4^{2}+13^{2}+16^{2}=21^{2}}
8
11
16
21
8
2
+
11
2
+
16
2
=
21
2
{\displaystyle 8^{2}+11^{2}+16^{2}=21^{2}}
3
6
22
23
3
2
+
6
2
+
22
2
=
23
2
{\displaystyle 3^{2}+6^{2}+22^{2}=23^{2}}
3
14
18
23
3
2
+
14
2
+
18
2
=
23
2
{\displaystyle 3^{2}+14^{2}+18^{2}=23^{2}}
6
13
18
23
6
2
+
13
2
+
18
2
=
23
2
{\displaystyle 6^{2}+13^{2}+18^{2}=23^{2}}
9
12
20
25
9
2
+
12
2
+
20
2
=
25
2
{\displaystyle 9^{2}+12^{2}+20^{2}=25^{2}}
12
15
16
25
12
2
+
15
2
+
16
2
=
25
2
{\displaystyle 12^{2}+15^{2}+16^{2}=25^{2}}
2
7
26
27
2
2
+
7
2
+
26
2
=
27
2
{\displaystyle 2^{2}+7^{2}+26^{2}=27^{2}}
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
d
{\displaystyle d}
a
2
+
b
2
+
c
2
=
d
2
{\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}
2
10
25
27
2
2
+
10
2
+
25
2
=
27
2
{\displaystyle 2^{2}+10^{2}+25^{2}=27^{2}}
2
14
23
27
2
2
+
14
2
+
23
2
=
27
2
{\displaystyle 2^{2}+14^{2}+23^{2}=27^{2}}
7
14
22
27
7
2
+
14
2
+
22
2
=
27
2
{\displaystyle 7^{2}+14^{2}+22^{2}=27^{2}}
10
10
23
27
10
2
+
10
2
+
23
2
=
27
2
{\displaystyle 10^{2}+10^{2}+23^{2}=27^{2}}
3
16
24
29
3
2
+
16
2
+
24
2
=
29
2
{\displaystyle 3^{2}+16^{2}+24^{2}=29^{2}}
11
12
24
29
11
2
+
12
2
+
24
2
=
29
2
{\displaystyle 11^{2}+12^{2}+24^{2}=29^{2}}
12
16
21
29
12
2
+
16
2
+
21
2
=
29
2
{\displaystyle 12^{2}+16^{2}+21^{2}=29^{2}}
Aus diesen primitiven pythagoreischen Quadrupeln kann man beliebig viele weitere nicht-primitive pythagoreische Quadrupel bilden. Zum Beispiel kann man aus dem primitiven pythagoreischen Quadrupel
(
a
,
b
,
c
,
d
)
=
(
1
,
2
,
2
,
3
)
{\displaystyle (a,b,c,d)=(1,2,2,3)}
2
,
3
,
4
,
…
{\displaystyle 2,3,4,\ldots }
(
a
,
b
,
c
,
d
)
=
(
2
,
4
,
4
,
6
)
{\displaystyle (a,b,c,d)=(2,4,4,6)}
(
a
,
b
,
c
,
d
)
=
(
3
,
6
,
6
,
9
)
{\displaystyle (a,b,c,d)=(3,6,6,9)}
(
a
,
b
,
c
,
d
)
=
(
4
,
8
,
8
,
12
)
{\displaystyle (a,b,c,d)=(4,8,8,12)}
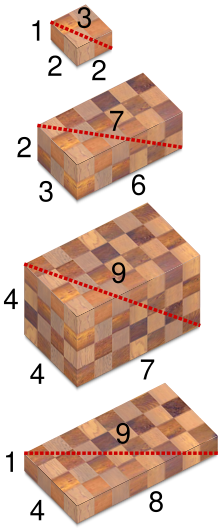
Geometrische Deutung
Bearbeiten
Eigenschaften von pythagoreischen Quadrupeln
Bearbeiten
Das pythagoreische Quadrupel mit dem kleinsten Produkt ist
(
1
,
2
,
2
,
3
)
{\displaystyle (1,2,2,3)}
Sei
a
2
+
b
2
+
c
2
=
d
2
{\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}
a
,
b
,
c
,
d
∈
N
{\displaystyle a,b,c,d\in \mathbb {N} }
[4] Das Produkt
a
b
c
d
{\displaystyle abcd}
12
{\displaystyle 12}
Eine größere Zahl, die dieses Produkt teilt, gibt es nicht, denn für das kleinste pythagoreische Quadrupel (also für
(
a
,
b
,
c
,
d
)
=
(
1
,
2
,
2
,
3
)
{\displaystyle (a,b,c,d)=(1,2,2,3)}
1
⋅
2
⋅
2
⋅
3
=
12
{\displaystyle 1\cdot 2\cdot 2\cdot 3=12}
Erzeugung von pythagoreischen Quadrupeln
Bearbeiten
Seien
(
m
,
n
,
p
,
q
)
{\displaystyle (m,n,p,q)}
a
{\displaystyle a}
a
=
m
2
+
n
2
−
p
2
−
q
2
,
b
=
2
(
m
q
+
n
p
)
,
c
=
2
(
n
q
−
m
p
)
,
d
=
m
2
+
n
2
+
p
2
+
q
2
{\displaystyle {\begin{aligned}a&=m^{2}+n^{2}-p^{2}-q^{2},\\b&=2(mq+np),\\c&=2(nq-mp),\\d&=m^{2}+n^{2}+p^{2}+q^{2}\end{aligned}}}
Gelten zusätzlich die folgenden elf Bedingungen, dann kann damit die Menge von primitiven pythagoreischen Quadrupeln mit ungeradem
a
{\displaystyle a}
[6]
n
q
>
m
p
,
m
2
+
n
2
>
p
2
+
q
2
,
m
≥
0
,
n
≥
1
,
p
≥
0
,
q
≥
1
,
m
+
p
≥
1
,
m
+
n
+
p
+
q
≡
1
(
mod
2
)
,
das heißt,
m
+
n
+
p
+
q
ist ungerade (also muss ein Wert oder müssen drei Werte gerade Zahlen sein)
g
g
T
(
m
2
+
n
2
,
p
2
+
q
2
,
m
q
+
n
p
)
=
1
,
m
=
0
⟹
q
≤
p
,
p
=
0
⟹
n
≤
m
{\displaystyle {\begin{array}{lll}nq>mp,&&m^{2}+n^{2}>p^{2}+q^{2},\\m\geq 0,\;n\geq 1,\;p\geq 0,\;q\geq 1,&&m+p\geq 1,\\m+n+p+q\equiv 1{\pmod {2}},&&{\text{ das heißt, }}m+n+p+q{\text{ ist ungerade (also muss ein Wert oder müssen drei Werte gerade Zahlen sein)}}\\ggT(m^{2}+n^{2},p^{2}+q^{2},mq+np)=1,&&\\m=0\;\Longrightarrow \;q\leq p,&&p=0\;\Longrightarrow \;n\leq m\end{array}}}
Alle primitiven pythagoreischen Quadrupel erfüllen somit die diophantische Gleichung
d
2
=
a
2
+
b
2
+
c
2
{\displaystyle d^{2}=a^{2}+b^{2}+c^{2}}
Lebesguesche Identität nennt:[7] [8]
(
m
2
+
n
2
+
p
2
+
q
2
)
2
=
(
m
2
+
n
2
−
p
2
−
q
2
)
2
+
(
2
m
q
+
2
n
p
)
2
+
(
2
n
q
−
2
m
p
)
2
{\displaystyle (m^{2}+n^{2}+p^{2}+q^{2})^{2}=(m^{2}+n^{2}-p^{2}-q^{2})^{2}+(2mq+2np)^{2}+(2nq-2mp)^{2}}
Beispiel 1:
Sei
m
:=
1
,
n
:=
7
,
p
:=
2
{\displaystyle m:=1,n:=7,p:=2}
q
:=
5
{\displaystyle q:=5}
a
=
21
,
b
=
38
,
c
=
66
{\displaystyle a=21,b=38,c=66}
d
=
79
{\displaystyle d=79}
a
2
+
b
2
+
c
2
=
21
2
+
38
2
+
66
2
=
79
2
=
d
2
(
=
6241
)
{\displaystyle a^{2}+b^{2}+c^{2}=21^{2}+38^{2}+66^{2}=79^{2}=d^{2}\quad (=6241)}
Beispiel 2:
Sei
m
:=
2
,
n
:=
3
,
p
:=
5
{\displaystyle m:=2,n:=3,p:=5}
q
:=
9
{\displaystyle q:=9}
m
2
+
n
2
=
13
>
!
106
=
p
2
+
q
2
{\displaystyle m^{2}+n^{2}=13{\stackrel {!}{>}}106=p^{2}+q^{2}}
a
=
−
93
,
b
=
66
,
c
=
34
{\displaystyle a=-93,b=66,c=34}
d
=
119
{\displaystyle d=119}
a
2
+
b
2
+
c
2
=
(
−
93
)
2
+
66
2
+
34
2
=
119
2
=
d
2
(
=
14161
)
{\displaystyle a^{2}+b^{2}+c^{2}=(-93)^{2}+66^{2}+34^{2}=119^{2}=d^{2}\quad (=14161)}
a
=
−
93
<
0
{\displaystyle a=-93<0}
Beispiel 3:
Sei
m
:=
1
,
n
:=
3
,
p
:=
1
{\displaystyle m:=1,n:=3,p:=1}
q
:=
2
{\displaystyle q:=2}
a
=
5
,
b
=
10
,
c
=
10
{\displaystyle a=5,b=10,c=10}
d
=
15
{\displaystyle d=15}
a
2
+
b
2
+
c
2
=
5
2
+
10
2
+
10
2
=
15
2
=
d
2
(
=
225
)
{\displaystyle a^{2}+b^{2}+c^{2}=5^{2}+10^{2}+10^{2}=15^{2}=d^{2}\quad (=225)}
ggT
(
a
,
b
,
c
,
d
)
=
5
≠
1
{\displaystyle \operatorname {ggT} (a,b,c,d)=5\not =1}
ggT
(
m
2
+
n
2
,
p
2
+
q
2
,
m
q
+
n
p
)
=
5
≠
1
{\displaystyle \operatorname {ggT} (m^{2}+n^{2},p^{2}+q^{2},mq+np)=5\not =1}
Alle pythagoreischen Quadrupel (inklusive der nicht-primitiven) können wie folgt aus zwei positiven ganzen Zahlen
a
{\displaystyle a}
b
{\displaystyle b}
Sei die Parität von
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
b
{\displaystyle b}
p
{\displaystyle p}
a
2
+
b
2
{\displaystyle a^{2}+b^{2}}
p
2
<
a
2
+
b
2
{\displaystyle p^{2}<a^{2}+b^{2}}
c
=
a
2
+
b
2
−
p
2
2
p
{\displaystyle c={\frac {a^{2}+b^{2}-p^{2}}{2p}}}
d
=
a
2
+
b
2
+
p
2
2
p
{\displaystyle d={\frac {a^{2}+b^{2}+p^{2}}{2p}}}
p
=
d
−
c
{\displaystyle p=d-c}
Beispiel:
Sei
a
:=
2
,
b
:=
11
{\displaystyle a:=2,b:=11}
p
:=
5
{\displaystyle p:=5}
c
=
10
{\displaystyle c=10}
d
=
15
{\displaystyle d=15}
p
=
d
−
c
{\displaystyle p=d-c}
a
2
+
b
2
+
c
2
=
2
2
+
11
2
+
10
2
=
15
2
=
d
2
(
=
225
)
{\displaystyle a^{2}+b^{2}+c^{2}=2^{2}+11^{2}+10^{2}=15^{2}=d^{2}\quad (=225)}
Seien
a
=
2
l
{\displaystyle a=2l}
b
=
2
m
{\displaystyle b=2m}
n
{\displaystyle n}
l
2
+
m
2
{\displaystyle l^{2}+m^{2}}
n
2
<
l
2
+
m
2
{\displaystyle n^{2}<l^{2}+m^{2}}
c
=
l
2
+
m
2
−
n
2
n
{\displaystyle c={\frac {l^{2}+m^{2}-n^{2}}{n}}}
d
=
l
2
+
m
2
+
n
2
n
{\displaystyle d={\frac {l^{2}+m^{2}+n^{2}}{n}}}
Diese Methode erzeugt alle pythagoreischen Quadrupel exakt ein Mal, wenn
l
{\displaystyle l}
m
{\displaystyle m}
n
{\displaystyle n}
Beispiel:
Sei
a
:=
14
,
b
:=
6
{\displaystyle a:=14,b:=6}
n
:=
2
{\displaystyle n:=2}
l
=
7
{\displaystyle l=7}
m
=
3
{\displaystyle m=3}
c
=
27
{\displaystyle c=27}
d
=
31
{\displaystyle d=31}
a
2
+
b
2
+
c
2
=
14
2
+
6
2
+
27
2
=
31
2
=
d
2
(
=
961
)
{\displaystyle a^{2}+b^{2}+c^{2}=14^{2}+6^{2}+27^{2}=31^{2}=d^{2}\quad (=961)}
Es gibt kein pythagoreisches Quadrupel, bei dem mehr als eine der Zahlen
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
Sei
n
{\displaystyle n}
a
=
n
,
b
=
n
+
1
,
c
=
a
b
,
d
=
c
+
1
{\displaystyle {\begin{aligned}a&=n,\\b&=n+1,\\c&=ab,\\d&=c+1\end{aligned}}}
Beispiel:
Sei
n
=
a
=
3
{\displaystyle n=a=3}
b
=
4
{\displaystyle b=4}
c
=
12
{\displaystyle c=12}
d
=
13
{\displaystyle d=13}
a
2
+
b
2
+
c
2
=
3
2
+
4
2
+
12
2
=
13
2
=
d
2
(
=
169
)
{\displaystyle a^{2}+b^{2}+c^{2}=3^{2}+4^{2}+12^{2}=13^{2}=d^{2}\quad (=169)}
Seien
x
,
y
,
z
{\displaystyle x,y,z}
(
a
,
b
,
c
,
d
)
{\displaystyle (a,b,c,d)}
a
=
x
2
−
y
2
−
z
2
,
b
=
2
x
y
,
c
=
2
x
z
,
d
=
x
2
+
y
2
+
z
2
{\displaystyle {\begin{aligned}a&=x^{2}-y^{2}-z^{2},\\b&=2xy,\\c&=2xz,\\d&=x^{2}+y^{2}+z^{2}\end{aligned}}}
Beispiel:
Sei
x
=
2
{\displaystyle x=2}
y
=
1
{\displaystyle y=1}
z
=
1
{\displaystyle z=1}
So ist
a
=
2
{\displaystyle a=2}
b
=
4
{\displaystyle b=4}
c
=
4
{\displaystyle c=4}
d
=
6
{\displaystyle d=6}
a
2
+
b
2
+
c
2
=
2
2
+
4
2
+
4
2
=
6
2
=
d
2
(
=
36
)
{\displaystyle a^{2}+b^{2}+c^{2}=2^{2}+4^{2}+4^{2}=6^{2}=d^{2}\quad (=36)}
(
1
,
2
,
2
,
3
)
{\displaystyle (1,2,2,3)}
↑ Zur Schreibweise: Im aktuellen Duden – Das große Wörterbuch der deutschen Sprache in zehn Bänden - ISBN 3-411-70360-1 wird das Adjektiv „pythagoreisch“ in dieser Schreibweise gegeben und die Schreibweise „pythagoräisch“ als österreichische Sonderform bezeichnet.
↑ a b Robert Spira : The Diophantine Equation x2 +y2 +z2 =m2 . The American Mathematical Monthly 69 (5), 1962, S. 360–365 , abgerufen am 11. Oktober 2019 . ↑ Raymond A. Beauregard, E. R. Suryanarayan: Pythagorean Boxes. Mathematics Magazine 74 (3), Juni 2001, S. 222–227 , abgerufen am 11. Oktober 2019 . ↑ Des MacHale, Christian van den Bosch: Generalising a result about Pythagorean triples. The Mathematical Gazette 96 (535), März 2012, S. 91–96 , abgerufen am 11. Oktober 2019 . ↑ Paul Oliverio: Self-Generating Pythagorean Quadruples and n -Tuples. S. 98–101 , abgerufen am 18. Oktober 2019 . ↑ Robert Spira: The Diophantine Equation x2 +y2 +z2 =m2 , Theorem 2. The American Mathematical Monthly 69 (5), 1962, S. 362 , abgerufen am 11. Oktober 2019 . ↑ Pythagorean Quadruple. abgerufen am 11. Oktober 2019 . ↑ Eric W. Weisstein : Lebesgue Identity. Wolfram MathWorld , abgerufen am 18. Oktober 2019 . ↑ Titu Andreescu, Dorin Andrica, Ion Cucurezeanu: An Introduction to Diophantine Equations: A Problem-Based Approach, Theorem 2.2.3. S. 79 , abgerufen am 18. Oktober 2019 .