Cauchy-Kriterium

Das (Bolzano-)Cauchy-Kriterium (auch: Konvergenzprinzip, [allgemeines] Kriterium von Bolzano-Cauchy oder Konvergenzkriterium von Bolzano-Cauchy) ist ein mathematisches Konvergenzkriterium für Folgen und Reihen und von fundamentaler Bedeutung für die Analysis. Mit ihm kann entschieden werden, ob eine Folge oder Reihe reeller oder komplexer Zahlen konvergent oder divergent ist. Allgemeiner kann das Cauchy-Kriterium auch auf Folgen von Elementen eines vollständigen metrischen Raums oder auf Reihen von Vektoren eines Banachraums angewandt werden. Es ist nach dem französischen Mathematiker Augustin Louis Cauchy benannt, der dieses Konvergenzkriterium 1821 in seinem Lehrbuch „Cours d’Analyse“ veröffentlichte.

Eine Folge konvergiert, wenn der Abstand der Folgenglieder im Verlauf der Folge beliebig klein wird.

Wenn der Abstand der Folgenglieder im Verlauf der Folge nicht beliebig klein wird, dann divergiert die Folge.

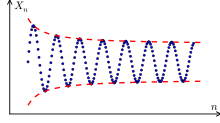
Cauchy-Kriterium für Folgen

Kriterium

Eine Folge $(a_{n})_{n\in \mathbb {N} }=a_{1},a_{2},\ldots$ reeller oder komplexer Zahlen konvergiert gegen einen Grenzwert in den reellen bzw. komplexen Zahlen, wenn es zu jedem $\varepsilon >0$ einen Index $N$ gibt, sodass der Abstand zweier beliebiger Folgenglieder ab diesem Index kleiner als $\varepsilon$ ist. Formal lässt sich die Cauchy-Eigenschaft dadurch beschreiben, dass

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad \left|a_{m}-a_{n}\right|<\varepsilon$

gilt.

Das Cauchy-Kriterium besitzt für die Analysis eine fundamentale Bedeutung. Eine Folge reeller oder komplexer Zahlen konvergiert nämlich genau dann gegen einen Grenzwert, wenn sie eine Cauchy-Folge ist. Diese sogenannte Vollständigkeit der reellen oder komplexen Zahlen ist eine grundlegende Eigenschaft dieser Zahlbereiche.

Das Beispiel $a_{n}=\ln(n)$ zeigt, dass es im Cauchy-Kriterium wirklich auf den Abstand zweier beliebiger Folgenglieder ab dem Index $N$ ankommt und nicht nur auf den Abstand aufeinanderfolgender Folgenglieder.

Beispiel

Die Folge reeller Zahlen $(a_{n})$ sei rekursiv durch

$a_{n+1}={\tfrac {1}{2}}(1-a_{n}^{2})$

gegeben, wobei $a_{0}=0$ ist. Um die Konvergenz dieser Folge mit dem Cauchy-Kriterium zu zeigen, berechnet man zunächst

$|a_{n+1}-a_{n}|=|{\tfrac {1}{2}}(1-a_{n}^{2})-{\tfrac {1}{2}}(1-a_{n-1}^{2})|={\tfrac {1}{2}}|a_{n}^{2}-a_{n-1}^{2}|={\tfrac {1}{2}}|a_{n}+a_{n-1}|\,|a_{n}-a_{n-1}|\leq {\tfrac {1}{2}}|a_{n}-a_{n-1}|$,

wobei die letzte Abschätzung aus der Dreiecksungleichung

$|a_{n}+a_{n-1}|\leq |a_{n}|+|a_{n-1}|\leq 1$

folgt, da die einzelnen Folgenglieder durch ${\tfrac {1}{2}}$ beschränkt sind. Wendet man die Ungleichung $n$-mal an, erhält man mit $q={\tfrac {1}{2}}$

$|a_{n+1}-a_{n}|\leq q^{n}|a_{1}-a_{0}|=q^{n+1}$.

Allgemein gilt nun für $m>n$

$|a_{m}-a_{m-1}|\leq q|a_{m-1}-a_{m-2}|\leq \cdots \leq q^{m-n-1}|a_{n+1}-a_{n}|$

und durch wiederholte Anwendung der Dreiecksungleichung sowie der geometrischen Summenformel

$|a_{m}-a_{n}|\leq \sum _{i=0}^{m-n-1}q^{i}|a_{n+1}-a_{n}|\leq {\frac {1-q^{m-n}}{1-q}}q^{n+1}\leq {\frac {1}{1-q}}q^{n+1}=2q^{n+1}=q^{n}<\varepsilon$

für alle $n,m>N={\tfrac {\ln \varepsilon }{\ln q}}$. Damit ist die Folge $(a_{n})$ eine Cauchy-Folge und somit konvergent.

Beweis

Der Beweis des Cauchy-Kriteriums kann mit dem Satz von Bolzano-Weierstraß als Axiom für die Vollständigkeit der reellen oder komplexen Zahlen erfolgen. Ist $(a_{n})$ eine Cauchy-Folge, dann kann man zu $\varepsilon =1$ einen Index $N\in \mathbb {N}$ finden, sodass

$|a_{n}|=|a_{n}-a_{N}+a_{N}|\leq |a_{n}-a_{N}|+|a_{N}|\leq 1+|a_{N}|$

für alle $n\geq N$ ist. Also ist die Cauchy-Folge durch

$\max\{|a_{1}|,|a_{2}|,\ldots ,|a_{N-1}|,1+|a_{N}|\}$

beschränkt. Der Satz von Bolzano-Weierstraß besagt nun, dass die Folge $(a_{n})$ einen Häufungspunkt $a$ besitzt. Bezeichnet $(a_{n_{i}})_{i\in \mathbb {N} }$ eine Teilfolge, die gegen $a$ konvergiert, ergibt sich mit

$|a_{n}-a|\leq |a_{n}-a_{n_{i}}|+|a_{n_{i}}-a|$,

dass $a$ der Grenzwert der gesamten Folge sein muss.

Verallgemeinerung

Allgemeiner kann das Cauchy-Kriterium auch zur Untersuchung der Konvergenz von Folgen von Elementen eines vollständigen metrischen Raums $(X,d)$ verwendet werden. Eine Folge $(x_{i})_{i\in \mathbb {N} }$ von Elementen $x_{i}\in X$ konvergiert genau dann gegen einen Grenzwert in der Menge $X$, wenn

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad d(x_{m},x_{n})<\varepsilon$

gilt, wenn sie also eine Cauchy-Folge bezüglich der Metrik $d$ ist. In einem nicht vollständigen metrischen Raum bildet das Cauchy-Kriterium nur eine notwendige Bedingung für die Konvergenz einer Folge, das heißt: ist eine gegebene Folge keine Cauchy-Folge, so divergiert sie.

Cauchy-Kriterium für Reihen

Kriterium

Eine Reihe

$\sum _{i=1}^{\infty }a_{i}=a_{1}+a_{2}+\ldots$

mit reellen oder komplexen Summanden $a_{i}$ konvergiert genau dann gegen einen Grenzwert in den reellen bzw. komplexen Zahlen, wenn

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m>n\geq N\colon \quad |a_{n+1}+a_{n+2}+\ldots +a_{m}|<\varepsilon$

gilt.

Beispiele

Die Reihe $1+{\tfrac {1}{4}}+{\tfrac {1}{9}}+{\tfrac {1}{16}}+\ldots$ konvergiert, da

$\left|\sum _{i=n+1}^{m}{\frac {1}{i^{2}}}\right|<\left|\sum _{i=n+1}^{m}{\frac {1}{i(i-1)}}\right|=\left|\sum _{i=n+1}^{m}\left({\frac {1}{i-1}}-{\frac {1}{i}}\right)\right|={\frac {1}{n}}-{\frac {1}{m}}<{\frac {1}{n}}\leq {\frac {1}{N}}<\varepsilon$,

wenn $N>{\tfrac {1}{\varepsilon }}$ gewählt wird, was aufgrund des archimedischen Axioms immer möglich ist.

Hingegen divergiert die harmonische Reihe $1+{\tfrac {1}{2}}+{\tfrac {1}{3}}+{\tfrac {1}{4}}+\ldots$, denn wählt man $\varepsilon ={\tfrac {1}{2}}$, $N$ beliebig, $n\geq N$ und $m=2n$, dann gilt immer

$\left|\sum _{i=n+1}^{m}{\frac {1}{i}}\right|=\left|{\frac {1}{n+1}}+\ldots +{\frac {1}{2n}}\right|\geq n\cdot {\frac {1}{2n}}={\frac {1}{2}}\geq \varepsilon$.

Beweis

Es ist nachzuweisen, dass die Folge $(s_{n})$ der Partialsummen

$s_{n}=\sum _{i=1}^{n}a_{i}$

konvergiert. Nach dem Cauchy-Kriterium für Folgen muss also für jedes $\varepsilon >0$ ein Index $N$ so existieren, dass für Indizes $m,n\geq N$ die Ungleichung $|s_{m}-s_{n}|<\varepsilon$ gilt. Ohne Beschränkung der Allgemeinheit kann man hierbei $m>n$ annehmen. Nach Voraussetzung gilt dann

$|s_{m}-s_{n}|=|(a_{1}+\ldots +a_{m})-(a_{1}+\ldots +a_{n})|=|a_{n+1}+\ldots +a_{m}|<\varepsilon$

und somit konvergiert die Partialsummenfolge gegen einen Grenzwert und damit die gesamte Reihe.

Verallgemeinerung

Allgemeiner lässt sich das Cauchy-Kriterium auch für Reihen von Vektoren aus einem vollständigen normierten Raum $(V,\|\cdot \|)$ fassen. Eine Reihe von Vektoren $v_{i}\in V$

$\sum _{i=1}^{\infty }v_{i}$

konvergiert genau dann gegen einen Grenzwert in dem Vektorraum $V$, wenn

$\forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m>n\geq N\colon \quad \|v_{n+1}+v_{n+2}+\ldots +v_{m}\|<\varepsilon$

gilt, wobei $\|\cdot \|$ die Norm des Banachraums ist.

Siehe auch

• Monotoniekriterium

Literatur

• Konrad Königsberger: Analysis 1. Springer-Verlag, Berlin u. a. 2004, ISBN 3-540-41282-4.
• Otto Forster: Analysis Band 1: Differential- und Integralrechnung einer Veränderlichen. 8. Auflage. Vieweg-Verlag, 2006, ISBN 3-528-67224-2.

Weblinks

Wikibooks: Mathe für Nicht-Freaks: Cauchy-Folgen und das Cauchy-Kriterium – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Cauchy-Kriterium für Reihen – Lern- und Lehrmaterialien

• L.D. Kudryavtsev: Cauchy criteria. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org). 
• Cauchy Criterion for Convergence. In: PlanetMath. (englisch)
• Eric W. Weisstein: Cauchy Criterion. In: MathWorld (englisch).