Silberner Schnitt

Der Silberne Schnitt (angelehnt an die Bezeichnung Goldener Schnitt) ist das Teilungsverhältnis einer Strecke (Länge) oder anderen Größe (Bereich), bei dem das Verhältnis der Summe des verdoppelten größeren und des kleineren Teils zum größeren Teil gleich dem Verhältnis des größeren zum kleineren Teil ist. Dieses Teilungsverhältnis erhält man z. B. bei einer Konstruktion mit Zirkel und Lineal mithilfe eines halben Achtecks.

Silberner Schnitt

Definition und Eigenschaften

Silberner Schnitt, Proportionen der Streckenteile:
$\delta _{S}={\frac {a}{b}}={\frac {2a+b}{a}}$

Mit $a$ als größerem und $b$ als kleinerem Teil sowie $\delta _{S}$ als Silbernem Schnitt gilt:

${\frac {2a+b}{a}}={\frac {a}{b}}=:\delta _{S}$

Der Silberne Schnitt $\delta _{S}$ erfüllt daher die Gleichung

$\delta _{S}={\frac {1}{\delta _{S}}}+2$

oder umgeformt ergibt die quadratische Gleichung

$\delta _{S}^{2}-2\delta _{S}-1=0$.

Wegen $\delta _{S}>1$ folgt daraus

$\delta _{S}=1+{\sqrt {2}}=2{,}414213\ldots$.

Goldener und Silberner Schnitt lassen sich durch die Funktion

$f(x)={\frac {x}{2}}+{\sqrt {\left({\frac {x}{2}}\right)^{2}+1}}$

darstellen, wobei der Goldene Schnitt Funktionswert für $x=1$, der Silberne Schnitt für $x=2$ ist.

Der Silberne Schnitt lässt sich auch durch trigonometrische Funktionen ausdrücken und ist mit dem Winkel $\pi /8=22{,}5^{\circ }$ verbunden:

$\delta _{S}=\cot {\frac {1}{8}}\pi$

$\delta _{S}=\tan {\frac {3}{8}}\pi$

Zudem besitzt der Silberne Schnitt ähnlich wie der Goldene Schnitt eine besonders einfache Darstellung als Kettenbruch:

$\delta _{S}=[2;2,2,2,\dotsc ]=2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\dotsb }}}}}}$

Konstruktion

Ausgangssituation

Silberner Schnitt in einem halben regelmäßigen Achteck nach dem Satz von Pythagoras:
${\overline {AB}}\;{\widehat {=}}\;{\sqrt {2}}=a+b$
${\overline {IJ}}\;{\widehat {=}}\;1+{\sqrt {2}}-1+1=1+{\sqrt {2}}=\delta _{S}$

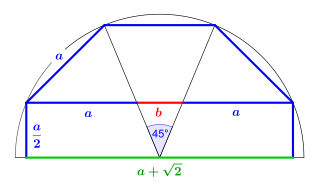
Ausgehend vom regelmäßigen Achteck mit einer Seitenlänge $b_{0}=1$ soll die folgende Beschreibung zur nebenstehenden Konstruktion die Teilung einer Strecke im Verhältnis des Silbernen Schnittes verdeutlichen.

• Die geometrische Herleitung des Zahlenwertes $1+{\sqrt {2}}$ von $\delta _{S}$ mit Zirkel und Lineal entsteht im Verlauf der Konstruktion. Sie erweist sich als praktikable Alternative zur rechnerischen Herleitung.

Zuerst wird nach dem Errichten einer Senkrechten auf eine Gerade, jeweils ab dem Punkt $A$, um dem Punkt $A$ ein Viertelkreis mit dem Radius $r=1$ gezeichnet, damit ergeben sich die Punkte $C$ und $D$. Halbiert man nun den rechten Winkel $CAD$, ergeben sich der Winkel $45^{\circ }$, der Schnittpunkt $E$ und somit als Strecke ${\overline {AE}},$ die erste Seite des halben Achtecks. Es folgt ein Kreisbogen mit dem Radius ${\overline {AE}}$ um den Punkt $E$ und eine Parallele zur Strecke ${\overline {AC}}$ ab $E$; beide schneiden sich in $F$ und bilden somit als Strecke ${\overline {EF}}$ die zweite Seite des halben Achtecks. Um den Mittelpunkt $M$ des halben Achtecks zu erhalten, konstruiert man die zwei Mittelsenkrechten $Ms_{1}$ und $Ms_{2}$ der beiden Achteckseiten. Anschließend werden durch den Mittelpunkt $M$ die Mittelachse parallel zur Strecke ${\overline {AC}}$ und um $M$ der Halbkreis mit dem Radius ${\overline {AM}}$ gezeichnet. Es ergibt sich der Schnittpunkt $H$ und somit als Strecke ${\overline {FH}}$ die dritte Seite des halben Achtecks. Die Verbindungen der Punkte $E$ und $F$ mit dem Mittelpunkt $M$ ergeben den Schnittpunkt $B$ sowie den Zentriwinkel $45^{\circ }$ der Achteckseite. Um das halbe Achteck fertigzustellen, bedarf es noch zweier Senkrechten zur Strecke ${\overline {AH}}$, jeweils ab den Punkten $A$ und $H$ bis auf die Mittelachse. Dabei ergeben sich schließlich die beiden Schnittpunkte $I$ und $J$.

Die Seite ${\overline {EM}}$ des Dreiecks $MFE$ schneidet die Strecke ${\overline {AB}}$, deren Länge ${\sqrt {2}}$ entspricht, im Punkt $C$ und teilt sie dort im Verhältnis des Silbernen Schnittes.

Das Ergebnis zeigt, dass jede der beiden Strecken ${\overline {AH}}$ und ${\overline {IJ}}$ die Länge $1+{\sqrt {2}}-1+1=1+{\sqrt {2}}$ hat.

Setzt man in die allgemeinen Formel für $\delta _{S}={\frac {a}{b}}={\frac {a_{0}}{b_{0}}}$ ergibt sich

${\overline {IJ}}={\frac {a_{0}}{b_{0}}}={\frac {1+{\sqrt {2}}}{1}}=1+{\sqrt {2}},$ daraus folgt

${\overline {IJ}}=\delta _{S}=1+{\sqrt {2}}\approx 2{,}414\,213\,562.$

• In Worten, die Länge der Strecke ${\overline {IJ}}$ entspricht dem Zahlenwert $\approx 2{,}414\,213\,562.$

Innere Teilung

Silberner Schnitt, innere Teilung
${\frac {a}{b}}=1+{\sqrt {2}}=\delta _{S}$

Für die innere Teilung der Strecke ${\overline {AB}}$ im Verhältnis des Silbernen Schnittes sind aus der Zeichnung des halben regelmäßigen Achtecks prinzipiell folgende Konstruktionselemente ableitbar:

• Grünes Dreieck $ACE$
• Mittelpunkt $G$ der Strecke ${\overline {AB}}$
• Kreisbogen $CED$ um $A$, erzeugt Teilungspunkt $C$

Zu Beginn wird die Strecke ${\overline {AB}}$ halbiert, es ergibt sich der Mittelpunkt $G$. Anschließend zieht man den Halbkreis mit dem Radius ${\overline {GA}}$ um den Punkt $G$. Es folgt eine Senkrechte auf die Strecke ${\overline {AB}}$ durch den Punkt $G$, dabei ergibt sich der Schnittpunkt $E$ mit dem Halbkreis. Der abschließende Kreisbogen um den Punkt $A$ mit dem Radius ${\overline {AE}}$ teilt in $C$ die Strecke ${\overline {AB}}$ im Verhältnis des Silbernen Schnittes mit $a$ als größerem und $b$ als kleinerem Teil.

Äußere Teilung

Silberner Schnitt, äußere Teilung
${\frac {a}{b}}=1+{\sqrt {2}}=\delta _{S}$

Ähnlich wie der Goldene Schnitt ist auch der Silberne Schnitt mit einer äußeren Teilung, durch eine Verlängerung der vorgegebenen Strecke, konstruierbar.

Für die äußere Teilung der Strecke ${\overline {AB}}$ im Verhältnis des Silbernen Schnittes sind aus der Zeichnung des halben regelmäßigen Achtecks prinzipiell folgende Konstruktionselemente ableitbar:

• Grünes Dreieck $ACE$
• Kreisbogen $CED$ um $A$
• Kreisbogen $ABF$ um $E$, erzeugt die Strecke ${\overline {AB}}$

Es beginnt mit der Konstruktion eines rechten Winkels (einer Senkrechten) auf der vorgegebenen Strecke ${\overline {AC}}$ im Punkt $A$. Anschließend wird um den Punkt $A$, ab dem Punkt $C$, ein Viertelkreis bis zur Senkrechten gezeichnet, es ergibt sich der Schnittpunkt $D$. Nun folgt die Halbierung des rechten Winkels $CAD$, dabei ergeben sich der Winkel $45^{\circ }$ und der Schnittpunkt $E$. Weiter geht es mit der Verlängerung der Strecke ${\overline {AC}}$ ab dem Punkt $C$ um etwa die Hälfte der Strecke ${\overline {AC}}$. Der abschließende Kreisbogen um den Punkt $E$ mit dem Radius ${\overline {AE}}$ verlängert die vorgegebene Strecke ${\overline {AC}}$ in $B$ um die Länge der Strecke ${\overline {CB}}$. Somit ist die Strecke ${\overline {AB}}$ geteilt im Verhältnis des Silbernen Schnittes mit $a$ als größerem und $b$ als kleinerem Teil.

Silbernes Rechteck

Bild 1
Silbernes Rechteck, anhand des Silbernen Schnittes mit innerer Teilung
${\frac {a}{b}}={\frac {a_{1}}{b_{1}}}=1+{\sqrt {2}}=\delta _{S}$

Ein Rechteck mit den Seitenlängen $a$ und $b<a$ heißt Silbernes Rechteck, wenn der Quotient der Seitenlängen gerade der Silberne Schnitt ist:

${\frac {a}{b}}={\frac {1}{{\sqrt {2}}-1}}=1+{\sqrt {2}}=\delta _{S}$

Das Silberne Rechteck kann mit Zirkel und Lineal konstruiert werden.

Um die beiden Seitenlängen $a$ und $b$ zu finden, wird zunächst eine beliebige Strecke ${\overline {AB}}$ im Verhältnis des Silbernen Schnittes mit einem der beiden oben beschriebenen Verfahren (innere Teilung oder äußere Teilung) geteilt. Die damit ermittelte Seite $b$ wird nun in die Senkrechte hochgeklappt und anschließend das Silberne Rechteck fertiggestellt.

Die nebenstehende Darstellung (Bild 1) zeigt, der Mittelpunkt $G$ der Strecke ${\overline {AB}}$ teilt jetzt die Seitenlänge $a$ im Verhältnis des Silbernen Schnittes. Es entstehen dadurch die Seitenlängen $a_{1}$ und $b_{1}$ eines weiteren Silbernen Rechtecks, was mit der Konstruktion neuer „Silberner“ Paare $(a_{2},b_{2}),\ (a_{3},b_{3}),\dotsc$ natürlich beliebig weit fortgesetzt werden kann.

Eine weitere – sehr einfache – Möglichkeit ein Silbernes Rechteck mithilfe einer alternativen äußeren Teilung darzustellen, zeigt das nebenstehende Bild 2.

Bild 2
Silbernes Rechteck, Basis ist ein Quadrat

Ausgehend von einem Quadrat $ABCD$ mit der beliebigen Seitenlänge $a,$ wird z. B. die Strecke ${\overline {DA}}$ über $A$ hinaus verlängert und ein Kreisbogen mit dem Radius ${\overline {DB}}=a\cdot {\sqrt {2}}$ gezogen, bis dieser die Verlängerung in $E$ schneidet. Die somit erzeugte Strecke ${\overline {AE}}$ entspricht der gesuchten Seite $b$ des Silbernen Rechtecks, denn es gilt:

$\delta _{S}={\frac {a}{b}},$

nach dem Umformen ist

$b={\frac {a}{\delta _{S}}}$

daraus folgt:

$b={\frac {a}{1+{\sqrt {2}}}}=a\cdot {\sqrt {2}}-a$

Anders als beim Goldenen Schnitt und beim Goldenen Rechteck gibt es nur eher wenige Beispiele aus dem Alltag, wo man diesen Quotienten beobachten kann. So gibt es beispielsweise Autos, deren Länge und Breite dem Silbernen Schnitt entsprechen. Eine einfache Möglichkeit, ein Silbernes Rechteck selbst zu erstellen, ist mithilfe eines DIN-A4-Blattes. Dieses hat ein Seitenverhältnis von $1:{\sqrt {2}}$. Durch Knicken und Schneiden kann man so ein Silbernes Rechteck konstruieren.

Literatur

• Donald B. Coleman: The Silver Ratio: A Vehicle for Generalization. In: The Mathematics Teacher, Vol. 82, No. 1 (Januar 1989), S. 54–59 (JSTOR:27966097).

Weblinks

• An Introduction to Continued Fractions. The Silver Means.
• Continued Fractions and the Fibonacci Numbers.
• Der silberne Schnitt. Faltung eines silbernen Vierecks.
• Numberphile: The Silver Ratio auf YouTube, 11. Mai 2018, abgerufen am 19. Januar 2019.