Scherung (Geometrie)

Unter einer Scherung oder auch Transvektion versteht man ursprünglich in der Geometrie der Ebene bestimmte affine Abbildungen der Ebene auf sich selbst, bei denen der Flächeninhalt erhalten bleibt. Bei einer Scherung bleibt eine Gerade der Ebene (die Fixpunktgerade oder Achse der Scherung) fix, das heißt, jeder Punkt dieser Geraden wird auf sich abgebildet. Alle anderen Punkte der Ebene werden parallel zur Achse verschoben, dabei ist die Länge des Verschiebungsvektors eines Punktes proportional zum Abstand dieses Punktes von der Achse. Alle Geraden, die parallel zur Achse sind, werden auf sich abgebildet, sind also Fixgeraden. Strecken auf diesen Geraden werden längentreu abgebildet.

Eine Scherung bildet ein Rechteck auf ein Parallelogramm ab

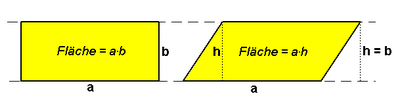
Bei einer Scherung bleibt also der Abstand jedes Punktes zur Achse unverändert. Damit werden Rechtecke und Dreiecke, bei denen eine Seite parallel zur Achse ist, auf Parallelogramme bzw. Dreiecke abgebildet, die (lotrecht zu der Seite, die parallel zur Achse ist) eine gleich lange Höhe haben (vgl. die Abbildung).

Der Begriff der (ebenen) Scherung kann unterschiedlich auf Affinitäten im Raum und in höheren Dimensionen verallgemeinert werden. Zwei Möglichkeiten, bei denen die verallgemeinerte Scherung das Volumen der abgebildeten Figuren nicht ändert, werden hier dargestellt.

Die Hintereinanderausführung einer Scherung und einer zentrischen Streckung (in beliebiger Reihenfolge) ergibt eine Scherstreckung, bei der im Allgemeinen Flächen- und Rauminhalte nicht gleich bleiben.

Scherungen in der Ebene

Eine Affinität $\sigma$ eines zweidimensionalen affinen Raumes $E$ (der "Ebene") ist genau dann eine Scherung, wenn

1. es zwei verschiedene Fixpunkte $F_{1}$ und $F_{2}$ gibt, formal:

   $\exists F_{1},F_{2}\in E\colon F_{1}\neq F_{2}\land F_{1}^{\sigma }=F_{1}\land F_{2}^{\sigma }=F_{2}$

2. und einen beliebigen Punkt $P$, der nicht auf der Verbindungsgeraden $a$ der zwei Fixpunkte aus (1) liegt, unter $\sigma$ Fixpunkt ist oder parallel zu $a$ verschoben wird. formal:

   $\exists P\in E,P\not \in F_{1}F_{2}\land (P^{\sigma }=P\lor PP^{\sigma }{\mathbin {||}}F_{1}F_{2})$.

Aus der ersten Bedingung folgt mit den Eigenschaften einer Affinität, dass die Verbindungsgerade der beiden Fixpunkte eine Fixpunktgerade (Achse $a$) ist. Die zweite Bedingung lässt (mit der Möglichkeit eines dritten Fixpunktes außerhalb von $a$) auch die identische Abbildung als Scherung zu oder erzwingt, dass mit einem Punkt außerhalb der Fixpunktgeraden alle Punkte außerhalb von $a$ parallel zu $a$ verschoben werden.

Allgemein ist eine Affinität in der Ebene eindeutig bestimmt, wenn zu drei Punkten, die nicht auf einer Geraden liegen, jeweils die nicht auf einer Geraden liegenden Bildpunkte angegeben werden.

Eigenschaften

Aus zwei Schrägspiegelungen resultierende Scherung

Bemerkenswert ist, dass zur Charakterisierung einer Scherung keine Abstands- oder Flächeninhaltsbegriffe benutzt werden müssen. Scherungen lassen sich so in jeder affinen Ebene definieren. Die in der Einleitung genannten Eigenschaften sind dann so zu präzisieren:

Ist in der Ebene ein euklidischer Abstand und ein mit diesem Abstand verträglicher Flächeninhalt definiert, dann bleiben bei einer Scherung mit Achse $a$

• der Abstand zwischen zwei Punkten, die auf $a$ oder Parallelen zu $a$ liegen,
• der Abstand zwischen zwei zu $a$ parallelen Geraden und
• der (orientierte) Flächeninhalt jeder messbaren Fläche

erhalten.

In der reellen Ebene kann man durch Wahl einer "Einheitsellipse" oder gleichwertig durch Wahl eines affinen Koordinatensystems als Orthonormalbasis unterschiedliche euklidische Strukturen, d. h. unterschiedliche Winkel- und Abstandsbegriffe einführen. Eine Scherung hat nun die genannten Invarianzeigenschaften in Bezug auf jede dieser Strukturen, während zum Beispiel eine Drehung bezüglich einer euklidischen Struktur bezüglich einer anderen keine Drehung zu sein braucht. Diese Unabhängigkeit von der euklidischen Struktur teilen die Scherungen mit den Parallelverschiebungen.

Eine weitere Eigenschaft der Scherung besteht darin, dass sie als Verkettung zweier verschiedener Schrägspiegelungen an derselben Geraden g darstellbar ist.

Bildkonstruktion

Konstruktion eines Bildpunktes $Q'$ von $Q$ unter einer Scherung, bei der die Achse $a$ und ein Punkt $P$ samt Bildpunkt $P'$ außerhalb der Achse gegeben sind.

Eine Scherung in der Ebene ist festgelegt, wenn ihre Achse $a$ und für einen gegebenen Punkt $P$ außerhalb der Achse sein Bildpunkt $P'$ gegeben sind. Dann kann das Bild eines weiteren Punktes $Q$, der nicht auf der Achse und nicht auf der Verbindungsgeraden $PP'$ liegt, folgendermaßen konstruiert werden, die Abbildung rechts zeigt die Schritte (rot) der Konstruktion:

1. Konstruiere die Parallele $q$ zu $a$ durch $Q$.
2. Zeichne die Verbindungsgerade $PQ$. Sie schneidet die Achse $a$ in einem Fixpunkt $F$.
3. Zeichne die Verbindungsgerade $FP'$. Sie ist das Bild der Gerade $PQ$. Daher ist der Schnittpunkt $Q'$ von $FP'$ mit $q$ der gesuchte Bildpunkt.

Wenn der abzubildende Punkt $Q$ auf der Achse liegt, ist er selbst Fixpunkt. Liegt er auf der Verbindungsgeraden $PP'$, dann muss entweder nach obigem Konstruktionstext zuerst für einen Hilfspunkt $H$ außerhalb von $PP'$ und der Achse der Bildpunkt bestimmt werden, oder man verwendet für die Bildkonstruktion die Tatsache, dass die Scherung auf $PP'$ als Verschiebung operiert.

Matrixdarstellung

Wählt man in der Ebene ein kartesisches Koordinatensystem, bei dem die $x$-Achse mit der Achse der Scherung zusammenfällt, dann wird diese Scherung durch die lineare Abbildung

${\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}x+my\\y\end{pmatrix}}={\begin{pmatrix}1&m\\0&1\end{pmatrix}}\cdot {\begin{pmatrix}x\\y\end{pmatrix}}\quad$

mit der Abbildungsmatrix

${\begin{pmatrix}1&m\\0&1\end{pmatrix}}$

dargestellt. Ist die Achse der Scherung hingegen die $y$-Achse, tauschen $0$ und $m$ in der Abbildungsmatrix ihre Plätze. Beide Abbildungen verändern den Winkel zwischen den Koordinatenachsen jeweils um $\arctan m$.

Ist eine affine Abbildung $\alpha$ der Ebene durch ihre Abbildungsmatrix $M$ und ihre Verschiebung ${\vec {v}}$ gegeben,

${\vec {x}}\mapsto M\cdot {\vec {x}}+{\vec {v}}$,

dann ist $\alpha$ genau dann eine Scherung, wenn

1. die Fixpunktgleichung ${\vec {x_{F}}}=M\cdot {\vec {x_{F}}}+{\vec {v}}$ eine Lösung ${\vec {x_{F}}}$ hat
2. und die Matrix $M$ das charakteristische Polynom $\chi _{M}(X)=(X-1)^{2}$ hat. Dabei ist die Determinante gegeben als

   $\chi _{M}(X):=\det \left({\begin{pmatrix}X&0\\0&X\end{pmatrix}}-M\right)$.

Für algebraische Untersuchungen ist es bequem, die betrachteten affinen Abbildungen als 3×3-Matrizen (erweiterte Abbildungsmatrizen) bezüglich einer festen Basis darzustellen. Das entspricht einer Darstellung der affinen Abbildung in homogenen Koordinaten: Statt

${\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}m_{11}&m_{12}\\m_{21}&m_{22}\end{pmatrix}}\cdot {\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}v_{1}\\v_{2}\end{pmatrix}}$

schreibt man dann

${\begin{pmatrix}x\\y\\1\end{pmatrix}}\mapsto {\begin{pmatrix}m_{11}&m_{12}&v_{1}\\m_{21}&m_{22}&v_{2}\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}x\\y\\1\end{pmatrix}}$.

Algebraische Struktur

Die Verkettung zweier Scherungen ist im Allgemeinen keine Scherung mehr. Die Menge aller Scherungen der Ebene bildet also insbesondere keine Gruppe. Ihre erweiterten Abbildungsmatrizen sind eine Teilmenge der Gruppe der Verschiebungsmatrizen in der Speziellen linearen Gruppe $SL(3,\mathbb {K} )$. Das ist eine Gruppe. (Sie besteht aus den Matrizen der Form

${\begin{pmatrix}m_{11}&m_{12}&v_{1}\\m_{21}&m_{22}&v_{2}\\0&0&1\end{pmatrix}}$,

deren Determinante 1 ist. Genau die erweiterten Abbildungsmatrizen flächentreuer und orientierungs­erhaltender Affinitäten bilden diese Gruppe.)

Die Menge der Scherungen mit einer gemeinsamen Achse bildet eine abelsche Gruppe. Sie ist isomorph zur Gruppe der Verschiebungen in eine feste Richtung, denn man kann ein affines bzw. kartesisches Koordinatensystem wählen (mit der gemeinsamen Achse als $x$-Achse), in der sie alle eine Darstellung der Form

${\begin{pmatrix}1&m&0\\0&1&0\\0&0&1\end{pmatrix}}$

haben. Für die Darstellung der Scherung kommt es auf die Lage des Ursprungs auf der Achse nicht an.

Für Scherungen, deren Achsen parallel sind, kann man ein gemeinsames affines bzw. kartesisches Koordinatensystem wählen, in dem ihre erweiterten Abbildungsmatrizen die Form

${}{\begin{pmatrix}1&m&v_{1}\\0&1&0\\0&0&1\end{pmatrix}}$

haben. (Der Verschiebungsanteil $v_{2}$ muss verschwinden, da sonst die Fixpunktgleichung keine Lösung hat.) Multipliziert man zwei dieser erweiterten Matrizen, so ergibt sich:

${\begin{pmatrix}1&m&v_{1}\\0&1&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}1&n&w_{1}\\0&1&0\\0&0&1\end{pmatrix}}={\begin{pmatrix}1&m+n&v_{1}+w_{1}\\0&1&0\\0&0&1\end{pmatrix}}$.

Daraus wird offensichtlich:

1. Die Verkettung zweier Scherungen mit parallelen Achsen ist wieder eine Scherung mit einer Achse, die parallel zu den ursprünglichen Achsen ist.
2. Die Menge der Scherungen mit Achsen in einer festen Richtung bildet eine abelsche Gruppe.
3. Die Gruppe wird erzeugt von der Gruppe der Scherungen mit einer festen Achse (aus der Parallelenschar) und der Gruppe der Verschiebungen parallel zu dieser Achse. Sie ist sogar das direkte Produkt dieser Gruppen.
4. Die Gruppe ist isomorph zur Gruppe der Parallelverschiebungen der Ebene (also letztlich zum zweidimensionalen Vektorraum über dem Grundkörper als abelsche Gruppe).

Scherungen in höherdimensionalen Räumen

Die speziellere Verallgemeinerung der Scherung im dreidimensionalen Raum „kippt“ einen (geeignet ausgerichteten) Quader nur in einer Richtung, so dass er 4 rechteckige Seitenflächen behält.

In einem $n$-dimensionalen Raum ist eine Scherung eine Affinität, die eine Fixpunkthyperebene hat und durch die alle nicht auf dieser Hyperebene liegenden Punkte in eine feste Richtung parallel zur Fixpunkthyperebene verschoben werden. Die Länge eines Verschiebungsvektors ist dabei wieder proportional zum Abstand von der Fixpunkthyperebene.

Die allgemeinere Form verwandelt einen Quader in ein Parallelepiped.

In der Abbildung rechts ist dargestellt, wie das Bild eines Quaders bei einer solchen Abbildung zu einem schiefen Prisma verformt wird, wenn die Grundseite (rot) in der Fixpunktebene liegt und die Scherung parallel zur Vorderseite (gelb) wirkt. Im Bild bleiben die rote und die hellblaue Seite und die jeweils gegenüberliegenden Seiten Rechtecke.

Die Verallgemeinerung auf höherdimensionale Räume ist aber in der Literatur nicht einheitlich. Als Scherung des $n$-dimensionalen Raumes wird auch allgemeiner jede Affinität bezeichnet, die eine Matrixdarstellung der Form

${\begin{pmatrix}I_{1}&M\\0&I_{2}\end{pmatrix}}$

zulässt (bei Wahl einer geeigneten Basis). Dabei sind $I_{1},I_{2}$ Einheitsmatrizen und $M$ ist eine beliebige Matrix. Bei einer solchen Scherung ist der fixierte Raum ein linearer Raum der Dimension $\mathop {\mathrm {rang} } (I_{1})\geq 1$ (s. Rang (Lineare Algebra)).

Die Abbildung rechts zeigt die Wirkung der allgemeineren Form einer Scherung auf einen Quader im dreidimensionalen Raum. Das gezeigte Parallelepiped ist durch eine solche Scherung aus einem Quader hervorgegangen. Das (orientierte) Volumen des Parallepipeds stimmt mit dem des ursprünglichen Quaders überein.

Beide Übertragungen des Begriffs Scherung in der ebenen Geometrie auf höhere Dimensionen beschreiben inhaltstreue Affinitäten, die einen mindestens eindimensionalen affinen Teilraum punktweise fest lassen. Jede Scherung eines $n$-dimensionalen Raumes im allgemeineren Sinn (mit einer Fixpunktgeraden) lässt sich als Hintereinanderausführung von (höchstens) $n-1$ Scherungen im spezielleren Sinn (mit je einer Fixpunkthyperebene) darstellen. Dabei enthalten alle Fixpunkthyperebenen der spezielleren Scherungen die Fixpunktgerade der allgemeineren. Gibt es in dem $n$-dimensionalen Raum ein Skalarprodukt und besitzt die verallgemeinerte Scherung die oben genannte Matrixdarstellung bezüglich einer Orthonormalbasis des Raumes, dann können für die speziellen Scherungen, aus denen die allgemeine zusammengesetzt wird, die Fixpunkthyperebenen orthogonal zueinander gewählt werden.

Scherstreckung

Eine Scherstreckung entsteht, wenn eine zentrische Streckung und eine Scherung nacheinander (in beliebiger Reihenfolge) ausgeführt werden. In der Ebene kann sie durch Wahl geeigneter Koordinaten auf die Normalform $A={\begin{pmatrix}a&1\\0&a\end{pmatrix}};\quad a\in \mathbb {R} \setminus \lbrace 0;1\rbrace$ gebracht werden (siehe den Hauptartikel Jordansche Normalform). Sie hat keine Achse (Fixpunktgerade), aber ein eindeutiges Zentrum (Fixpunkt). Wird zusätzlich noch eine Verschiebung ausgeführt, so entsteht wieder eine Scherstreckung, wobei sich das Zentrum ändern kann.

Zusammenhang mit dem Begriff Scherung in der Mechanik

In der Mechanik, speziell der Kontinuumsmechanik bezeichnet man als Scherung bestimmte Verformungen eines dreidimensionalen Körpers. Dabei werden Massenelemente des Körpers in eine gemeinsame Richtung parallel zu einer festen Ebene im Körper verschoben und die Länge des Verschiebungsvektors ist proportional zum Abstand des Massenelementes von der festen (Fixpunkt-)Ebene. Der Begriff deckt sich also (als Abbildung) mit der spezielleren Verallgemeinerung auf drei Dimensionen, die weiter oben beschrieben ist. Wählt man das Koordinatensystem so, dass die unverschobene Ebene die xy-Ebene des kartesischen Koordinatensystems bildet und alle Verschiebungen parallel zur x-Achse erfolgen, dann lässt sich die dreidimensionale Scherung durch die lineare Abbildung

${\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}x+\Delta x\\y\\z\end{pmatrix}}={\begin{pmatrix}1&0&m\\0&1&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}x\\y\\z\end{pmatrix}}$

beschreiben. Dabei ist $\Delta x=m\cdot z$ die Verschiebung eines Massenelementes im Abstand $z$ von der Fixpunktebene. Ausgeführt wird dies im Hauptartikel Scherung (Mechanik).

Literatur

• H. Schupp: Elementargeometrie. UTB Schöningh, 1977, ISBN 3-506-99189-2, S. 150. 
• Hermann Schaal: Lineare Algebra und analytische Geometrie. 2. Auflage. Vieweg, Braunschweig 1980 (3 Bände: ISBN 3129228217, ISBN 3528130571, ISBN 3-528-13058-X). 

Weblinks

• Scherung in der Encyclopedia of Mathematics (engl.)